ADM形式のアフィン係数

ADM形式のアフィン係数

トビラ．． さんの書込 (2009/04/07(Tue) 02:27)

重力の正準理論のことについてなのですが，（多分ADM形式のところかな？）勉強していて，本に書いているところと僕の計算した結果が違って困っているのでどうか，アドバイス，ご指摘お願いします．まず，下準備として

\ast ギリシャ字を０〜４までをとるものとし，ラテン字を１〜３までの数字を取るものとします．

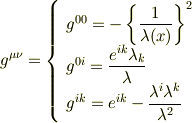
g^{\mu\nu}=\left\{ \begin{array}{l}g^{00}=-\left\{ \displaystyle\frac{1}{\lambda(x)}\right\}^2\\g^{0i}=\displaystyle\frac{e^{ik}\lambda_k}{\lambda}\\g^{ik}=e^{ik}-\displaystyle\frac{\lambda^i\lambda^k}{\lambda^2}\end{array}\right.
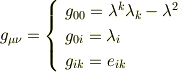
g_{\mu\nu}=\left\{ \begin{array}{l}g_{00}=\lambda^k \lambda_k-\lambda^2\\g_{0i}=\lambda_i\\g_{ik}=e_{ik}\end{array}\right.

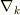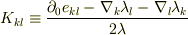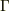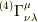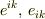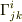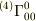ここで，３次元空間の共変微分を単に \nabla_k と書くことにして K_{kl}\equiv \displaystyle\frac{\partial _0 e_{kl}-\nabla_k\lambda _l -\nabla _l\lambda_k}{2\lambda} と定義して，また，４次元のアフィン係数 \Gamma を ^{(4)}\Gamma^\mu_{\nu\lambda} と書くことにして， e^{ik},\,e_{ik} から作られる３次元空間成分のアフィン係数を単に \Gamma^i_{jk} と書くことにします． そのようにすると，この本では例えば， ^{(4)}\Gamma^0_{00} は，

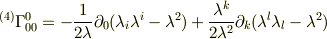
^{(4)}\Gamma^0_{00}=-\displaystyle\frac{1}{2\lambda}\partial_0(\lambda_i\lambda^i-\lambda^2)+\displaystyle\frac{\lambda^k}{2\lambda^2}\partial _k(\lambda^l\lambda_l-\lambda^2)

となっているのですが，僕が計算するとそのようにはどうしてもならず

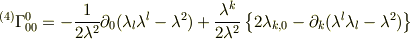
^{(4)}\Gamma^0_{00}=-\displaystyle\frac{1}{2\lambda^2}\partial _0(\lambda_l\lambda^l-\lambda^2)+\displaystyle\frac{\lambda^k}{2\lambda ^2}\left\{ 2\lambda_{k,0}-\partial _k(\lambda ^l\lambda_l-\lambda^2)\right\}

となるんです．どうしてこのように計算結果が食い違うのか疑問でたまりません． どうかどうか助言をお願いします．