線積分の計算法と内積の本質
線積分の計算法と内積の本質
数学迷い人↓ さんの書込 (2009/04/05(Sun) 13:56)
xy面上の円C:x^2+y^2=1にそっての,ベクトルA=(x^2+y,x^2+2z,2y)の線積分 ∫A・drを直接に計算するには,どのように進めればいいのですか? 最初の方の途中式だけでも構いませんので,教えてください.
あと,内積についてですが,スカラー倍ということで,普通の掛け算と同じに考えていいのでしょうか?だとしたら,内積の記号・を使わずにABなどと表記できますか? もちろん外積は特殊と心得ていますが.
Re: 線積分の計算法と内積の本質
Yokkun さんのレス (2009/04/05(Sun) 14:31)
こんにちは.
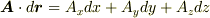 ですから,これにそのまま積分記号をつければいいのです.
ですから,これにそのまま積分記号をつければいいのです.
内積とスカラー倍は違いますよね?中央ドットを取ってしまうと直積(テンソル積)の意味として使う場合もあるようなので取ってはいけないと思います.
Re: 線積分の計算法と内積の本質
数学迷い人↓ さんのレス (2009/04/05(Sun) 15:03)
ありがとうございます. ということは,
計算すると,(1/3)x^3+x^2y+xy+4yz で合っていますか?
何度もすみません.
A(B・C)=(A・B)Cは成り立たないということですか?
Re: 線積分の計算法と内積の本質
リモコン さんのレス (2009/04/05(Sun) 15:37)
ベクトルの線積分は,「滑らかな曲線 C の接方向へベクトル場Aを積分すること」 です. (1/3)x^3+x^2y+xy+4yzはどのように計算しましたか?
一応普通に計算すると,(Cに沿って反時計回りに一周する積分ととらえています)
円C上の点  をパラメータtを用いて
をパラメータtを用いて
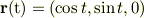
で表すと,点P上のベクトル 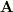 は
は
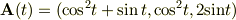
また, 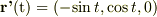 であるので,あとは高校の積分問題と同じです.
であるので,あとは高校の積分問題と同じです.
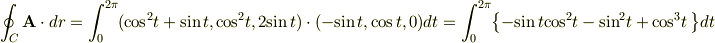
あとは計算頑張ってください.
内積についてはベクトルの内積は(ベクトル)・(ベクトル)=(スカラー)というスカラーを作る演算ですので,三つのベクトルからスカラーを作る演算ではありません ※スカラー3重積は三つのベクトルからスカラーを作る演算です. 三つのベクトルにたいして・を内積,×を外積とすると
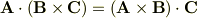
は成り立ちます
Re: 線積分の計算法と内積の本質
数学迷い人↓ さんのレス (2009/04/05(Sun) 16:16)
なるほどです.計算法はわかりました.ありがとうございます.
最後に,∫A・drというのは,内積を意味しているのですか?
もし,そうなら,drがベクトルというのが実感ができないです.drは微分記号ですよね?
何度も何度も,わからずやですみません↓
Re: 線積分の計算法と内積の本質
リモコン さんのレス (2009/04/05(Sun) 18:38)
はい,A・drの・は内積記号を表します.
曲線C上の位置ベクトルを  をパラメータ(媒介変数)として
をパラメータ(媒介変数)として 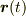 とします.
とします.
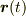 と,tがdtだけ微小変化した
と,tがdtだけ微小変化した 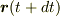 との差を表すベクトル
との差を表すベクトル 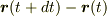 を
を 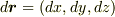 とします.(ベクトルの増分とでも言うのでしょうか,厳密に扱っていませんのでご了承を.)
ベクトル
とします.(ベクトルの増分とでも言うのでしょうか,厳密に扱っていませんのでご了承を.)
ベクトル 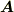 の任意の方向の成分はその方向の単位ベクトル
の任意の方向の成分はその方向の単位ベクトル  との内積
との内積 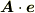 で表せるのはご存じかと思います.
曲線C
で表せるのはご存じかと思います.
曲線C 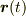 の接線方向の単位ベクトル
の接線方向の単位ベクトル  は
は
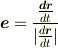
となります. 線積分は∫(ベクトル場の曲線Cの接線成分)(線素|dr|)ですので
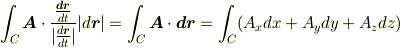
となるのです.
Re: 線積分の計算法と内積の本質
mNeji さんのレス (2009/04/05(Sun) 18:39)
横から失礼します.アスキー文字だけでヴェクタを表示するのは難しいですよね.
位置ヴェクタを成分表示として,
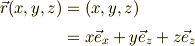
と書くとき,
この位置, 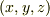 から微分量だけ離れた位置ヴェクタを
から微分量だけ離れた位置ヴェクタを 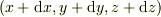 とする時,位置ヴェクタの全微分(微小変位ヴェクタ)を,
とする時,位置ヴェクタの全微分(微小変位ヴェクタ)を,
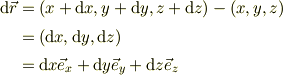
と書く事とします.
そう言う意味で,微小変位ヴェクタ 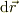 は位置の関数である普通のヴェクタ,
は位置の関数である普通のヴェクタ,
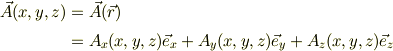
とのヴェクタ演算ができることになります.
【追記】
ここで, 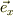 は,x軸方向の単位ヴェクタを意味します.座標系Oxyzは直交座標とすれば,各単位ヴェクタ相互の内積は;
は,x軸方向の単位ヴェクタを意味します.座標系Oxyzは直交座標とすれば,各単位ヴェクタ相互の内積は;
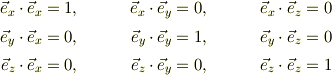
となります.
従って,ある位置ヴェクタ, 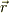 にある質点に,外力,
にある質点に,外力, 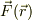 が加わって,その質点が微小変位,
が加わって,その質点が微小変位, 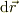 を起こした場合,外力が質点にする微小仕事は;
を起こした場合,外力が質点にする微小仕事は;
![\mathrm{d}W &= \vec F(\vec r) \cdot \mathrm{d}\vec r\\&= \left( F_x (x,y,z)\vec e_x +F_y (x,y,z)\vec e_y +F_z (x,y,z)\vec e_z \right) \cdot \left( \mathrm{d}x\vec e_x + \mathrm{d}y\vec e_y +\mathrm{d}z\vec e_z \right)\\&= F_x (x,y,z)[\vec e_x \cdot \left( \mathrm{d}x\vec e_x + \mathrm{d}y\vec e_y +\mathrm{d}z\vec e_z \right)]\\&\quad +F_y (x,y,z)[\vec e_y \cdot \left( \mathrm{d}x\vec e_x + \mathrm{d}y\vec e_y +\mathrm{d}z\vec e_z \right)]\\&\quad +F_z (x,y,z)[\vec e_y \cdot \left( \mathrm{d}x\vec e_x + \mathrm{d}y\vec e_y +\mathrm{d}z\vec e_z \right)]\\&= F_x (x,y,z)[\mathrm{d}x \vec e_x \cdot \vec e_x + \mathrm{d}y\vec e_x \cdot \vec e_y +\mathrm{d}z\vec e_x \cdot \vec e_z]\\&\quad +F_y (x,y,z)[\mathrm{d}x \vec e_y \cdot \vec e_x + \mathrm{d}y\vec e_y \cdot \vec e_y +\mathrm{d}z\vec e_y \cdot \vec e_z]\\&\quad +F_z (x,y,z)[\mathrm{d}z \vec e_z \cdot \vec e_x + \mathrm{d}y\vec e_z \cdot \vec e_y +\mathrm{d}z\vec e_z \cdot \vec e_z]\\&= F_x (x,y,z)[\mathrm{d}x*1 + \mathrm{d}y*0 +\mathrm{d}z*0]\\&\quad +F_y (x,y,z)[\mathrm{d}x *0 + \mathrm{d}y*1 +\mathrm{d}z*0]\\&\quad +F_z (x,y,z)[\mathrm{d}z *0 + \mathrm{d}y*0 +\mathrm{d}z*1]\\&= F_x (x,y,z)\mathrm{d}x +F_y (x,y,z)\mathrm{d}y +F_z (x,y,z)\mathrm{d}z](http://hooktail.maxwell.jp/bbslog/c4d12fef2154eacd5996d7df179ff874.png)
となります.これだけの面倒な計算を,ヴェクタ表現によって短く出来ているのには驚きますね
Re: 線積分の計算法と内積の本質
toorisugari no Hiro さんのレス (2009/04/06(Mon) 10:47)
> ∫A・drというのは,内積を意味しているのですか?
リモコンさんの説明で十分ですが,まだ,イメージがつかないなら,
曲線を折れ線で近似して,
曲線C上の線積分 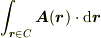 を,
折れ線上での内積の総和
を,
折れ線上での内積の総和 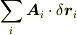 だと
考えればいいのです.
#
だと
考えればいいのです.
# 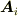 は線分
は線分 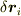 の中点における
の中点における 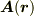 です.
です.
線分を細かく取っていけば,折れ線は曲線に近づきます.そのとき, 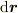 は十分微小な
は十分微小な 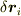 と思えばよいのです.
と思えばよいのです.
Re: 線積分の計算法と内積の本質
数学迷い人↓ さんのレス (2009/04/09(Thu) 09:51)
やっと計算できました.今までありがとうございます.
次は,これをストークスの定理により面積分に変換して計算してみたいのですが,
元の問題: xy面上の円C:x^2+y^2=1にそっての,ベクトルA=(x^2+y,x^2+2z,2y)の線積分 ∫A・drを計算する.
∬(0,0,2x-1)・ndS とやっていったのですが,ここまで合っていますか? また,この先の計算の仕方がわからないのですが,教えて頂けないでしょうか?
Re: 線積分の計算法と内積の本質
ASA さんのレス (2009/04/09(Thu) 11:24)
xy面単位円領域の積分だから,円筒座標系で計算するときっと簡単になるはず. ∬Bz(x,y,z)dS->∬B(r,θ,z)r dr dθ[r:0〜1,θ:0〜2π]