rotA

rotA

ハチ さんの書込 (2009/04/05(Sun) 13:30)

rotAを計算したら，（2x+2y,0,2x）という成分表示になったのですが， これをさらに，まとめて・・・

答えは，rotA=4x+2yという風に足し合わせて良いのでしょうか？

下らない質問と思いますが，お願いします．

Re: rotA

リモコン さんのレス (2009/04/05(Sun) 14:24)

回転（rot）はベクトルに作用してベクトルをつくります． ですから rotA=（2x+2y,0,2x） が答えとなります．足しあわせてはいけません．

Re: rotA

ハチ さんのレス (2009/04/05(Sun) 15:07)

回答ありがとうございます．

では，divAの計算結果は，成分表示ではなくて，数式ですよね？

Re: rotA

リモコン さんのレス (2009/04/05(Sun) 15:48)

そのとうりです． div(ベクトル)＝（スカラー） です

Re: rotA

ハチ さんのレス (2009/04/06(Mon) 13:41)

わかりました．

では，外積の計算

C=A×Bは成分表示にしてから，それらを足すことは可能ですよね？

Re: rotA

toorisugari no Hiro さんのレス (2009/04/06(Mon) 14:58)

> C=A×Bは成分表示にしてから，それらを足すことは可能ですよね？

？？？

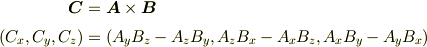
\bm{C}&=\bm{A}\times\bm{B}\\(C_x,C_y,C_z)&=(A_yB_z-A_zB_y,A_zB_x-A_xB_z, A_xB_y-A_yB_x)

で打ち止めです．

(A_yB_z-A_zB_y)+(A_zB_x-A_xB_z)+(A_xB_y-A_yB_x)

にあたるのは

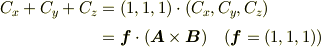
C_x+C_y+C_z &=(1,1,1)\cdot(C_x,C_y,C_z)\\&=\bm{f}\cdot(\bm{A}\times\bm{B}) \quad (\bm{f}=(1,1,1))

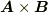であって， \bm{A}\times\bm{B} ではないですね．

Re: rotA

リモコン さんのレス (2009/04/06(Mon) 15:22)

回転を作用させる行為と同様，ベクトルどうしの外積の結果もベクトルになります． toorisugari no Hiroさんの回答のとうりです．

外積の性質としては

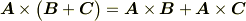
\bm{A} \times \bigl(\bm{B} +\bm{C} \bigr)=\bm{A}\times \bm{B} +\bm{A}\times \bm{C}
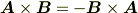
\bm{A}\times \bm{B}=-\bm{B}\times \bm{A}

などです． ちなみに結合法則は成立しないですよ．

ベクトルの演算については，「物理のかぎしっぽ」やその他いろいろなサイトで紹介されているかと思います．そちらを参照することをオススメします．

Re: rotA

ハチ さんのレス (2009/04/06(Mon) 15:22)

ベクトル（外積）では，成分表示までで， スカラー（内積など）では，成分表示から，数式に表現できるという解釈でいいでしょうか？

Re: rotA

toorisugari no Hiro さんのレス (2009/04/06(Mon) 15:34)

> 数式に表現できるという解釈でいいでしょうか？

「数式」というのが意味不明です．実数あるいはスカラーならわかりますが．

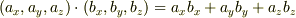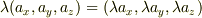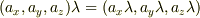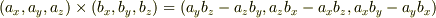内積: ベクトル \cdot ベクトル -> スカラー (a_x,a_y,a_z)\cdot(b_x,b_y,b_z)=a_xb_x+a_yb_y+a_zb_z スカラー倍: スカラー ベクトル -> ベクトル \lambda (a_x,a_y,a_z)=(\lambda a_x, \lambda a_y, \lambda a_z) スカラー倍: ベクトル スカラー -> ベクトル (a_x,a_y,a_z)\lambda =(a_x\lambda, a_y \lambda, a_z \lambda) ベクトル積: ベクトル \times ベクトル -> ベクトル (a_x,a_y,a_z)\times(b_x,b_y,b_z)=(a_yb_z-a_zb_y, a_zb_x-a_xb_z, a_xb_y-a_yb_x) が基本で，あとはこの組み合わせです．