微分表記

微分表記

名前はまだない．．． さんの書込 (2009/04/04(Sat) 23:54)

ｒ=(rcosθ)i+(rsinθ)j

を微分せよとあるのですが，

dr=.... と始まっています．

微分は，dr/dθのような形ではないのでしょうか？

しばしば，微分以外でも，dを頭に表記しているのを目にしますが，微分とは意味が違ってくるのでしょうか？

よろしければ，お手数ですが回答お願いいたします．

Re: 微分表記

Yokkun さんのレス (2009/04/05(Sun) 07:02)

名前はまだない．．．さん，おはようございます．

厳密な定義はさておき，微分記号d はもともと変化を表す?とほぼ同じで，その無限小極限と考えることができると思います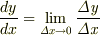． \frac{dy}{dx}=\lim_{{\it\Delta}x\rightarrow 0}\frac{\it{\Delta}y}{\it{\Delta}x} すると，y(x)の微小な変化?yは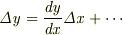， \it{\Delta}y=\frac{dy}{dx}\it{\Delta}x+\cdots と書けます．無限小の極限で 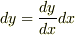dy=\frac{dy}{dx}dx とすれば，微分記号の分母分子を切り離して形式的に「約分」できるという便利さが生じるわけです．二変数関数では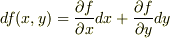， df(x,y)=\frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy と書けることになります．この形式をf(x,y)の全微分といいます．

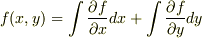
全微分は，積分記号をつければそのまま積分の形式ができあがるので便利です． f(x,y)=\int \frac{\partial f}{\partial x}dx + \int \frac{\partial f}{\partial y}dy

Re: 微分表記

名前はまだない．．． さんのレス (2009/04/06(Mon) 15:38)

ご丁寧にありがとうございます．しかし，

?とδとdの区別がよくわからないのですが・・・

Re: 微分表記

Yokkun さんのレス (2009/04/07(Tue) 10:35)

>?とδとdの区別がよくわからないのですが・・・

私も厳密な定義はわかりません．本来は「変化」を意味する同源の記号でしょうから，同じように使われることもあるようです．しかし，一般的によくみかける用法としては， ?＝有限の変化量（差分） δ＝関数においてあるパラメータが変化した（関数自体が変化した）ときの関数値の変化量（変分） d＝無限小の変化量（?の極限） という使い分けが多いと思います．下記Ｑ＆Ａなど参考になりましたら．

Re: 微分表記

toorisugari no Hiro さんのレス (2009/04/07(Tue) 10:47)

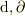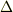Yokkunさんの説明以上の厳密な定義はたぶんない( \mathrm{d}, \partial は別ですが)と思いますので，文脈で理解するのが良いと思います．いろいろな使い方を，意味を考えながら，手を動かしていけば，理解できると思います． # ちなみにΔあるいは \Delta の事でしょうが，私の端末では?にしか見えません．機種依存文字でしょうね．

Re: 微分表記

Yokkun さんのレス (2009/04/07(Tue) 18:12)

>機種依存文字でしょうね．

不用意に使ってしまいました．申しわけありません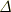． \it{\Delta} です．Δはラプラシアンに見えるので斜体を使ったつもりでしたが不覚でした．

Re: 微分表記

mNeji さんのレス (2009/04/07(Tue) 20:37)

＞>機種依存文字でしょうね．

「Windows XP」と「Mac OS X 10.4」とから，両者ともFirefox3.0.8で見ていますが，問題なく見えています．

〜〜〜〜 名前はまだない．．．さん，敢えて形式的な算法を示してみたいと思います．

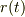元のご質問について，位置ヴェクタを極座標で表現したと考えた場合の計算から出発したいと思います．ある時刻 t の時に，原点からの距離 r(t) と，x軸からの反時計方向にみた角度 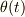\theta(t) とします．

\vec r(t) = r(t)[\cos(\theta(t))\vec e_x + \sin(\theta(t))\vec e_y ]

両辺を時間で微分しますと，

\frac{\mathrm{d}\vec r(t)}{\mathrm{d} t}&= \frac{\mathrm{d}\{r(t)[\cos(\theta(t))\vec e_x + \sin(\theta(t))\vec e_y]\} }{\mathrm{d} t}\\&= \frac{\mathrm{d} r(t)}{\mathrm{d} t}[\cos(\theta(t))\vec e_x + \sin(\theta(t))\vec e_y] +r(t)\frac{\mathrm{d}}{\mathrm{d} t}[\cos(\theta(t))\vec e_x + \sin(\theta(t))\vec e_y] \\&= \frac{\mathrm{d} r(t)}{\mathrm{d} t}[\cos(\theta(t))\vec e_x + \sin(\theta(t))\vec e_y] +r(t)\frac{\mathrm{d} \theta(t)}{\mathrm{d}t}\frac{\mathrm{d}}{\mathrm{d} \theta}[\cos(\theta)\vec e_x + \sin(\theta)\vec e_y]\\&= \frac{\mathrm{d} r(t)}{\mathrm{d} t}[\cos(\theta(t))\vec e_x + \sin(\theta(t))\vec e_y] +r(t)\frac{\mathrm{d} \theta(t)}{\mathrm{d}t}[-\sin(\theta)\vec e_x + \cos(\theta)\vec e_y]

となりますね．で，両辺に 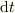\mathrm{d} t を掛けると考えると如何でしょうか？

\mathrm{d}\vec r = [\cos(\theta)\vec e_x + \sin(\theta)\vec e_y] \mathrm{d} r + r(t)[-\sin(\theta)\vec e_x + \cos(\theta)\vec e_y]\mathrm{d} \theta

Re: 微分表記

toorisugari no Hiro さんのレス (2009/04/07(Tue) 21:40)

> 機種依存文字でしょうね．

CentOSでも大丈夫だったんで，私の端末のFirefoxのFont設定の問題のようです．お騒がせてしてすいません．