"△"ラプラス,ポアソン,そして波動方程式へ
"△"ラプラス,ポアソン,そして波動方程式へ
リモコン さんの書込 (2009/04/01(Wed) 16:41)
こんにちは,以前包絡線について,質問させていただいたリモコンです. 以前の質問で議論していただきありがとうございました.理解できました. 自分も今学期から高校3年生.受験になります.
今回はタイトルどうり,ラプラシアン"△"が使われている方程式について質問させていただきます. △f,というようにラプラシアンを作用させた関数の表す意味は,いろいろなサイトを見て回ってみて『ある点の周りの関数の値の平均値とある点の関数の値の差を表す』というイメージがつかめました.
そのことからラプラス方程式,およびポアソン方程式のイメージも何となくつかめましたし,実際にラプラス方程式を満たす関数をグラフで表すと,たとえばx方向の曲がり具合(二次偏微分)とy方向の曲がり具合がたがいに打ち消しあっている様子などが見て取れたり, 電荷密度ρの球の内側と外側の電位φの△φがそれぞれ-ρ/εと0になるのも計算で確認できたときは感動しました.
この調子で今度は"波動方程式"の表している意味をイメージしてみようと思ったのですが,どうもイメージできません,
*どなたか波動方程式の表す意味についてアドバイスをくださる方がいらっしゃったらお願いします.
*あと,ラプラシアンを作用させた関数の表す意味を"△は勾配の発散"という角度から眺めてイメージをつかむ方法,手助けとなるサイトなどを知っていたらぜひ教えて下さい.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
toorisugari no Hiro さんのレス (2009/04/01(Wed) 18:33)
あまり,アドバイスできることはなさそうですが...
> "波動方程式"の表している意味をイメージしてみようと思ったのですが,どうもイメージできません
それは一次元の波動方程式
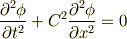
のイメージができないと言うことですか?それとも,一次元は分かるが

のイメージができないと言うことですか?
Re: "△"ラプラス,ポアソン,そして波動方程式へ
リモコン さんのレス (2009/04/01(Wed) 20:06)
ご回答ありがとうございます一次元の波動については自分なりの式の意味を考えております.
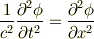
の波動の速度cを∂記号の中に入れて
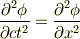
とし,この式を"xとφをそれぞれ軸にとったときのφの曲がり具合(どのくらい上に凸または下に凸か)が,ctとφをそれぞれ軸にとったときの曲がり具合が等しくなる"という理解です. 一次元でもっとわかりやすいイメージがあったら是非教えていただきたいです.
二次元,三次元の波動方程式のイメージはつかめていません.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
toorisugari no Hiro さんのレス (2009/04/01(Wed) 20:27)
> "xとφをそれぞれ軸にとったときのφの曲がり具合(どのくらい上に凸または下に凸か)が,ctとφをそれぞれ軸にとったときの曲がり具合が等しくなる"
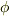 を弦の振幅とみると,
を弦の振幅とみると, 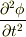 はある点
はある点  における弦の振動の「加速度」と考えられます.右辺
における弦の振動の「加速度」と考えられます.右辺 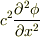 は,弦がどれだけ曲がっているかに比例するので,単位質量あたりの「(まっすぐになるための)復元力」と考えられます.
は,弦がどれだけ曲がっているかに比例するので,単位質量あたりの「(まっすぐになるための)復元力」と考えられます.
# 格子点での値  を使って2階微分を差分化すれば,
を使って2階微分を差分化すれば,
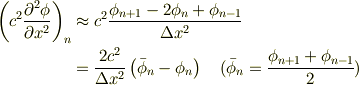
「周りの平均からのズレをうち消す様に復元力が発生する」と解釈できます.
ただ,これだと,一点における単振動的振る舞いはイメージできても,波が伝わる様子はイメージできませんね.
ダランベールのやり方にそって
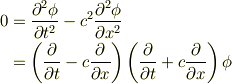
と因数分解し,
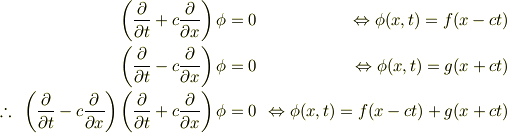
とやるしかなさそうです.( 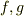 は任意関数)
は任意関数)
元の
> "xとφをそれぞれ軸にとったときのφの曲がり具合(どのくらい上に凸または下に凸か)が,ctとφをそれぞれ軸にとったときの曲がり具合が等しくなる" に近いイメージができるのは

"  と
と  をそれぞれ軸にとったときの
をそれぞれ軸にとったときの  の 「傾き」が,
の 「傾き」が, 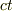 と
と 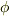 をそれぞれ軸にとったときの「傾き」のマイナスに等しくなる"
=
"(傾きベクトルは等高線に垂直だから)
をそれぞれ軸にとったときの「傾き」のマイナスに等しくなる"
=
"(傾きベクトルは等高線に垂直だから) 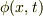 の等高線は
の等高線は 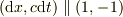 というベクトルに垂直である.つまり,等高線は
というベクトルに垂直である.つまり,等高線は 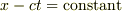 となる."
でしょうか.
となる."
でしょうか. 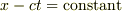 となる直線のことを「特性曲線」といいます.
となる直線のことを「特性曲線」といいます.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
mNeji さんのレス (2009/04/04(Sat) 12:40)
横から失礼します.
私は,波動方程式の微分幾何的なイメージを理解出来ない者です.ただ波動方程式,

について,学部1年のときに悩んだ事があるのでコメントします.
toorisugari no Hiroさんの仰る,
>ダランベールのやり方にそって
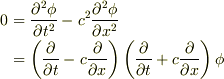 >と因数分解し,
>と因数分解し,
までは良いと思います.この因数分解をする事ができるのは,偏微分の順番は交換出来ることを利用していますね.
当時,それから先が「?」でした.一時は,強引に,

としてもしっくり来なかったです.
数学ができる親友に話した所,変数変換の方法を教えて貰いました.以下に,そのあらすじを書きます.
2つの変数, 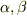 について,線形変換を考える.
について,線形変換を考える.

同時に,波動量 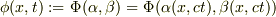 と読み替える.
と読み替える.
そこで,波動量についての 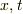 を
を 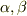 に書き換える事を考えれば,式(1)を用いて,
に書き換える事を考えれば,式(1)を用いて,
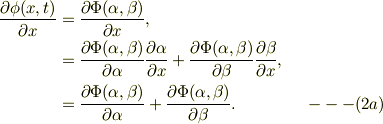
同様に,
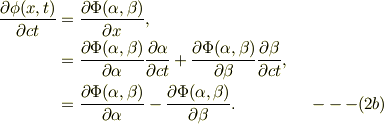
式(2a),(2b)の辺々の和,差を取れば,
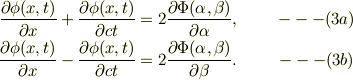
従って,波動方程式(0)は,
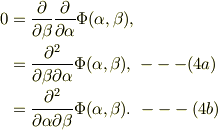
式(4a)から, 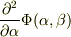 は
は  の関数ではないので,
の関数ではないので,  だけの関数,
だけの関数, 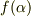 である.同様に,式(4b)から
である.同様に,式(4b)から  がえられる.一般には,両者の和が波動量となる.
がえられる.一般には,両者の和が波動量となる.
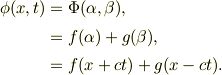
といった流れだったとおもいます.「t=0」の解が,時間にともなって,左右に分かれていくイメージには驚きましたね.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
ASA さんのレス (2009/04/04(Sat) 15:22)
mNejiさん これまた本題とは関係ない突っ込みですが, >「t=0」の解が,時間にともなって,左右に分かれていくイメージには驚きましたね. φ(x,t)=Cxtも解ですが,左右に分かれていくイメージにはなりませんよね.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
mNeji さんのレス (2009/04/04(Sat) 17:36)
ASAさん,
>φ(x,t)=Cxtも解ですが,左右に分かれていくイメージにはなりませんよね.
なるほど,不思議な解ですね.t=0では,波動が無いのに,一寸時間が経つと,無限大までにまで急上昇する訳ですか.何かの付帯条件,ある領域について限定とかが付いて,意味のある解になるのでしょうか?
Re: "△"ラプラス,ポアソン,そして波動方程式へ
toorisugari no Hiro さんのレス (2009/04/04(Sat) 18:39)
> φ(x,t)=Cxtも解ですが,左右に分かれていくイメージにはなりませんよね.
ま,それを言ったら定在波も左右に分かれていくようには見えませんがね.:-) # こっちは単振動でイメージできるからかえって都合がいいですが.
でもきっと,見る人が見ると
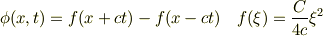
と,左右に分かれていく波(?)が見えるんでしょうね.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
toorisugari no Hiro さんのレス (2009/04/04(Sat) 19:13)
> それから先が「?」でした.
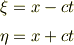
より,微分の鎖則と逆行列により,
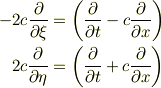
とするのが標準的ですが,
フーリエ変換
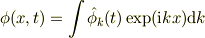
を使って
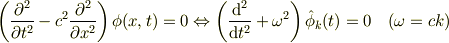
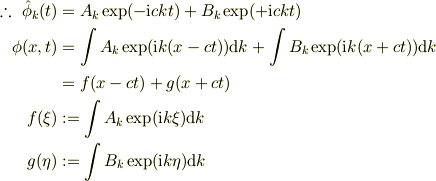
とするやり方もありますね.(初学者むきでは当然ないです.)
Re: "△"ラプラス,ポアソン,そして波動方程式へ
ASA さんのレス (2009/04/04(Sat) 19:15)
偏微分方程式には,物理的に意味の無い解も包含されるという注意です.
>定在波も左右に分かれていくようには見えませんがね でも,定在波は物理的解釈は可能ですよね.
φ(x,t)=Cxtでこれを横波と無理に解釈すると,t=0でx軸と一致している自由端の弦が無限大の時間をかけて回転し,最終的にy軸に一致すると解釈できますが,しかし,元の力学的運動方程式からでは,加速度が常に0のケース相当するので,等速回転運動するはずです.このような矛盾が生じる解です.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
toorisugari no Hiro さんのレス (2009/04/04(Sat) 19:37)
> 偏微分方程式には,物理的に意味の無い解も包含されるという注意です.
なるほど.ただ,
> 加速度が常に0のケース相当するので,等速回転運動するはずです.
はちょっと分かりません.並進加速度は0ですが,これが回転加速度とどうつながるのでしょうか?
Re: "△"ラプラス,ポアソン,そして波動方程式へ
ASA さんのレス (2009/04/04(Sat) 20:27)
>並進加速度は0ですが,これが回転加速度とどうつながるのでしょうか? 暗黙の前提として,弦の長さを拘束条件としたからです. 現実問題,幾らでも伸びる物体って存在しないでしょ. そもそも微小変位の考察で得られた方程式ですからね. 横変位が微小なら,回転角も微小で比例していると考えられるので(tanθ=θ),その範囲では,回転との解釈も可能でしょ.
もっとも,φを円周方向変位と看做せるなら,そのまま任意角速度での回転運動との解釈が可能ですけどね.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
toorisugari no Hiro さんのレス (2009/04/04(Sat) 20:48)
> 暗黙の前提として,弦の長さを拘束条件としたからです.
??? やっぱり,回転加速度にむすびつけられないですが.
> 現実問題,幾らでも伸びる物体って存在しないでしょ.
グローバルにみると,そうかもしれませんが,局所的にみればあまりおかしく感じません.
そもそも,それを言うなら,初速度が無限遠方で発散している事が不自然だと言う方が納得できます.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
ASA さんのレス (2009/04/04(Sat) 21:06)
>初速度が無限遠方で発散している事が不自然だと言う方が納得できます. 有限長自由端の弦を考えるなら,問題ありません. この場合,弦の外側の速度を云々すること自体が不適切となります.
物理的状況と,境界条件とのすり合わせが物理の醍醐味でもありますね.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
通りすがりのひろ さんのレス (2009/04/04(Sat) 21:51)
# toorisugari no Hiro@携帯です.
局所的見方を許してもらえるなら,そもそも,問題の解は, 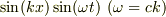 を長波長の仮定
を長波長の仮定 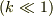 のもと,
のもと, 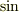 の一次関数近似
の一次関数近似
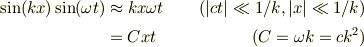
したものですよね.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
mNeji さんのレス (2009/04/05(Sun) 08:14)
亀レスのようですが,
定義,

から,
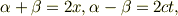
ですから,
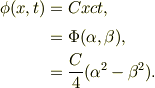
形式的には,方向が逆の関数の差で表せますね.
#toorisugari no HiroさんのNo.23316と同じでしたが....
>偏微分方程式には,物理的に意味の無い解も包含されるという注意です.
今回の事例が意味が在る為の条件はあるのでしょうか.
他にも実例があれば,お教え下さい.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
ASA さんのレス (2009/04/05(Sun) 09:11)
一般解がφ=f(α)+g(β)です. f,gが遠方で0収束なら,波束の考えで解釈可能です. 0収束しないケースとしてf,gをα,βの冪展開で考えます.冪n=1のときは φ_x=A(α+β)=Cx,φ_t=A(α-β)=Ct φを電位と見ると,φ_xは一定勾配,つまり電場強度がCである定電場を示していると解釈できます.一方φ_tは,電位が速度Cで変化している状態と解釈できますが,物理的に意味のある状態としては,φをベクトルポテンシャルと見ることで同様に定電場を示していると解釈できます. 冪nが2以上だと,解釈が難しくなります. φ=A(α^2-β^2)は,先に示したように有限長の弦の回転というちょっとアクロバティックな解釈が可能でしたが,φ=A(α^2+β^2)=B(x^2+(ct)^2)になると解釈は思いつきませんでした.もしかしたら,面白い解釈が可能かもしれません.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
yama さんのレス (2009/04/05(Sun) 10:10)
左右に分かれていくイメージというのは,左右に分かれた波が単独に観察できる場合は分かりやすいのですが,そうでない場合はイメージしにくいですね. 例えば,パルス波のように有限区間だけを占める2つの波がある場合は,その波が重なってから分かれたあとは,2つの波をそれぞれ単独の波として観察できます. しかし,無限に続く2つの波の場合は,観察できるのは合成波のみであって,その合成波を構成する2つの波を別々に観察することはできません.定常波の場合も同様です. これらの場合も,式で表せば,左右に進む波の重ね合わせであることは分かりますね.
φ(x,t)=Cxt についても,toorisugari no Hiroさんが指摘されている通り,左右に進む波の重ね合わせと見なせますね. これは無限遠で発散するので無限区間の解としては不適切ですが,有限時間の間に有限区間でのみ限定的にこの形で表される解はあり得ます.
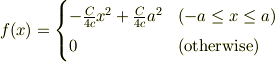
とすると, 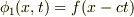 は,正の向きに進む幅2aの山からなるパルス波です.
同様に
は,正の向きに進む幅2aの山からなるパルス波です.
同様に
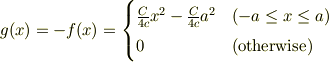
とすると, 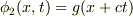 は,負の向きに進む幅2aの谷からなるパルス波です.
これらの合成波
は,負の向きに進む幅2aの谷からなるパルス波です.
これらの合成波 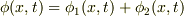 を考えると,2つのパルス波が左右から近づいてきて重なった後,再び左右に分かれることが分かります.
そして,2つのパルス波が重なっている間,重なっている区間に限れば
を考えると,2つのパルス波が左右から近づいてきて重なった後,再び左右に分かれることが分かります.
そして,2つのパルス波が重なっている間,重なっている区間に限れば 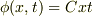 になることが分かります.
になることが分かります.
Re: "△"ラプラス,ポアソン,そして波動方程式へ
toorisugari no Hiro さんのレス (2009/04/09(Thu) 23:54)
その後レスポンスがなかったので続かなかったですが,
> *あと,ラプラシアンを作用させた関数の表す意味を"△は勾配の発散"という角度から眺めてイメージをつかむ方法,手助けとなるサイトなどを知っていたらぜひ教えて下さい.
について. ラプラシアンには「縦ベクトル横ベクトル」に絡む「双対ベクトル」という概念や「ホッジ双対」という「互いに直交する平面と直線を相互に入れ替える操作に相当する」概念が背景にあるので,幾何学的説明は難しいのですが,おおざっぱに作図的な説明をします.
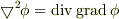
2次元で考えましょう.関数 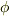 を等高線表示(3次元なら等値「面」表示)で作図したとします.そのときの間隔は十分細かいとします.
を等高線表示(3次元なら等値「面」表示)で作図したとします.そのときの間隔は十分細かいとします.
ある点で等高線群をみると,局所的には互いに平行な等間隔に並んだ直線群(3次元なら平面群)が得られます.これを「層ベクトル(双対ベクトル)」といいます. 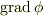 が表すのは通常の線ベクトルでなく層ベクトルです.(層ベクトルの大きさは間隔に反比例します.)
が表すのは通常の線ベクトルでなく層ベクトルです.(層ベクトルの大きさは間隔に反比例します.)
次に,「発散」を考えるために,ホッジ双対を取ります.等高線に垂直になるように曲線群を引きます.曲線と曲線との間隔は等高線とで作られる「格子が正方形に近くなる」ように作図します.できるだけ,つながった曲線群にしたいのですが,等高線の分布によっては,曲線は途中で消えたり,途中から発生したりと,「端点」が発生します.
3次元の場合には「格子が立方体に近くなる」ように曲線群を引いていくと,曲線の束ができます.この束には向きがあり,束の密度を大きさと考え,曲線の接線を方向と考えるとベクトルになります.これを「束ベクトル」といいます.
ホッジ双対 : 層ベクトル -> 束ベクトル (二つのベクトルは同じ向き,同じ方向,同じ大きさになります.)
等高線(面)には切れ目(端線?)はないです(rotgrad=0)が,束ベクトルには「端点」があります.この端点の密度が「束ベクトル(=層ベクトル)の発散」です.
つまり 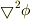 は端点の密度です.
は端点の密度です.
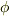 を静電ポテンシャル,層ベクトルを電場,束ベクトルを構成する一本の曲線を電気力線と考えれば,ガウスの法則により「端点」は電荷に相当することが分かると思います.
を静電ポテンシャル,層ベクトルを電場,束ベクトルを構成する一本の曲線を電気力線と考えれば,ガウスの法則により「端点」は電荷に相当することが分かると思います.
作図で 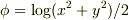 と
と 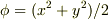 の場合で端点ができるかできないか試してみてください.(前者は原点以外の端点はありませんが,後者は一様に存在します.)
の場合で端点ができるかできないか試してみてください.(前者は原点以外の端点はありませんが,後者は一様に存在します.)