三輪次男 さんの書込 (2009/04/01(Wed) 10:10)

インタ−ネットで四次方程式の解を検索して勉強しております． その中の四次方程式の解法．四次方程式の解の公式 （４）式［y^2 + 1/2（B2 + t）］^2 〓 t（y - 1/2t.B1）^2 - 1/4t.B1^2 - B0 + 1/4（B2 + t）^2 この剰余項〓０とした （５）式-1/4t.B1^2 - B0 + 1/4（B2 + t）〓 0 整理した三次方程式t^3 + C2.t^2 + C1.t + C0 〓 0 解をt 〓 t1 ，t2 ，t3としておりますが この三次方程式の解と四次方程式の解との関係に どのような意味があるのでしょうか？教えてください

Yokkun さんのレス (2009/04/01(Wed) 17:08)

2乗＝2乗の形にむりやり変形させるのに，ひとまず を導入して目的の形になる をみつけているだけですね？

たとえば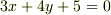， という方程式があったとして，これを 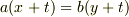の形にしようという目的があったとします．

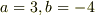はすぐにわかりますから，展開整理すれば 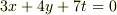最初の式と比べて

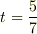
以上の論理の流れが理解できますか？

toorisugari no Hiro さんのレス (2009/04/01(Wed) 18:26)

本筋とは関係ない話です． 何故ゲタ記号を等号代わりに使われるのですか?ゲタ記号〓は「表示不可能文字」を表す写植用記号であり，数学記号である等号＝ではありません．このような文脈で使う文字ではないと思います．

下駄記号

• http://ja.wikipedia.org/wiki/%E4%B8%8B%E9%A7%84%E8%A8%98%E5%8F%B7

toorisugari no Hiro さんのレス (2009/04/08(Wed) 15:48)

こちらにつけておきます

> Yokkunさんのレスへの返礼No. 23301 に対して
> 数学の証明はしばしば，トリックを感じます．
> ありがとうございました． ::

> toorisugari no Hiro さんのレスへの返礼 > 私は，下駄記号は知りませんでした．〓 > 黒く，太くてアクセントがあると思ってつかいました． > おはづかしい次第です．ありがとうございました．

> 以前，質問を出したとき返礼ができるような書式であったように思います．
> 返信書式の画面はどうすればよいでしようか？
> 教えてください．

「返/修/削」ボタンを押して最後にある欄に記入するだけです．