名前はまだない さんの書込 (2009/03/29(Sun) 05:07)

こんにちは，高専の四年生です． ラグランジュの未定乗数法の復習のためにこのサイトの情報を参考にさせて 頂いてたのですが，計算力の不足のため困っています．

• http://www12.plala.or.jp/ksp/mathInPhys/lagrangeUndetermin/

このページの例題1ですが，3つの連立方程式を導くところまでは 理解できるのですが，この連立方程式からx,y,λを求めることができません． 3つの式に3つの未知数ですから求めることができるはずですが・・・．

1つの式にxとyが同時に存在してしまうためうまく解くことができません． 教科書・参考書などに載ってる典型問題ではxとyが同時に現れないので 楽に解くことができるのですが．

単純な計算力の問題だと思われますので恐縮ですが，これだけ解けないのも すごく悔しくて眠れないのでよろしくお願いします．

yama さんのレス (2009/03/29(Sun) 08:59)

最初の２つの式は，x,yについて連立一次方程式になっているので簡単に解けて，x,yをλの関数として表すことができます． それを３番目の式に代入すればλを求めることができます．

名前はまだない さんのレス (2009/03/29(Sun) 18:19)

素早いご対応どうもありがとうございます． しかし折角ながら未だに問題は解決できてません・・・．

x,yをλの関数であらわすということは 1番目の式を整理してy=λx/2a^2, 2番目の式を整理してx=λy/2b^2を導くということでしょうか．

これらを3番の式のxとyにそれぞれ代入しますと λ=(2(ab)^2)/√((ay)^2+(bx)^2)になると思いますが， これを用いてxの式とyの式からλを消去したいのですが どうしてもx=a/√2とy=b/√2が求まらなくて困っています．

根本的に間違ってましたらご指摘をどうか宜しくお願いします．

yama さんのレス (2009/03/29(Sun) 18:36)

最初の２式の右辺が0になっているのを見落としていました． この場合，x.yはこの２式からは一意的には決まらないので，上記の方法ではうまくいきませんね． x=y=0 が最初の２式を満たしますが，これは３番目の式を満たしません． 最初の２式が x=y=0 以外の解を持つためにはx,yの係数の行列式が0にならないといけないので，その条件からλが決まり，それを用いてx,yを決めることができます．

あるいは次のようにしてλを求めることもできます． y=λx/2a^2 に x=λy/2b^2 を代入すると

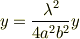
となるので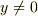， の場合は

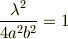
よりλが求められます．

名前はまだない さんのレス (2009/03/30(Mon) 23:31)

ご親切に教えて頂いてありがとうございます． お蔭様でラグランジュの未定乗数法を少しは理解することができました．

いろんな演習問題にも挑戦してみましたが 変数の多い関数だったり，複雑な関数の場合は 連立方程式の解を求めるのも大変ですね・・・．

もっと計算力をつけるべく頑張ります．