ペンダコ さんの書込 (2009/03/28(Sat) 18:56)

ファインマン物理学の 仮想仕事の原理の問題です．

• http://imepita.jp/20090327/501650

図のようなトラスで，対角線の支柱はみな5の長さ，水平の支柱はみな6の長さである． つなぎめは蝶番でみな自由に動く．トラスの重さは無視できる． a)図のように荷をかけたとき，支柱のどれとどれは，針金で代用できるか． b)支柱BD,DEの内部にはたらく力を求めよ．

aはなんとなく感覚でわかったのですがbがわかりません． 僕は以下のように考えましたがどこがおかしいか教えてください． BDが2Δxだけ縮むと点Cが(3/4)Δxだけ下がり，おもりは(3/8)Δxだけ下がるのでBD=(3/16)W DEがΔxだけ伸びるとおもりは(4/5)Δxだけ下がるのでDE=(4/5)W

ちなみに答えは a)AC,CE,EG,EF,ED,BC b)BD=(4/5)W,DE=(5/12)W です

mNeji さんのレス (2009/03/29(Sun) 02:31)

ペンダコさん，意外と難しい問題みたいですね．

まだ完全に理解していませんが，部分的にコメントさせて戴きます．

隣接する３頂点を結ぶ三角形で，少なくとも一辺は剛(圧力)で，他の辺は針金(張力)と思えます．例外はBDが剛であることですか．

各頂点が自由回転の自由度を持つ事から，各頂点ごとの力のバランスを考えればいいのでしょうか．

E点での垂直方向の力を考えます．ED,EFの間の張力をT， <pre> 2*(T*4/5) = W T = (5/8)W---(1) </pre>

F点での力のバランスを考えます．DF間の圧力をP，FG間の圧力をQとします．

F点での垂直方向の力について； <pre> T*4/5 - Q*4/5 = 0 Q = T = (5/8)W ---(2) </pre>

F点での水平方向の力について； <pre> P - T*3/5 - Q*3/5 =0 P = (T+Q)*3/5 = T*6/5 = (3/4)W ---(3) </pre>

mNeji さんのレス (2009/03/29(Sun) 17:51)

自己コメントです．

書いてから，考えていたのですが，先に書いたのは余りにも不確実なので撤回します．恐ら全ての点に関する力のバランスを連立して解かないと駄目なように思います．残念な事に，時間がすぐに取れないので，お急ぎでしたら他の方々にご教授いただかれて下さい．

Yokkun さんのレス (2009/03/29(Sun) 18:31)

ペンダコさん，こんにちは． 私もその昔考えた記憶があって，なつかしくなりテキストをあらためて見てみたら，赤鉛筆でチェックがあり，やはり，ん十年前にも解けなかったのだなあと思いました．

あらためて挑戦したところ， BDは1/2・W，DEは5/12・Wになりました．mNejiさんと同じように力のつりあいでも計算しましたが，やはりBDは1/2・Wになりました．ダメ押しで物理シミュレーションソフト『Phun』でおおざっぱなシミュレーションをしてみたら，どうも私の結果を支持しているように思えました．私のひとまずの結論としては，ファインマンのテキストの解答は間違えていて，BDは1/2・Wの抗力になるということです．DEは5/12・Wの張力で合っていますね．

仮想仕事の原理を用いるときには，私は逆にBDを伸ばして考えたのですが結果的に同じなので，ペンダコさんの考察に合わせますと，

BDを縮めると，C点が下がります． そこで，CGの水平から下がった角度を?θとおくと，点Eの下がりはh=6?θ． 同時にDからCEにおろした垂線が?θ傾くので，これによるBDの縮みは4?θです．

一方，ACが水平から下がる角度は2?θとなります． 同時にBからACにおろした垂線が2?θ傾くので，これによるBDの縮みは8?θ． 合計でBDは12?θ縮みます．仮想仕事の原理により，求める抗力をFとすると

F×12?θ＝W×6?θ

となり，F=1/2・Wを得ます． 同様にDEについて5/12・Wを得るのですが，ひとまずお返ししましょう．

mNeji さんのレス (2009/03/30(Mon) 03:02)

定性的な話で恐縮ですが，この構造を支えているのは，上側の柱; AB, BD, DF, FG であって，残りは上記の柱部分から針金で荷重に向かって引っ張られるだけのような気がします．

Yokkun さんのレス (2009/03/30(Mon) 08:58)

mNejiさん，CDも抗力になります．

各連結点でのつりあいで計算してみましたが（mNejiさんがやりかけたように） 以下，連結点AおよびBが支柱ABから受ける張力を 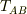のように表せば，

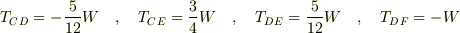
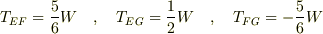
となります．負になったものは抗力になるわけです．

これらの計算は，たとえば連結点Aにおいて

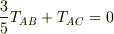
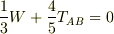
といった具合に連立させて，順次求めていきます（もう少しエレガントな解法もあるようですが）． 全体の力のモーメントのつりあいから，両端A，Bが支持台から受ける垂直抗力をそれぞれ1/3・W，2/3・Wと求めておくとラクですね．

結果，(a)の答えは張力が正であるAC,BC,CE,DE,EF,EGとなるのです． (b)は，この結果から明らかですが，これは違反．仮想仕事の原理を使わなければいけません．

mNeji さんのレス (2009/03/30(Mon) 23:12)

Yokkunさん，解説，有り難うございます．

＞mNejiさん，CDも抗力になります．

なるほどそうですね．先ず点Aの力の平衡をだしてから，点B.C,Dの縦方向には外力が働いていない事から，斜め成分の力は，張力と圧力が対になるようですね．同様に，点Gの力の平衡を出して，点Fの斜め成分にも同様な対条件が必要となりますね．

点Gは，回転の自由度だけて，位置の束縛があるので，水平方向の抗力が外力として入るとばかり思っていましたが，そんな外力はないようですね．(例えば，点Fからみたトルクの平衡)

＞(b)は，この結果から明らかですが，これは違反．仮想仕事の原理を使わなければいけません．

この場合の「仮想仕事の原理」というのはイメージし難いですね．BD間に働いている力だけを変化させてした仕事が，負荷Wの重力エネルギの変化に相当すると言う事みたいですね．この場合，他の要素は角度を変えても，エネルギ変化を生まないのでしょうか？

Yokkun さんのレス (2009/03/30(Mon) 23:46)

mNejiさん，こんばんは．

>BD間に働いている力だけを変化させてした仕事が，負荷Wの重力エネルギの変化に相当すると言う事みたいですね．この場合，他の要素は角度を変えても，エネルギ変化を生まないのでしょうか？

力を変化させるのでなしに，BDの長さだけ変えてBDが連結BおよびDに及ぼしている力に仮想仕事をさせたときに，その仕事による位置エネルギーの変化から力の大きさを得ようというわけですね．この場合，要素の質量を無視していますから，仮想仕事によるエネルギー変化は，荷重Wの上下分だけになります．

＃解説ページURL削除しました．

ペンダコ さんのレス (2009/03/31(Tue) 00:27)

遅くなりましたが，理解できました． 解説ページまで作って頂き，とても助かります． 詳しい解説ありがとうございました！

mNeji さんのレス (2009/03/31(Tue) 11:49)

＞仮想仕事によるエネルギー変化は，荷重Wの上下分だけになります．

これを拝見して，ある一つの部分の長さを仮想的に伸ばすとすると，

・圧縮部分で伸ばしが発生すると，錘が下がり， ・引張り部分で伸ばしが発生すると，錘が上がる．

と漫然に考えたのですが，その様な感じでもありません．どう考えればいいのでしょうか？

Yokkun さんのレス (2009/03/31(Tue) 19:36)

>・圧縮部分で伸ばしが発生すると，錘が下がり， >・引張り部分で伸ばしが発生すると，錘が上がる．

逆ですね．つりあい状態にある系に対して微小な変位を仮想するとき，その変位によって系にされた仕事は，変位の結果増加した系のエネルギーに等しいということ． もっとさかのぼった表現を使えば，機械における「仕事の原理」すなわち 「機械に対して入力された仕事と出力された仕事が等しい」 ということになります．

ですから，ある微小変位の結果エネルギーが増えたら，その変位のむきに力の成分があると判断できるわけです．仮想仕事の原理によって力を求める操作は，微小な変位に限られるので，変形の際に生じた2次の微小量は捨ててよいわけです．系を大きく変形させてしまうと，つりあい状態も変わりますから当然ですね．

上で力のつりあいによって張力が求められましたが，逆にその正負によってその部分を微小変形させたときに荷重部分がどれだけ上下するかを判断することができます．たとえば，CEをxだけ縮めると，その縮みの3/4だけEが上昇するといったぐあいです．

mNeji さんのレス (2009/03/31(Tue) 22:38)

＞もっとさかのぼった表現を使えば，機械における「仕事の原理」すなわち ＞「機械に対して入力された仕事と出力された仕事が等しい」

一般的に，「静止平衡にある系のエネルギ保存」が成立する，ということですね．

今の場合，左右の端点の拘束付きの静止平衡です．この拘束条件は，微小変位を何処かの部材に入れた変位から荷重Wの高さの変位を出す際に，取り込まれているとおもいます．

とすれば，微小変位を与えた部材への「機械に対して入力された仕事」は，微小変化を加えた部位が，圧縮性か張力性かによって，符号が自動的に決まるだろうと考えました．

ところが，左右の端点の拘束を考慮して，幾何学的な動きを見ると，荷重Wの高さの変位は下がる事はあっても，上がる事が無いようです．そこで混乱をしています．

一度オリジナルの本を拝見してから，考え直そうかと思います．

Yokkun さんのレス (2009/03/31(Tue) 23:15)

mNejiさん．左端は固定されていないことはご存知ですよね？ 伸び縮みさせる部材をばねに置き換えて考えてみてください．

• http://www.youtube.com/watch?v=3h_nxY8cIas

＃動画だけ貼りました．

mNeji さんのレス (2009/03/31(Tue) 23:31)

＞左端は固定されていないことはご存知ですよね？

ありゃ，左端は水平面に車輪で乗っている，言い換えれば，水平面上に束縛されているかと思っていましたが．床から離れると，左端に外力が掛からなくなるので，左端は常に床上にあるとしていました．

【追伸】

動画を拝見しました．とても説得力があります．こんなイメージを考えていたのですが，幾何学に弱い為に，間違っていた様です．お手数，有り難うございました．

この動画は，一時的なものにするには惜しい気もします．

mNeji さんのレス (2009/04/01(Wed) 01:08)

＞＃動画だけ貼りました．

有り難うございました．

『Phun』というのは，初めて拝見しました．興味深いものですね．時間ができたらトライしたいです．