すみません；；解き方が分からないので教えてもらえませんか？

娵さんの書込 (2009/03/23(Mon) 03:50)

x=2+√3，y=2-√3のとき，xy=(ア) このアに入る答えが分かりません；；どなたか教えていただけませんか？

, のときの値はいくらになりますか?

え〜っと xy＝（a＋b）×（a−b）でいいのでしょうか？あと√の計算方法がちょっと分からないのですが教えていただけませんか？

すみません〜え〜っとxy＝４−√９までは出せたんですがここからさらに答えは出るのでしょうか？

$\sqrt{x}$ とは2乗(2回かけ算)してになるような非負の実数です．例えば，

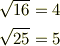
$\sqrt{16}&=4\\\sqrt{25}&=5$

等です．

定義により

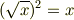
$(\sqrt{x})^2&=x$

も成り立つ事は分かりますね．

なるほどですと４−√９は４−３＝１になるんですね！ありがとうございます＾＾；たすかりました；；

もうご質問は終わったとおもいますが，途中の式に付いてtoorisugari no Hiroさんがお書きになった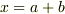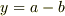，＞ x=a+b , y=a-b のとき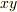の値はいくらになりますか?

について，関連の意見を書きます．ご自分でも＞え〜っと＞xy＝（a＋b）×（a−b）でいいのでしょうか？

と書かれていますが，この先について，分配の法則，積の順番の交換などから

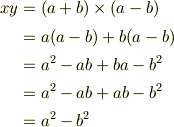
$xy &= (a+b) \times (a-b)\\&= a(a-b) + b(a-b)\\&= a^2 -ab + ba - b^2 \\&= a^2 -ab + ab - b^2 \\&= a^2 - b^2$

これを，四角形の面積に付いて考えます．

<pre>

一辺の長さａの正方形ＯＰＱＲ，一辺の長さbの正方形ＳＴＱＷとＴＵＶＱとを考える．

ＲＷＱＶ ┌────────────┬───┬───┐ ││││ ││││ ││││ Ｙ┼───└───┼───┘ │Ｓ│ＴＵ ││ ││ ││ ││ ││ ││ ││ │││ │││ │││ │││ └────────────────┴───┼ ＯＰＸ

線分ＶＵの延長線と線分ＯＰの延長線との交点をＸ，線分ＴＳの延長線と線分ＯＲとの交点をＹとする．

こうすると，定義から明らかに，

・線分ＯＸの長さ＝ａ＋ｂ≡ｘ・線分ＯＹの長さ＝ａ−ｂ≡ｙ

となるので，求めるべきxyは「長方形ＯＸＵＹの面積」になります．

このうち，長方形ＰＸＵＴと長方形ＹＳＷＲとは合同だから，それらの面積は等しい事から，

長方形ＯＸＵＹの面積＝長方形ＯＰＴＹの面積＋長方形ＰＸＵＴの面積＝長方形ＯＰＴＹの面積＋長方形ＹＳＷＲの面積＝多角形ＯＰＴＳＷＲＯの面積＝正方形ＯＰＱＲの面積−正方形ＳＴＱＷの面積故にｘ＊ｙ＝ａ＊ａ−ｂ＊ｂ </pre>

なんと細かい解説ありがとうございます；；なんとか答えを出すことができました，ありがとうございました＾＾