lie微分の定義
lie微分の定義
ファイル さんの書込 (2009/03/12(Thu) 18:24)
関数のLie微分について,質問があります. Lie微分とは,おおまかに言えば,ある点のスカラー関数やベクトル場を,曲線のパラメータλについて不変な移動「Lie移動」によって,別の点に移し,そこでのスカラー関数やベクトル場と差を取り,λで割って極限を取る.というようなことであると理解しています. まだ勉強したてなので,数学的にあやふやな点があることをお許しください.
ところで,関数のLie微分の場合, 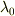 において,
において, 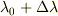 での
での  と同じ値を持つような新しい関数
と同じ値を持つような新しい関数 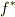 を定義して(私は,このことはLie移動とは関係ないと考えています.)
を定義して(私は,このことはLie移動とは関係ないと考えています.)
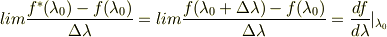
手持ちの教科書では,ここで「Lie移動により,新しいスカラー場 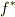 が,
が, 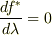 を満たすように定義される.従って,
を満たすように定義される.従って, 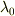 での
での 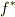 の値は,
の値は, 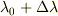 での
での 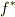 の値と同じである.」
と記述されているのですが,この
の値と同じである.」
と記述されているのですが,この 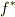 に関するLie移動の記述は,
上記のLie微分の定義に全く組み込まれていないように思います.
つまり,上記の定義は,普通の微分となんら変わらないように思うのですが,どうなのでしょうか?
(スカラーの共変微分は偏微分に等しいのと似たようなことなのだろうか?などと予想していますが・・・.)
に関するLie移動の記述は,
上記のLie微分の定義に全く組み込まれていないように思います.
つまり,上記の定義は,普通の微分となんら変わらないように思うのですが,どうなのでしょうか?
(スカラーの共変微分は偏微分に等しいのと似たようなことなのだろうか?などと予想していますが・・・.)
宜しくお願いします.
Re: lie微分の定義
toorisugari no Hiro さんのレス (2009/03/12(Thu) 18:35)
> 「Lie移動により,新しいスカラー場 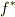 が,
が, 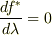 を満たすように定義される.従って,
を満たすように定義される.従って, 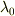 での
での 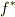 の値は,
の値は, 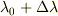 での
での 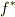 の値と同じである.」
の値と同じである.」
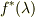 は
は
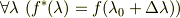
という「曲線上で一定値をとる」(=Lie移動で変わらない=「Lie移動された」)関数として定義されているということでは?
> 上記の定義は,普通の微分となんら変わらないように思うのですが,どうなのでしょうか?
スカラーに関しては方向微分,つまり,偏微分の一般化と考えて良いと思います. (ただ,普通の偏微分は「他の座標を変えない経路上での微分」に対して,Lie微分は「与えられた(流れから作られる積分)曲線上での微分」という違いはありますが...)
Re: lie微分の定義
ファイル さんのレス (2009/03/12(Thu) 22:08)
なるほど.
しかし,微分を考える際,「特定の」2点のみを考えれば良いわけですよね?
例えば, 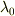 と
と 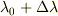 によって指定される曲面上の2点を考える場合,その2点のあいだに
によって指定される曲面上の2点を考える場合,その2点のあいだに 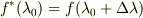 という関係の関数だけを定義すれば,他の
という関係の関数だけを定義すれば,他の  での関数
での関数 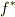 の値はどうでもよくて,つまり,「曲線上で一定値をとる」のような要請は必要ないような気がするのですが.
の値はどうでもよくて,つまり,「曲線上で一定値をとる」のような要請は必要ないような気がするのですが.
Re: lie微分の定義
toorisugari no Hiro さんのレス (2009/03/13(Fri) 11:31)
Lie微分をどのように捉えるかに過ぎないでしょうね.
> 「特定の」2点のみを考えれば良いわけですよね?
とかんがえてももちろんかまいません.
流れが与えられている系で物理量の時間変化を考えます.変化には流れによる変形に起因する分とそれ以外の理由で変化する分があります.後者を取り出す操作がLie微分だと思います.
Lie移動された量をLie微分しても0です.これは「保存された場(=定常な場)」に当たります.Lie微分は「保存された場=Lie移動された量」からどれだけずれているかを示す量だと思います. # ここら辺は私個人の感覚であって,正確な記述ではありません.
もちろん2点のみで考えていいのですが,流れ全体を見通す視野があってもよいと思います.
Re: lie微分の定義
ファイル さんのレス (2009/03/13(Fri) 15:00)
ありがとうございます.
「特定の2点間」という考え方だと,特にLie移動の概念は必要ないように思います.つまり,普通のパラメータ微分と同じような意味になると思います.
一方,toorisugari no Hiroさんのおっしゃるように,Lie移動された(流れで変わらない)新しい関数 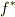 と,元の関数
と,元の関数  の差を取る(ということですよね?)と,流れ以外の理由での変化分を求める微分,ということになりますね.
の差を取る(ということですよね?)と,流れ以外の理由での変化分を求める微分,ということになりますね.
そのように考えると, 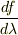 という同じ式に対して,通常のパラメータ微分という捉え方と,Lie微分という捉え方の,二通りの解釈が出来てしまいますが,それでも良いのでしょうか?
という同じ式に対して,通常のパラメータ微分という捉え方と,Lie微分という捉え方の,二通りの解釈が出来てしまいますが,それでも良いのでしょうか?
Re: lie微分の定義
toorisugari no Hiro さんのレス (2009/03/13(Fri) 15:11)
> そのように考えると, 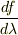 という同じ式に対して,通常のパラメータ微分という捉え方と,Lie微分という捉え方の,二通りの解釈が出来てしまいますが,それでも良いのでしょうか?
という同じ式に対して,通常のパラメータ微分という捉え方と,Lie微分という捉え方の,二通りの解釈が出来てしまいますが,それでも良いのでしょうか?
この式 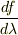 が何を意味しているのかは文脈によって変わるので,解釈に何通りかあってもおかしくないと思います.
# 中身は変わらないように新しい考え方を導入したということですね.
が何を意味しているのかは文脈によって変わるので,解釈に何通りかあってもおかしくないと思います.
# 中身は変わらないように新しい考え方を導入したということですね.
Lie微分が普通の微分と違うのは,ベクトルに対する微分です.そのときLie移動という考え方が生きてくると思います. # 平行移動(接続)を使わずに2点間のベクトルをどう比較すればいいのでしょう? # ベクトルに対するLie微分からテンソルやn形式のLie微分も定義されます.
> Lie移動された(流れで変わらない)新しい関数 |04f5f57d53e9bffe95e1969a780328c1|
「流れで変わらない」というより「流されただけの」のほうが私はしっくりします.
Re: lie微分の定義
ファイル さんのレス (2009/03/13(Fri) 16:39)
確かに,ベクトルのLie微分はLie括弧になるので,普通の微分とは全く違いますね.今回はスカラー関数だったので,あまり違いが感じられなかったのですね. なんとなく納得しました. (一形式やテンソルのLie微分もすでに学びました.)
申し訳ないのですが,もう一つ疑問があります.
Lie微分の定義は,関数にしろベクトルにしろ,toorisugari no Hiroさんのお言葉を借りるならば,流されただけの関数(ベクトル)と元の関数(ベクトル)を比べる,ということになります.
疑問というのは,その流されただけの関数はいつでも存在するのか?ということです.その新しい関数は,ベクトル場に沿って不変でなければなりません.
つまり,Lie微分がゼロになるような関数でなければならないはずです.そのように考えると,新しい関数 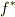 というのは,
・
というのは,
・ 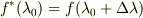 という値を持たなければならない.
・流れに沿って,
という値を持たなければならない.
・流れに沿って, 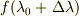 を保存しなければならない.
という二つの制約が課されますが,いつでもそのような都合の良い関数を取ることが出来るだろうか?と思いまして・・・.
を保存しなければならない.
という二つの制約が課されますが,いつでもそのような都合の良い関数を取ることが出来るだろうか?と思いまして・・・.
Re: lie微分の定義
toorisugari no Hiro さんのレス (2009/03/13(Fri) 17:53)
> 疑問というのは,その流されただけの関数はいつでも存在するのか?ということです.
ある流線(積分曲線) 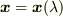 上でスカラー関数
上でスカラー関数 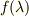 がすでに存在しているという前提のもとで,その流線上で一定値を取るスカラー関数
がすでに存在しているという前提のもとで,その流線上で一定値を取るスカラー関数 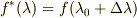 を作るという考えのどこに疑問をもたれているのかちょっと分かりません.
# もちろん,その流線以外での
を作るという考えのどこに疑問をもたれているのかちょっと分かりません.
# もちろん,その流線以外での 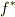 は未定義です.
# 当然,
は未定義です.
# 当然, 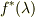 は
は 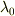 ,
, 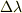 が変われば取り直します.
が変われば取り直します.