digi さんの書込 (2009/03/06(Fri) 02:05)

結晶中を電子が運動するときの移動度について調べています． ふつうは，移動度は 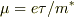と表されると思います． 知識が少ないため，厳密な導出方法がわかりませんが，本を読んでいるとちょっと簡単な導出方法が書いてありました（たぶん厳密ではないと思いますが）．でも，いくつかわからない点がありまして，質問させてもらいました．

結晶中の電子が移動するとき，原子に衝突するために運動が妨げられます．1個の電子の散乱緩和時間を とすると，運動方程式は 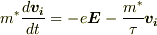・・・(1)

≪まず，1つ目の質問ですが，上式の右辺第2項は衝突項だと思うのですが，どうしてこのような形で運動方程式に入ってくるのかがわかりません．≫

つぎに，すべての電子がn個として，(1)の和をとります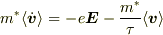． ・・・(2)

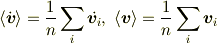
定常的な系では，すべての平均量の時間変化はゼロであるから(2)の左辺はゼロとなる．

≪ここで2つめの質問です．「定常的な系では，すべての平均量の時間変化はゼロである」とはどういうことでしょうか？≫ ≪3つ目ですが， はそのままでもいいのでしょうか？≫

このあとは速度と電界の比が移動度になるということです．これは移動度の定義ですね．

わかる範囲でいいので，お願いします．

toorisugari no Hiro さんのレス (2009/03/06(Fri) 11:38)

> ≪まず，1つ目の質問ですが，上式の右辺第2項は衝突項だと思うのですが，どうしてこのような形で運動方程式に入ってくるのかがわかりません．≫

たくさんの結晶粒子との相互作用で「統計的」に粒子は減速します．それを表したものです．

> ≪ここで2つめの質問です．「定常的な系では，すべての平均量の時間変化はゼロである」とはどういうことでしょうか？≫

「定常的」とはどういうことですか?

> ≪3つ目ですが， |a6f317b268ae825d94f832f970af607c| はそのままでもいいのでしょうか？≫

よく考えると難しい問題ですが，(1)式の段階で はパラメータと考えて良いからです．

ASA さんのレス (2009/03/06(Fri) 21:12)

はじめまして，digiさん．

単純な力学モデルをベースに考えると理解しやすいと思います．

1つ目の質問： 電気抵抗を空気抵抗を置き換えることで，雨粒の落下速度を求める（最終速度）問題と比較できます． 抵抗項として，よく知られているのが速度vに比例する項とv^2に比例する項です．速度がたいして大きくないときは，v^2比例項は無視できるとした近似式が，示された式(1)だと思われます．

2つ目の質問： 「定常的な系」：難しい言葉を使っていますが，ほぼ最終速度に達した状態のみを考察対象にするという意味合いですね．

3つ目の質問： ミクロ的に考えると難しいですね．移動度がマクロ的量なので，緩和時間を平均で考えることが正当化されると考えられます．例えるなら，降雨量を考えるとき，個々の雨粒の大きさや最終速度を気にしないようなものですね．

digi さんのレス (2009/03/06(Fri) 23:30)

3つ目の質問は大丈夫です．わかりました．

1つ目ですが，衝突項は，質量に散乱確率をかけて速度をかけて-1倍して力になっているということですよね．この感じがつかめません．

2つ目ですが，定常的な系を速度が最終状態に達していると考えたとき，速度の時間変化の総和は0というのは，どういうことでしょうか？加速度の総和が0．電子がいろんな方向に散乱されているからでしょうか？

ASA さんのレス (2009/03/07(Sat) 09:26)

>1つ目 速度に比例する抵抗力は，イメージしやすいと思います． 定間隔で格子があるとし，１つの格子からある一定の散乱力を受けるとすれば， 単位時間に当りに受ける散乱力は，電子の速度に比例します． (速いほど，たくさんの格子とぶつかり，より多くの抵抗を受ける) そしてこの一定の散乱力が，緩和時間の逆数に比例しているということですね． (散乱力が強いほど，短時間で緩和する) 確かに，「統計的」という説明では，物理的意味は通じないでしょう．

>2つ目 「定常的」とか，「最終状態」ということに違和感があります． ほぼ最終速度で運動している電子が存在する状況とは，明確に区別した方がよろしいでしょう． 結晶に外部から電場をかければ，分極しておしまいです．内部電場は，外部電場と外部電場により誘起された分極電場がキャンセルし，力が働いてない状態になります．

ミュフ猫 さんのレス (2009/03/07(Sat) 10:35)

ASAさん，こんにちは．

>結晶に外部から電場をかければ，分極しておしまいです．内部電場は， >外部電場と外部電場により誘起された分極電場がキャンセルし，力が >働いてない状態になります．

誘電体は不導体ですよね？ 分極で内部電場が弱まることはあっても，０にはならないのでは？ たとえ，導体であっても，電極と直に接続され（つまり，回路導線が 存在しないような状態），キャリア電子の逃げ道がある状態（つまり， 通電状態）ならば，電荷の偏りが生じず，内部電場は外部電場に一致 しそうに思うのですが．

ASA さんのレス (2009/03/07(Sat) 11:50)

ミュフ猫さん

>誘電体は不導体ですよね？ はあ？移動度の話をしているのにわけがわかりません． 誘電体のようにローカライズした電子系で移動度がどのような意味を持つのか， 説明をお願いします．

>導体であっても，電極と直に接続され（つまり，回路導線が 存在しないような状態），キャリア電子の逃げ道がある状態（つまり， 通電状態）ならば，電荷の偏りが生じず，内部電場は外部電場に一致 しそうに思うのですが． いまいち，状況が想定しにくいです．具体例で説明をお願いします． 一般には，静的外部電場に対して導体の内部電場は０になるはずですが， 移動度(電気抵抗)の違いによって静電シールド効果が違う実例をご存知でしたら紹介してください．

ミュフ猫 さんのレス (2009/03/07(Sat) 12:14)

ASAさん

返信どうもです． 高校レベルで聞いてください．ｗ まず，「分極」と言う用語で単純に誘電体を連想しました． よって，内部電場が０になるということに疑問が生じました． 次に，導体ならば「静電誘導」を起こすので，誘電分極（電子分極， イオン分極など）は無関係では？と思いました． 導体内のキャリア電子の移動現象をモデル化する際，「加速→衝突→失速」 を周期τで繰り返す説明が，高校レベルでよく見受けられます． つまり，たとえ導体であっても「加速」は必ず発生するので，すなわち， 内部に電場が存在するということだと，浅〜く理解してます．

すみません．ちょっと，勘違いしてたかもしれません．

yama さんのレス (2009/03/07(Sat) 13:59)

横から失礼します．

結晶中の電子の移動度の問題なので，金属結晶または半導体結晶が想定されているのだと思います． その結晶が電池などに接続されていて，内部に電場が存在する状態が保たれていると考えるのでしょう．電子の流入と流出があるという点で，静的な外部電場の中に置かれている場合とは状況が違うように思います．

従って，この場合の定常的な状態は，定常電流が流れている状態でしょう． 厳密に定常電流でなくても，散乱緩和時間程度の間に電流がほとんど変化しなければ近似的に定常と見なせるでしょう．

toorisugari no Hiro さんのレス (2009/03/07(Sat) 19:44)

ASAさんのご説明で明快にわかると思いますが，

> 速度に比例する抵抗力は，イメージしやすいと思います．
>定間隔で格子があるとし，１つの格子からある一定の散乱力を受けるとすれば，
>単位時間に当りに受ける散乱力は，電子の速度に比例します．
>(速いほど，たくさんの格子とぶつかり，より多くの抵抗を受ける)

電子の速度に比例するのは力あるいは単位時間あたりの運動量変化であって，単位時間あたりの力ではないですね．(ま，typoなのでしょう．)

あと気になったのは，散乱をどう考えるかの問題です．

電子が格子結晶に散乱するとき，一回の散乱ではいろいろな方向に散乱しうるので，一回の運動量変化はばらついていますが，平均的にみると速度に比例しているとみることができます．

「１つの格子からある一定の散乱力を受ける」という根拠がわからないので，説明していただけませんか?(散乱モデルの違いだとは思いますが．)

> そしてこの一定の散乱力が，緩和時間の逆数に比例しているということですね．

というより，力と速度の間の比例定数で緩和時間を定義すると考えるのが自然では?

toorisugari no Hiro さんのレス (2009/03/07(Sat) 20:03)

> 「定常的な系」：難しい言葉を使っていますが，ほぼ最終速度に達した状態のみを考察対象にするという意味合いですね．

この式 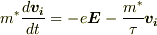をもとに考えるなら，そうでしょうね．でも，それでは平均操作が不要になります．

ここでは，この方程式を離れて，マクロな意味で「定常的な系」という言葉を使っていると思います．

一個一個の電子は加速減速を繰り返しながら，運動しているが，全体系は「平衡状態」なっている．そして，そのとき(，マクロな振動運動などがないと仮定すると) ，平均物理量は時間的に変化しない定数になり，系はマクロな意味で「定常」になっている． という解釈ではないですか?

# ま， を定数とみる以上，平均するより，素直に終状態で考えるのがわかりやすいし，自然ですが．

本当は 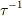を確率変数とみる方が，より良いと思います．そういう意味で，≪3つ目ですが， はそのままでもいいのでしょうか？≫というスレ主さんの疑問は的を得ています．

ASA さんのレス (2009/03/07(Sat) 21:09)

toorisugari no Hiroさん >ま，typoなのでしょう．) 確かにtypoですね．

>電子が格子結晶に散乱するとき，一回の散乱ではいろいろな方向に散乱しうるので，一回の運動量変化はばらついていますが，平均的にみると速度に比例しているとみることができます． そもそも，ミクロ的には，確率的にしか言及できない，つまり，ランダムな運動をしていますから，マクロ的な平均速度でしか意味がないような気がします． 個別電子の速度云々を初めに述べることが適切でないように思えます．

>「１つの格子からある一定の散乱力を受ける」という根拠がわからないので，説明していただけませんか? ＋チャージの格子点と，-チャージの伝導電子が相互作用し，ある一定の運動量（エネルギー）を交換するというモデルですね，格子振動のエネルギー準位は，量子化されているので，そこそこ妥当でしょう．

>比例定数で緩和時間を定義すると考えるのが自然では? ミクロな量子論的考えだと，?E・?t＝constなので，電子が失うエネルギーが大きいほど緩和時間は短くなることがいえますけど． マクロ視点で，一貫性を持たせる立場ならそのような方法もありえますね． しかし，ミクロ的な見識をある程度入れても悪くはないと考えます．

>それでは平均操作が不要になります． だから，その論法が気に入らないわけです．

>「定常的な系」という言葉を使っていると思います． >全体系は「平衡状態」なっている． 「平衡状態」なら，違和感は感じませんね． >>定常的な系では，すべての平均量の時間変化はゼロであるから(2)の左辺はゼロとなる． 上記の説明を噛み砕くとそのようなことになると思いますが，初学者向けとは思えません． そういった，疑問対して >「定常的」とはどういうことですか? と返すのは，感心しません．

>平均するより，素直に終状態で考えるのがわかりやすいし，自然ですが． やはり，そうですよね．

>確率変数とみる方が 量子論的な相互作用の強さとみる方が，物理的意味を明確にできるのでよりよい考えます(なんにせよ確率変数ですけど）．

ASA さんのレス (2009/03/07(Sat) 21:38)

yamaさん >定常電流が流れている状態でしょう． 移動度の定義をonly ケースしか成立しないものと狭く限定する必要はないと思います．ほぼ一定の平均電子速度が存在する系をも含めて広く定義できたほうが，物理量としての移動度の有効性が高まりますよ．

yama さんのレス (2009/03/08(Sun) 00:59)

確かにそうですね．

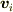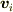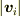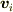ところでdigiさんの３つ目の質問ですが， を定数のように扱うことに疑問を感じておられるのではないでしょうか？ 電子の速度 が変化すると，単位時間当たりの平均衝突回数が変化するため散乱緩和時間も変化しそうに思えますね． その点については次のように説明できます． 電子は電場がなくてもランダムな熱運動をしています．もちろん平均の速度は0です． 電場が存在する場合は，平均の速度は0でなくなりますが，それが です． しかし，熱運動の速さは に比べて圧倒的に大きいので，単位時間当たりの衝突回数は実質的に熱運動の速さだけで決まり，緩和時間 は に無関係な定数と見なすことができるというわけです． ただし，熱運動の速さは温度によって変化するため は温度の関数となり，従って電子の移動度も温度によって変化します．これには温度による格子振動の変化も関係しますが・・・．

digi さんのレス (2009/03/08(Sun) 04:02)

いつのまにやらたくさんの返信をいただきまして，ありがとうございます．

いま考えているのは，yamaさんがおっしゃるとおり，半導体結晶です．

1つ目の質問については， 散乱力は電子の運動量の時間的変化に比例する． 散乱力が大きいと散乱緩和時間は短くなる． だから，衝突項は 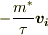となるってことでいいのでしょうか．マイナスは速度と力が逆向きということですが，必ず逆向きなのでしょうか？

時間的な流れを考えたとき，電場による力はつねに働いているのに，散乱力は散乱緩和時間間隔で働きますよね．そのような違いがあるのに散乱力を運動方程式にいれるということに違和感がありました．散乱確率をかけているからそれでいいような気もするのですが．

2つ目の質問ですが， 1個1個の電子はランダムに散乱されるが，全体的にみると電子の速度は一定に見えるということですね．つまり，|76cb99aea49a27b164b6c6f543486ea0|は成分が定数だと考えてもよく，その時間変化はゼロということですね．

3つ目の質問はyamaさんが返信をくださいましたが，電子の熱運動がよくわかりません．熱運動が|76cb99aea49a27b164b6c6f543486ea0|より圧倒的に大きいということは，電子は電場の影響をほとんど受けていないということでしょうか？

ASA さんのレス (2009/03/08(Sun) 07:27)

yamaさん 横からすいません． 話題となっているのは，非弾性散乱ですよね．外場なしで，熱平衡状態にあるなら，平均的には弾性散乱とみなせるので，話が違うような気がします．

digiさん 3つ目の質問は，いい質問ですが，あまり深く追求しない方がよいと考えます． >>よく考えると難しい問題ですが，(1)式の段階ではパラメータと考えて良いからです． これが無難な，回答だと思います．

ASA さんのレス (2009/03/08(Sun) 07:56)

digiさん追伸です． >時間的な流れを考えたとき，電場による力はつねに働いているのに，散乱力は散乱緩和時間間隔で働きますよね．そのような違いがあるのに散乱力を運動方程式にいれるということに違和感がありました． 確かにそうですよね．(1)自体が，平均化されたものに対して成立する式なのに，以降でさらに平均操作を持ち出す論法は，気に入りません． 電子のある時刻における位置はばらばらと考えられるので，空間平均ないしは，多数の平均を考えた場合に(1)が成立すると看做せるはずです．

>マイナスは速度と力が逆向きということですが，必ず逆向きなのでしょうか？ 電子から格子へエネルギーを渡す非弾性散乱過程の効果を取り入れているので−符合のみでよいはずです．(個別で見ると電子がエネルギーをもらう過程もありますが，熱平衡状態にあるなら平均的には弾性散乱とみなせます，つまり電子が格子間隔を渡る時間より早く格子間での熱的緩和が行われることを仮定しているわけです．）

yama さんのレス (2009/03/08(Sun) 09:08)

電場がなければ熱平衡状態ですが，電場があって電流が流れている場合は熱平衡状態ではありません．． 結晶を静的な外場の中に置くと，静電誘導や分極によって初めと異なる平衡状態に移行しますが，電池につないだ場合は電子の流入と流出が続くため熱平衡状態に達することはありません．

>熱運動が|76cb99aea49a27b164b6c6f543486ea0|より圧倒的に大きいということは，電子は電場の影響をほとんど受けていないということでしょうか？

平均速度に対する影響と，平均の速さ(速度の絶対値)に対する影響には違いがあります． 平均速度は，0から 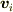に変わるので電場の影響は大きいのですが，平均の速さはほとんど変化しないので平均の速さに対する電場の影響は無視できます．

ASA さんのレス (2009/03/08(Sun) 12:22)

yamaさん 「熱平衡状態」の定義が違いますね． 比熱なんかでは，格子振動が大きな比重を占めます．ここでは，各格子点への等エネルギー分配が成立している状態をとりあえず「熱平衡状態」と述べています． 導体に均一な定常電流を流したばあい，導体の全ての部分が等しい温度になることがありますが，こういう等温状態にあるにもかかわらず「熱平衡状態」にないと定義するのは，ちょっと考えずらいですね(そもそもキャリア単体の温度なんて測定しようがないような気がしますが)．

＞平均の速さはほとんど変化しないので平均の速さに対する電場の影響は無視できます． 具体性に欠けるので，ある温度Tでの平均自由行程lの値を持ち出すとかしたほうが説得力が増すと思います(絶対0度付近なら，平均の速さなんてたいした値でない気がしますけど)．

yama さんのレス (2009/03/08(Sun) 13:45)

導体に定常電流が流れている場合は，ジュール熱が発生しますが，その熱は熱放射として導体表面から外部に出て行きます． この場合導体の内部と表面付近には温度差が生じていて，内部から表面に向かう熱の流れがあります． このような状態は，定常状態ではあっても，熱平衡状態ではありません． キャリア単体の温度が測定しようがないのは，平衡状態であってもなくても同じだと思います．

>具体性に欠けるので，ある温度Tでの平均自由行程lの値を持ち出すとかしたほうが説得力が増すと思います

平均自由行程が速さにほとんど関係しないことは重要ですが，緩和時間は平均自由行程だけでなく平均の速さにも関係するので，緩和時間が一定になるためには平均の速さがほとんど変わらないことが必要になってきます． 温度が変化すると緩和時間も変化しますが，それは平均自由行程が温度によって変化するためではなく，平均の速さが温度によって変化するためです．

絶対0度付近については，別の議論が必要でしょうね．

ASA さんのレス (2009/03/08(Sun) 15:22)

>その熱は熱放射として導体表面から外部に出て行きます． これには異論がありますね．熱放射のみを考えるなら，内部から直接電磁波として放出されるものがあるでしょう．完全黒体を想定しているわけでないし，また，進入長より，極めて細い半径の導線だったらどうなのとか． なんにせよ，表面でのみしか準位間遷移がありえないとする物理的理由はないと思います（決して温度差があるから熱輻射するわけではない）．導線各部で同様な準位間遷移をするなら，当然輻射バランスがとれるので，各部の温度は同じになるはずです．（輻射バランスが崩れるのは，外部との境界のみですね） 質点の熱振動による導体各部へのエネルギー輸送と電磁波による外部へのエネルギー輸送をごっちゃにしているように思えます． 具体的事例で考えると，白熱電球のフィラメントなどは，内部の方が温度が高いので液体状になって表面だけが固体状態になりえるいうわけですね(有り得ない)．

＞キャリア単体の温度が測定しようがないのは，平衡状態であってもなくても同じだと思います． キャリアから格子への衝突によるエネルギー輸送があるので，熱平衡ではありえないという考えかと推察したものでそのようなコメントを致しました．温度というマクロ量に関して，空間的にオーバーラップしているキャリアと格子とを切り分けて考えるのが物理的に無意味だということに同意してもらえるならこの話は終わりです．

＞平均自由行程が速さにほとんど関係しないことは重要ですが， 引用部以下は，意味不明なので解説をよろしくお願いします．どのようなモデルを想定して，どのように定義しているのか明確にして欲しいです．

yama さんのレス (2009/03/08(Sun) 17:36)

もちろん内部でも電磁波の放出は起こっていますね． しかし，放出された電磁波は導体を透過して直接外に出るのではなく，外に出るまでには吸収と放出が繰り返されると思います． ただし侵入長より極めて細い細線の場合は，直接外に出て行く割合が多いでしょうね． いずれにしても導体内部から表面へそして外部へと向かうエネルギーの流れがあるわけです． 一般に系の内部に巨視的なエネルギーの流れがある場合は，それが熱伝導によるものであろうとなかろうと，熱平衡状態とは言えないと思います．

平均自由行程についての議論はあまり厳密なものではありません． 厳密には散乱断面積を考えるべきでしょうが，簡略化して剛体球との衝突のようなものを考えたわけです． この場合の平均自由行程は，衝突してから次の衝突までの平均の移動距離なので，速さにはほとんど関係しないと思います．しかし速さが大きくなれば衝突から次の衝突までの平均の時間は短くなるでしょう．

追記 剛体球との衝突と見なすのはあまり適切ではないようです．電気抵抗の温度依存性が正しく導けません． より正確には量子論的な取り扱いが必要であって，その場合は平均自由行程が温度に関係するようです．

nomercy さんのレス (2009/03/08(Sun) 18:57)

横から失礼します．

digi さんの質問の繰り返しにもなりますが，

>しかし，熱運動の速さはに比べて圧倒的に大きいので，単位時間当たりの衝突回数は実質的に熱運動の速さだけで決まり，緩和時間はに無関係な定数と見なすことができるというわけです．

これが良く分かりません． ここで言っている「熱運動の速さ」とは何のことですか？ また，緩和時間は

τ = a v_T + b v_i (v_T: 熱運動の速さ)

の形に表されるということですか？

yama さんのレス (2009/03/08(Sun) 21:15)

熱運動の速さというのは，文字通り熱運動している電子の速さであって，常温では10km/s程度になります． それに対して，導体内部で電場の方向に移動する平均の速さは，多くの場合1mm/s以下です．

緩和時間は衝突から次の衝突までの平均の時間であって，平均自由行程を平均の速さで割ったものです．

nomercy さんのレス (2009/03/08(Sun) 22:04)

√(2T/m*) を熱運動の速さと呼んでるわけですか？ 一応確認しておきたいのですが，電場下での平均の速さはどう決めてるんですか？

それで何故，緩和時間は v_i に依存しないのですか？

nomercy さんのレス (2009/03/08(Sun) 22:17)

自己レス

線形応答理論を思い起こすと， 電場が零のときの揺らぎの大きさで伝導率が決まるわけだから， 緩和時間は

τ = (電場に関係ない，熱運動の速さだけで決まる項)＋（電場を含む項）

となるのかな． そして，第二項は電場が小さいときは当然無視できる，と．

yama さんのレス (2009/03/08(Sun) 22:28)

熱運動の平均の速さはrmsでは 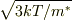，速度の絶対値の平均では 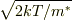になります． 緩和時間の計算には，後者を用いるほうがいいでしょうね．

電場方向に移動する平均の速さは電流密度を電荷密度で割って求められます． 電荷密度は自由電子の（個数）密度に電子の電荷を掛けたものです．

ASA さんのレス (2009/03/09(Mon) 08:21)

>熱運動の平均の速さは ああ，やはりそういうこと(前に絶対0度をだした理由)． 比熱の話を出しましたが，特性温度以上なら，格子比熱の古典モデルで説明できて，キャリアの比熱なんて無視できますね． キャリアに対して等エネルギー分配が成立しないとみえるから，熱運動での平均の速さというものは説得力を持たないのですよ． 金属の電子理論なら，フェルミ面とかをもちださないと，うまくないような気がします．

元の移動度の話に戻すと，キッテルでは，ｋ空間フェルミ球に対する運動方程式F=h~(dk/dt)から，衝突時間τに対して，フェルミ球ズレは運動方程式を0からτまで積分することにより得られ，速度増分(ドリフト速度)v=-eEτ/mとなる． ここから電場に対するドリフト速度の大きさの比として移動度を定義するとμ=v/(-E)=eτ/m．こうした理解のほうが変なことに悩まなくてすむからいいような気がしますね．

ちなみに平均自由行程lは，l=vf*τ;vf:フェルミ面での速度(これは温度でほとんど変らない) Cuでl(300K)=3*10^(-6),l(4K)=0.3;(cm)とあり，明らかに温度依存します．

ASA さんのレス (2009/03/09(Mon) 08:36)

>一般に系の内部に巨視的なエネルギーの流れがある場合は，それが熱伝導によるものであろうとなかろうと，熱平衡状態とは言えないと思います． 思い込むのは，ご自由ですけど． 別に，断熱状態でも，投入ワット数に対して，比熱が十分大きいなら，温度上昇は極めて緩やかになるから，ほぼ温度一定状態と看做せるので全く問題ありません．ましてや，格子間緩和時間が極めて短いとする仮定により，温度の均一性は保たれますし(熱伝導率∞)．

yama さんのレス (2009/03/09(Mon) 15:17)

電子が原子に衝突するという簡単なモデルによって結晶中の電子の移動度がどのように導かれるかということが問題になっているわけであって，量子力学的に厳密な導き方を問題にしているわけではないと思います． もちろんこの古典的なモデルでは実験結果に合わない点があるため最終的には量子論的な考察が必要になります． しかし古典論の範囲でも部分的には実験結果に合う結果を導くことができます． 古典論でどこまで説明でき，どこに限界があるかを検討することは意味のあることだと思います． そして，古典論の枠内でのモデルとして電子の熱運動を考えるモデルがあり，歴史的に見ても量子論的なモデルに先行してこのモデルが提唱されているわけです． しかし，電気抵抗の温度依存性が正しく導けないところにこのモデルの限界があり，量子論的考察が必要になります．しかし，それは次の段階の話であって，まず古典論の枠内で説明を考えることが本スレの趣旨に合っているように思います．

ところで，どうして比熱の話が出てくるのかよく分かりません． 確かに半導体ではキャリア自体の数が少ないため，キャリアの比熱は無視できると思いますが，そのことが電子の移動度にどう関係するのでしょうか？

熱平衡の定義についても疑問点はありますが，よく分からない点もあるので，これについては保留としておきます．

toorisugari no Hiro さんのレス (2009/03/09(Mon) 16:44)

> この古典的なモデルでは実験結果に合わない点があるため最終的には量子論的な考察が必要になります．

> 剛体球との衝突と見なすのはあまり適切ではないようです．電気抵抗の温度依存性が正しく導けません．

知らないので教えて欲しいのですが，これは剛体斥力モデルだから温度依存性が出ないのであって，例えば，ソフトコア型等のモデルを考えれば温度依存性が出る，というわけではないのですか?

yama さんのレス (2009/03/09(Mon) 22:50)

ソフトコア型のモデルでは，温度が上がって電子の速さが増すと散乱断面積が減少すると思います．そうすると温度依存性についての実験結果との差は，剛体モデルよりも大きくなると思います． 正しい温度依存性を導くには，たとえば（金属の場合）温度が高くなると散乱断面積が大きくなるようなモデルを考える必要があるでしょう．

nomercy さんのレス (2009/03/09(Mon) 23:42)

>しかし古典論の範囲でも部分的には実験結果に合う結果を導くことができます．

むしろ古典論？の方を良く知らないのですが， この古典的なモデル（平均自由行程＝格子定数）？では 半導体（金属でも良いですが）における電気伝導の何を説明することができたんですか？

yama さんのレス (2009/03/10(Tue) 00:02)

電流密度が電場に比例すること，すなわちオームの法則が導かれるわけです． ただし，電気抵抗の温度依存性は正しく導けません． 特に半導体に対してはこのモデルは不適切でしょう．

nomercy さんのレス (2009/03/10(Tue) 00:29)

オームの法則って緩和時間を導入すれば出てくるわけですよね？ 今は， 「平均自由行程＝格子定数」と，ある程度具体的な値を指定してるわけですから， もう少し定量的なところまで主張できませんか？

yama さんのレス (2009/03/10(Tue) 22:38)

オームの法則が成り立つには，緩和時間が電場方向の平均移動速度に無関係に一定であることが必要です． しかし熱運動を無視して，電場がないときには電子が静止しているとすると，移動速度が電場によって変化すれば緩和時間も変化することになります． しかし熱運動を考えれば，熱運動の速さが圧倒的に大きいため，緩和時間は熱運動の速さによって実質的に決まってしまって，電場方向の移動速度には関係しなくなり，オームの法則が導かれます．

「平均自由行程＝格子定数」は成り立たないと思います．この関係が成り立つと仮定して電気抵抗を計算すれば，実測値と懸け離れたものになるでしょう． 実際の平均自由行程の値を用いても，実測値と１桁違う値となるようです． このモデルは，定量的には不満足なものであり，それ故に量子論的なモデルが必要となるわけです．

digi さんのレス (2009/03/11(Wed) 00:00)

議論の途中ですが．．．

私の質問のほうは解決しました．それどころかどんどん深い話になっているようで，わたしにはついていけそうにありません．でも，おもしろそうな内容なので見させていただいてます．

私が示した移動度の導出方法は簡易的なものですが，実際は量子力学とかを使う必要があるわけですね．ボルツマンの輸送方程式とかいうのがそれにあたるのでしょうか？

>熱運動を考えれば，熱運動の速さが圧倒的に大きいため，．．．

これは電子が流れる速度が非常に遅いことに関係しているのでしょうか？

yama さんのレス (2009/03/11(Wed) 00:06)

>私が示した移動度の導出方法は簡易的なものですが，実際は量子力学とかを使う必要があるわけですね．ボルツマンの輸送方程式とかいうのがそれにあたるのでしょうか？

ボルツマンの輸送方程式は古典論に基づいています．

>これは電子が流れる速度が非常に遅いことに関係しているのでしょうか？

そういうことです．

digi さんのレス (2009/03/12(Thu) 21:12)

みなさん，どうもありがとうございました．

みなさんのお話が聞けて参考になりました（わからないところが多々ありましたが…）．もっと勉強していきたいと思います．

「電気伝導」の記事も読ませていただきます．ありがとうございました！！