量子測定とエネルギー保存則

home > 掲示板 >

このページのPDF版

サイトマップ

量子測定とエネルギー保存則

tohrisugari-san さんの書込 (2009/02/28(Sat) 08:45)

量子測定とエネルギー保存則 tohrisugari-san - 2009/02/26(Thu) 19:38 No.23081 に関するコメントはこちらのスレッドにお願いします．

Re: 量子測定とエネルギー保存則

tohrisugari-san さんのレス (2009/02/28(Sat) 08:55)

mNeji様

２つのコメントありがとうございます．

２つ目のコメント内の「電磁波の固有エネルギ値が直接の観測量になっている」という部分が，よくわかりません．

電磁場の固有エネルギー値を観測するのはどのようにされるのでしょうか？

マクロなコヒーレント状態の電磁場ならば，古典理論と同じになり直接観測できているとなんとなく理解できますが，固有エネルギー値はあくまで量子的効果ですよね．

たぶん全体としておっしゃりたいのは，電磁場はマクロな古典系として振舞うこともできるが，水素原子やと調和振動子はミクロな対象でしかありえない．その観測を行うためには，それらを測るために必要なプローブ系が必要である，自然なプローブは電磁場ではないかというご主張でよろしいでしょうか？

もしそうであれば，同意させて頂きます．

：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：以下記事引用．

Re: 波動関数は測定結果の「設計図」に過ぎないか mNeji - 2009/02/27(Fri) 11:02 No.23088 ▲新規

tohrisugari-sanさん，

興味深く論議を拝見しています．論議とは少し離れた提案をお伝えします．

この掲示版は，一つのスレッドが長くなると，見通しが悪く成りがちです．

まして，複数の論議が並行的に進むと，混乱しがちです．これまでのタイトルだけでも，

・波動関数の浸みこみ効果について・量子測定とエネルギー保存則・波動関数は測定結果の「設計図」に過ぎないか

と変遷してきました．それぞれに，方向を変えた問題意識が示されて来たとおもいます．

とくに「量子測定」はすでに論議済みと思われますが，私に取っては，むしろ「量子測定」は「粒子の位置測定」に限定する方法しか無いのかが疑問です．

そういう意味では，対象モデルの量子力学的な構築と平衡して，例えば電磁場との相互作用をモデル化することも入れて置かないと，論議が噛み合ない様に感じます．

何れにしろ，活発な論議を楽しみにしています．

Re: 波動関数は測定結果の「設計図」に過ぎないか mNeji - 2009/02/28(Sat) 00:25 No.23095 ▲新規

tohrisugari-sanさん，

>「私に取っては，むしろ「量子測定」は「粒子の位置測定」に限定する方法しか無いのかが疑問です．」：この文章は，「位置以外の物理量の測定も議論すべき」というご指摘なのか，それとも他の意図で書かれたことなのでしょうか．もし前者ならば同意見でして，もっと多様な観測量の測定を皆様と論じていければと願っております．

誤解の無い様に，先に申し上げますが，私は量子力学の落ちこぼれです．正統的な理解力はありません．感触に基づいた当てずっぽうをお許し下さい．

さて，上記の意見が出て来た裏側を先に述べますと，「調和振動子モデル」を拝見した時に思い浮かべたのは「プランクの量子仮説」にでてきた調和振動子モデルです．当時，これを見たとき，原子や分子の運動の量子化しか頭の中に無かった私は，一時大混乱しました．

今から見れば，電磁波の量子化では，次の特徴があります；・電磁波の固有エネルギ値が直接の観測量になっている・電磁波自体が熱源との相互作用を組み込んでいる

他方，水素原子の量子化では；・水素原子核と軌道電子とから生みだされる固有エネルギ値は必ずしも，直接されない．・ただし，電荷を持つ為に，電磁波との相互作用は自動的にモデルに内包されている．

そこで，お書きになった「調和振動子モデル」にも，外系との相互作用を明示的に取り込む必要性があるのではないかと考えました．

また，固有エネルギ値に付いてですが，水素原子の例を考えても，基底状態の固有エネルギ値は，原理的にも直接量として観測可能です．例えば，質量分析計で精密測定出来ると思います．所が，励起状態のエネルギ値は，直接観測されていません．そうです，輝線スペクトルは，固有エネルギ準位間のエネルギ差を持ち出した電磁波のエネルギ値の観測，言い換えれば間接的観測量であります．

その類推からすると「調和振動子モデル」で得られた固有エネルギのセットを計算しただけで，その「量子測定」が解明されるのだろうか，そもそも完全孤立系では，純粋固有状態間の遷移が生じないのではないかと，思った次第です．

以上，漠然とした話で済みません．

Re: 量子測定とエネルギー保存則

tohrisugari-san さんのレス (2009/02/28(Sat) 12:19)

ＡＳＡ様

コメントありがとうございます．

確かに連続量である運動量や位置自体の理想測定は近似的に行うのも大変だと思います．

しかし調和振動子のモデルでは，スピンと同じように離散固有値をもつ観測量 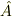$\hat{A}$ を議論しております．

従って連続量の理想測定よりは，実現しやすいと思います．

ただ「何をどのように測定するかを明確にしないといけないかと．」というのは，基本的には同意見です．

一般的には測定モデルの構成（どのような測定器の量子系を持ってくるか，そしてどのような相互作用を調和振動子とさせるかなどの選択）は観測したい物理量に依存します．

しかし一方，有限個の離散的な固有値をもつ一般的な観測量 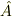$\hat{A}$ の測定については，フォンノイマンのポインター測定という強力な方法があります．

例えば測定器系として１次元無限直線の中を運動する粒子を採用します．通常は運動エネルギーのハミルトニアン

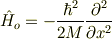
$\hat{H}_o =-\frac{\hbar^2}{2M}\frac{\partial^2}{\partial x^2}$

を考えますが，質量が十分に重くて測定を考える時間スケールでは自由運動は無視できるとします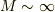．( $M\sim \infty$ )

このため波動関数はこのままでは時間変化せず，動きません．この粒子の位置を「測定器（メータ）の針」（ポインター）と呼びます．

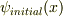そしてその測定器の初期状態を位置空間の中で極めて局在した波動関数にとります．具体的に $x\in [0,\ l]$ の範囲だけ非ゼロをとり，その領域の外では零になっている規格化された波動関数 $\psi_{initial}(x)$ としましょう．

次に物理量 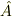$\hat{A}$ を測りたい調和振動子の系と，その測定器系の相互作用を次のように致します．

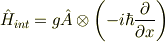
$\hat{H}_{int}=g \hat{A}\otimes\left(-i\hbar\frac{\partial}{\partial x} \right)$

は相互作用の結合定数で実数です．

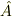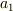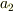以下では簡単のために物理量 $\hat{A}$ の異なる固有値は a_1 と a_2 の２つだとします．もちろん対応する固有状態は多重度の縮退をしており，異なる固有関数でも同じ固有値を持っている場合がたくさんあります．

簡単のために調和振動子系の状態が

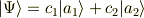
$|\Psi\rangle=c_1 |a_1\rangle+c_2 |a_2\rangle$

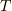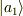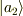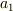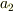であるときに，時間の間だけ上記の相互作用を測定器と行うとします．ここで $|a_1 \rangle$ ， $|a_2\rangle$ は固有値 a_1 ， a_2 をもつ，ある固有状態です．

合成系の状態は調和振動子の状態と測定器の状態のテンソル積で書けて，測定前には

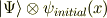
$|\Psi\rangle \otimes \psi_{initial}(x)$

となっています．

相互作用のハミルトニアンから生成される時間発展演算子は

$U(T)=\exp\left[-i\frac{T}{\hbar}\hat{H}_{int} \right]$

で書けます．

従って測定器との相互作用による時間発展は

$U(T)\left(|\Psi\rangle\otimes \psi_{initial}(x) \right)=\exp\left[-\frac{gT}{\hbar}\hat{A}\otimes\frac{\partial}{\partial x} \right]\left(c_1 |a_1\rangle \otimes \psi_{initial}(x) +c_2 |a_2\rangle\otimes\psi_{initial}(x)\right)$

となります．

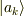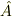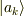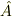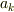さらに $|a_k\rangle$ は演算子 $\hat{A}$ の固有状態ですから，演算作用の際に $|a_k\rangle$ にタッチする $\hat{A}$ は a_k という固有値に置き換えることができます．このことは計算を以下のように楽にします．

$U(T)\left(|\Psi\rangle\otimes \psi_{initial}(x) \right)=c_1 \exp\left[-\frac{gT}{\hbar}a_1 \frac{\partial}{\partial x} \right]|a_1\rangle \otimes \psi_{initial}(x) +c_2 \exp\left[-\frac{gT}{\hbar}a_2 \frac{\partial}{\partial x} \right]|a_2\rangle\otimes\psi_{initial}(x)$

そして

$\exp\left[-\Delta \frac{\partial}{\partial x} \right]f(x)=f\left(x-\Delta\right)$

という公式を思い出すと，

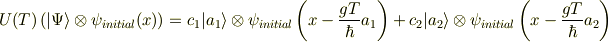
$U(T)\left(|\Psi\rangle\otimes \psi_{initial}(x) \right)=c_1 |a_1\rangle \otimes \psi_{initial}\left(x -\frac{gT}{\hbar}a_1\right) +c_2 |a_2\rangle\otimes\psi_{initial} \left(x -\frac{gT}{\hbar}a_2\right)$

という結果が得られます．

この結果は大変面白いです．パラメータ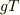を大きくすると，測定器の波動関数が局在する場所が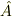， $\hat{A}$ の固有値ごとに離れて行きます．この距離間隔をマクロな大きさ 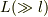$L(\gg l)$ まで引き離すように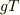を設定しましょう．（これが測定情報の信号増幅過程にあたります．前に頂いたコメントでは，乾板上での化学反応に対応しています．）

このため，２つの測定器の波動関数は互いに直交します：

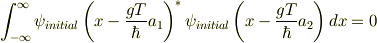
$\int^\infty_{-\infty} \psi_{initial}\left(x -\frac{gT}{\hbar}a_1\right)^\ast\psi_{initial}\left(x -\frac{gT}{\hbar}a_2\right)dx=0$

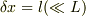測定結果はすでにマクロ化していますので，測定器のを測定すれば $\delta x=l(\ll L)$ 程度の誤差で容易に

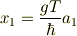
$x_1 =\frac{gT}{\hbar}a_1$

または

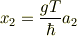
$x_2 =\frac{gT}{\hbar}a_2$

のどちらかの位置に観測されるはずです．

その位置の値で知りたかった調和振動子の物理量 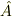$\hat{A}$ の値が読み取れます:

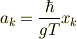
$a_k =\frac{\hbar}{gT} x_k$

ここで重要なこととして以下のことがあります．得られた量子状態：

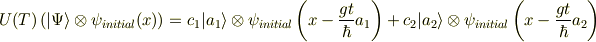
$U(T)\left(|\Psi\rangle\otimes \psi_{initial}(x) \right)=c_1 |a_1\rangle \otimes \psi_{initial}\left(x -\frac{gt}{\hbar}a_1\right) +c_2 |a_2\rangle\otimes \psi_{initial}\left(x -\frac{gt}{\hbar}a_2\right)$

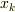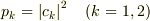から，ちょうど各々の x_k の値が $p_k =\left|c_k \right|^2\ \ \ (k=1,2)$ という確率で現れることがわかります．

この確率はもとの調和振動子の状態：

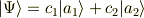
$|\Psi\rangle=c_1 |a_1\rangle+c_2 |a_2\rangle$

において 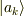$|a_k\rangle$ が観測される確率と一致しております．

従ってこの事実から，この測定器モデルは先に述べた条件をもつ一般的な物理量 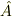$\hat{A}$ の理想測定モデルになっていると考えられるわけです．

この議論からわかるように，わりと一般的な物理量を同一測定モデルで解析できることは知られています．

ですから，測る物理量を変えるたびに測定器モデルも必ず変える必要はないと思います．

：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：以下記事引用： Re: 波動関数は測定結果の「設計図」に過ぎないか ASA - 2009/02/28(Sat) 08:46 No.23100 新規

tohrisugari-sanさん >限りなく理想測定に近い実験は可能です．たとえば有名な電子スピンを測定するシュテルンとゲルラッハの実験なんか理想測定に近いものと言えます．そりゃ，エネルギーと同時固有値をもつようなスピン測定なら，問題は少ないですよ．その場合は，観測されるエネルギーはE0で変らないので，<E>＞E0の定理が成立しない．問題なのは，運動量測定のような場合で，ご存知のように運動量固有状態は，平面波なので，位置x→∞でもnon0．x→∞で0になる束縛状態とは様子が全く違う．測定でポテンシャルを破壊すると考えるか．もしくは，ポテンシャルがそのままなら，平面波の<V>は発散してるので，測定器が無限大のエネルギーを与えないといけなくなる．どちらの考えにせよ，現実離れしているように思えます．このようなことから，量子測定関連の議論は，安易に物理量Aと一般化できないように感じてます．何をどのように測定するかを明確にしないといけないかと．

mNejiさん >完全孤立系では，純粋固有状態間の遷移が生じないのではないかと被測定糸と測定系をmixした量子系を考えるべきということでしょうか？どっかでselection(収縮)を適用するのだから，どこかで境界ができますよ．いきなり複雑なモデルにすると，わけが判らなくなるような気がします．

あと，単一水素原子モデルで電磁波ありを考えても，特定エネルギーの電磁波しか関係しませんよね．関係する電磁波があると，定常状態でなくていわゆる重ね合わせ状態なので，特定の電磁波を吸い取った状態，もしくは，吐き出している状態が観測されるわけです．

Re: 量子測定とエネルギー保存則

ASA さんのレス (2009/02/28(Sat) 21:43)

tohrisugari-sanさん初めの問題では，位置測定が絡んだ話だったので，一般的物理量Aとして連続固有値を持つケースをも包含しているのかなと思いました．なので確認の意味でコメントいたしました．このように連続固有値をもつケースでは，ご紹介のようなポインター測定方法は，適切でないですよね．

>調和振動子のモデルでは，スピンと同じように離散固有値をもつ観測量を議論しております．要するにスピンのようなものを前提とするわけですね．ご紹介の話は，磁場かけて，変位量からスピンを振り分けることに対応してますね．

>測る物理量を変えるたびに測定器モデルも必ず変える必要はないと思います．同質なものだったらOKですが，当初の位置測定を考えておられるなら別のモデルに変える必要があると思います(どんなモデル適切であるかは，知見が不足しておりますのでコメントできません)．

Re: 量子測定とエネルギー保存則

mNeji さんのレス (2009/02/28(Sat) 22:36)

どこに返信すれば良いか判らないので，取り敢えず，ここにコメントさせて頂きます．

＞フォンノイマンのポインター測定という強力な方法

の概説を眺めさせていただきました．大昔，「ボームの量子力学で隠れた変数」といった扱いがあったように朧げに思い出しました．計測系の進歩や半導体デバイス技術を背景に，量子力学の基礎論的な見直しがされているのだろう，と感じました．

残念な事に，柔軟な思考能力が欠如している自分には，到底論議の対象にならない事が判りました．

是非とも，明確な解釈が進展される事を期待します．

Re: 量子測定とエネルギー保存則

グッドラックさんのレス (2009/03/01(Sun) 09:36)

どうもです．全部目を通してやっと追いつきましたが，結構見当違いなレスがtohrisugari-sanさんに戻って気の毒ですよね．ちょっとここの掲示板ではこの話題は荷が重いのではないかと私も感じます．tohrisugari-sanさんのvon Neumannのpointer basisの話は「ボームの量子力学で隠れた変数」とは全く関係ないし．変な人と間違われてるんじゃないのかな．柔軟な思考能力ってのもtohrisugari-sanさんの記事を読むのに必要ですかね．結構丁寧に書かれているように思えます．正統派的に自分には見えますけどね．

Re: 量子測定とエネルギー保存則

tohrisugari-san さんのレス (2009/03/01(Sun) 19:12)

ＡＳＡ様

「このように連続固有値をもつケースでは，ご紹介のようなポインター測定方法は，適切でないですよね．」というコメントに関してです．

測定器のメータの初期量子状態をデルタ関数に比例するような極限関数にとれるならば，フォンノイマンのポインター測定によっても位置の理想測定が達成できますが，これは現実的に難しいと思います．

＝＞皆様，この一連のスレッドに関しては十分に議論して頂きましたので，一旦ここで打ち切りたいと思います．ありがとうございました．

Re: 量子測定とエネルギー保存則

toorisugari no Hiro さんのレス (2009/03/02(Mon) 15:39)

> 皆様，この一連のスレッドに関しては十分に議論して頂きましたので，一旦ここで打ち切りたいと思います．ありがとうございました．

スレ主さんがやめられたので，議論が続けようがないですが，私の疑問は晴れません．

古典的禁止領域で粒子が観測されるのか?されるとして，それは，観測装置のためにエネルギーが注入されるなどしてポテンシャルが変わったためでないのか．

トンネル効果を観測しているだけでないのかとの疑問は晴れません．

装置をsetして起動したことで，(粒子をとばさなくても)ポテンシャルが変化しますが，この可能性を上手に回避した実験はないのでしょうか．

例えば，コンデンサーを使って減速されるような電場に遠方から荷電粒子を走らせ，コンデンサの後ろに銀盤等を置いて反応させる実験を考えます．

電位を荷電粒子のエネルギーより高くとると，コンデンサーの後ろは古典的禁止領域になります．

このとき，仮に銀盤に反応があったとしても，「事実上のトンネル効果だから」と「古典的禁止領域での粒子の観測」を否定できます．

「事実上のトンネル効果だから」を否定する(回避する)にはどうしたらよいのでしょう．

考えたのは，ゲートとなるコンデンサの電位を上げていくという方法です．装置をおいたことで静的なポテンシャルが変化したためトンネル効果で観測されたのなら，電位を上げることで，観測される頻度が， (1)変形されたポテンシャルにおけるトンネル効果で計算される頻度 (2)元のポテンシャルで計算される頻度のどちらに従うかの違いが出るはずです．

# 装置をおいて起動したことで有限のエネルギーが与えられるために観測されるなら，それより高いエネルギー障壁ならどうなるか?ということです．

これは，光を当てることで観測する場合には，周波数で決まるエネルギーより高い障壁ではどうなるかという問です．

これらの実験の結果(もっと良い実験があれば，そちらを)ご存じの方はいませんか?

[home] [掲示板] [ページの先頭]