4次元球の表面積
4次元球の表面積
トビラ.. さんの書込 (2009/02/24(Tue) 00:34)
みなさん,こんばんわん!
4次元Euclid空間中の球の表面積についてなのですが,本では 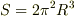 となって,結果だけをのせています.どのように導出したのかわからなくて困っているんですけども,一応自分でも努力して解いてみたので,ご指摘やアドバイスをお願いします.
まず,4次元Euclid空間内で半径
となって,結果だけをのせています.どのように導出したのかわからなくて困っているんですけども,一応自分でも努力して解いてみたので,ご指摘やアドバイスをお願いします.
まず,4次元Euclid空間内で半径  の球の方程式を
の球の方程式を 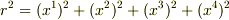 と定義します.
そこで,4次元の極座標変換を考えてみます.
4次元の極座標変換は2次元と3次元の類推により
と定義します.
そこで,4次元の極座標変換を考えてみます.
4次元の極座標変換は2次元と3次元の類推により
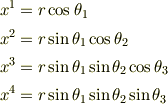
とおきます.多分ですがこれを用いて4元線素 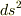 を計算すると
を計算すると
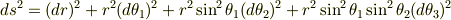
となると思います.
したがって4元体積要素 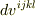 は
は
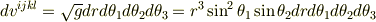
となると思うので,ここで,積分範囲は 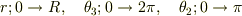 と3次元の極座標の類推により考えられると思います.
と3次元の極座標の類推により考えられると思います. 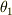 の積分範囲については予測できないので
の積分範囲については予測できないので 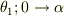 として4次元球の体積
として4次元球の体積  を計算すると
を計算すると
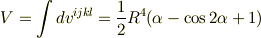
となるのでこの球の表面積  は
は
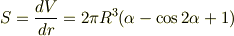
となります.ここで,答えは 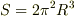 とわかっているので
とわかっているので 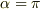 であることが理解できます.
この考え方はあっているのでしょうか?また,もしあっていたとしたならばなぜ,
であることが理解できます.
この考え方はあっているのでしょうか?また,もしあっていたとしたならばなぜ, 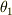 の積分範囲が
の積分範囲が 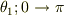 となるのでしょうか?
どうかアドバイスやご指摘(できれば解答)お願いします.
となるのでしょうか?
どうかアドバイスやご指摘(できれば解答)お願いします.
Re: 4次元球の表面積
yama さんのレス (2009/02/24(Tue) 11:28)
それで合っていると思います.
積分範囲については, 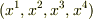 と
と 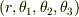 が原点を除いて1対1に対応するように決めればそのようになると思います.
たとえば,もし,
が原点を除いて1対1に対応するように決めればそのようになると思います.
たとえば,もし, 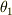 の積分範囲が
の積分範囲が 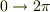 であれば
であれば  もこの範囲に入ります.このとき
もこの範囲に入ります.このとき 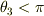 であれば,
であれば, 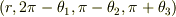 と
と 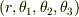 が同一の
が同一の 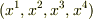 に対応してしまいます.
に対応してしまいます.
Re: 4次元球の表面積
Yokkun さんのレス (2009/02/24(Tue) 12:11)
トビラ..さん,こんにちは.
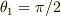 は,
は, 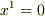 すなわち
すなわち 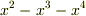 超平面(3次元ユークリッド空間)を表しますね.この超平面を境界として4次元空間が
超平面(3次元ユークリッド空間)を表しますね.この超平面を境界として4次元空間が 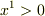 と
と 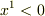 に2分されます.この2領域に対応する座標は,
に2分されます.この2領域に対応する座標は, 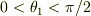 と
と 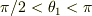 ですよね?
ですよね?
4次元超球の表面積については,検索でけっこうよい解説がひっかかってきます.
→結果がまちがってますが,わかりやすい説明と思います.他に
など.
Re: 4次元球の表面積
トビラ.. さんのレス (2009/02/24(Tue) 22:53)
yamaさんYokkunさんどうもありがとうございます.
Yokkunさんへ
ここで質問する前にネットで調べるのを忘れてました.すみません.特に2番目のサイト(?)が数学的に詳しく計算してあってすごく気に入りました.直行直線座標で4次元空間の球の表面積を求める方法は思いつきませんでした.
ありがとうございます.
また,積分範囲のことについてなのですが,なるほど,二分されるから4次元空間を考えたさい 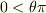 の範囲が最低必要な領域(?)ということでしょうか?
の範囲が最低必要な領域(?)ということでしょうか?
yamaさんへ
積分域についてとても興味深いことを聞き参考になりました.ありがとうございます.
しかしながら,僕の理解力の乏しさゆえ少しばかり理解できませんでした.
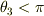 と書かれていますが,そうでなくてもすべて1対1に対応するのではないのでしょうか?
だとすると
と書かれていますが,そうでなくてもすべて1対1に対応するのではないのでしょうか?
だとすると 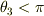 という条件はどこから来たのでしょうか?
という条件はどこから来たのでしょうか?
Re: 4次元球の表面積
yama さんのレス (2009/02/25(Wed) 00:24)
の場合は
が
を超えるからです.
その場合は, 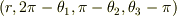 と
と 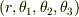 が同一の
が同一の 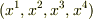 に対応します.
いずれにしても
に対応します.
いずれにしても 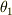 の積分範囲が
の積分範囲が 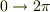 であれば,
であれば, 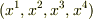 と
と 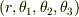 の対応が1対1でなくなるので,1対1にするためには
の対応が1対1でなくなるので,1対1にするためには 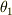 の積分範囲を
の積分範囲を 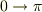 に制限しなければならないわけです.
に制限しなければならないわけです.
Re: 4次元球の表面積
Yokkun さんのレス (2009/02/25(Wed) 10:05)
ユークリッド空間ですから,直交座標が圧倒的に見通しがいいわけですね.その見通しのよさと球対称領域の積分という課題の折り合いをつけるということになります.
幾何学的なイメージにこだわってみたいのですが,(以下不等号は一部必要な等号をのぞいていますが,ご勘弁を)
3次元極座標における2つの角座標 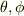 の役割の違いを考えてみてください.
空間をくまなく張る手順に2通り考えられます.
(1)
の役割の違いを考えてみてください.
空間をくまなく張る手順に2通り考えられます.
(1) 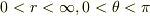 で定義される半平面を
で定義される半平面を 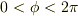 にわたり回転させる.
(2)
にわたり回転させる.
(2) 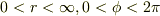 で定義される円錐面を
で定義される円錐面を 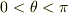 にわたって開き角を動かす.
(他に
にわたって開き角を動かす.
(他に 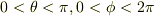 で定義される球面を
で定義される球面を 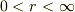 にわたって動かす手順もあります.)
にわたって動かす手順もあります.)
4次元の場合は,トビラ..さんの定義では 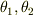 が3次元の
が3次元の  と同じ役割で,
と同じ役割で, 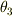 が3次元の
が3次元の  と同じ役割をしています.すなわち,
(1)
と同じ役割をしています.すなわち,
(1) 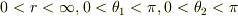 によって定義される半超平面(
によって定義される半超平面( 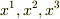 の3軸によって張られる3次元空間のうち
の3軸によって張られる3次元空間のうち 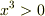 の領域)を
の領域)を 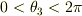 にわたって回転させる.
(2)
にわたって回転させる.
(2) 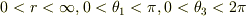 によって定義される超円錐面を
によって定義される超円錐面を 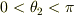 にわたって開き角を動かす.
(その他いくつか考えられます.)
・・・という具合.ちょっとわかりにくいですが,3次元との類推をフルに働かせればイメージできそう?
にわたって開き角を動かす.
(その他いくつか考えられます.)
・・・という具合.ちょっとわかりにくいですが,3次元との類推をフルに働かせればイメージできそう?
Re: 4次元球の表面積
トビラ.. さんのレス (2009/02/25(Wed) 11:26)
yamaさんどうもありがとうございました.
どうにか理解できました.つまりは 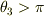 だと
だと 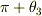 が
が 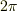 以上になってしまい,1周してしまうので1対1に対応でなくなるということですよね.その場合(
以上になってしまい,1周してしまうので1対1に対応でなくなるということですよね.その場合( 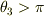 )は
)は 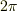 を超えないように
を超えないように 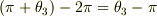 と調整する必要があるわけですね.
でも,よく考えたら確かに
と調整する必要があるわけですね.
でも,よく考えたら確かに 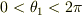 だと1対1に対応しなくなるから
だと1対1に対応しなくなるから 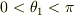 とする必要があるけど,そうしたらまた積分範囲が違ってきてくるので(
とする必要があるけど,そうしたらまた積分範囲が違ってきてくるので( 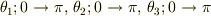 と積分範囲がなるから),その積分範囲では計算があわないのでどうしたらいいのでしょうか?
と積分範囲がなるから),その積分範囲では計算があわないのでどうしたらいいのでしょうか?
Yokkunさん,なるほど,そのように幾何学的(?)に考えればそれ以上の高次元に対しても  となることが予測できますね.
どうもありがとうございました.
となることが予測できますね.
どうもありがとうございました.
Re: 4次元球の表面積
yama さんのレス (2009/02/25(Wed) 23:48)
の積分範囲は
とするわけです.
Re: 4次元球の表面積
トビラ.. さんのレス (2009/02/26(Thu) 22:10)
yamaさんありがとうございます. 何とか理解できました.僕にとっては少し難しかったですが大変勉強にさせてもらいました. どうもありがとうございました.
Re: 4次元球の表面積
mNeji さんのレス (2009/02/27(Fri) 06:30)
トビラ..さん,
横から失礼します.興味深く拝見いたしました.
自分のように数学的なセンスがないものとして,初めて「4次元球」をイメージできたような気がして面白かったです.
できれば絵をつけた解説をお造り戴けると,これから勉強をされる方々にも参考にある様な気がします.「物理のかぎしっぽプロジェクト」に加入されて記事にするのも一法かもしれませんね.
Re: 4次元球の表面積
トビラ.. さんのレス (2009/02/27(Fri) 15:14)
mNejiさん,物理のかぎ尻尾プロジェクトへのおさそいありがとうございます. 僕も前々からこの素敵なプロジェクトに参加したいとは思ってはいたのですが,自分の勉強に手いっぱいなので断念した所存でございます. もっと力をつけて指導できる立場になったときにはいつか参加してみようと思っています. これからも死ぬまで真実一路邁進していこうと心中に考えます. なのでここにはたびたびお世話になりますが,これからもよろしくお願いします.