2次元のクーロンの法則
2次元のクーロンの法則
digi さんの書込 (2009/02/23(Mon) 00:38)
簡単な質問かもしれませんが.
3次元では電磁気力は距離の逆2乗に比例しますが,2次元ではそうはならないようなのですが,これはどうしてでしょうか?2次元では,2個の電荷q1,q2があるときの電界,電位,力はどのようになりますか?
自分なりに考えてみたところ,電界は
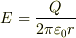 となるのではないかと思います.でも,これだと電位が定義されません.
ご指導おねがいします.
となるのではないかと思います.でも,これだと電位が定義されません.
ご指導おねがいします.
Re: 2次元のクーロンの法則
Yokkun さんのレス (2009/02/23(Mon) 09:58)
もし,空間が2次元だったら・・・という話でしょうか?
静電気の範囲で,最も基本的な法則は「ガウスの法則」でしょうから,
3次元では, 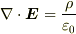 2次元では,
2次元では, 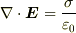 となると仮定したわけですね?
すると,積分形は
となると仮定したわけですね?
すると,積分形は
 閉曲線
閉曲線 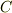 を半径
を半径  の円にとれば,ただちに
の円にとれば,ただちに
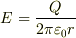 すると電位は,基準点を
すると電位は,基準点を 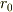 として,
として,
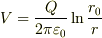 となりそうですね.実際電位のこの形は,3次元でも円筒対称な電荷分布において現れる形です.
となりそうですね.実際電位のこの形は,3次元でも円筒対称な電荷分布において現れる形です.
問題が電流や磁場を含む電磁場になると,とたんに2次元世界の電磁気学は破綻しそうですね.^^;
Re: 2次元のクーロンの法則
digi さんのレス (2009/02/23(Mon) 11:39)
お返事ありがとうございます.
2次元での電界分布や電気力線がどうなるかを考えていて,クーロンの法則などが3次元で距離の逆2乗に比例するのに対して,2次元ではそうはならないと知りました.ということは,たとえば2個の電荷がある空間を考えて,両電荷を通る平面で空間を切ったときその断面での電気力線の形などは3次元で考えられる理論とは違う形になるのでしょうか?
Re: 2次元のクーロンの法則
toorisugari no Hiro さんのレス (2009/02/23(Mon) 15:23)
Yokkunさんがおっしゃるように,2次元の電場は  方向に一様な電荷分布において現れる3次元の電場と同形です.
方向に一様な電荷分布において現れる3次元の電場と同形です.
> 両電荷を通る平面で空間を切ったときその断面での電気力線の形などは3次元で考えられる理論とは違う形になるのでしょうか?
二つの点電荷が作る3次元電場と,二つの平行な直線上に並んだ電荷が作る3次元電場とは同じでしょうか?
Re: 2次元のクーロンの法則
digi さんのレス (2009/02/23(Mon) 18:11)
>二つの点電荷が作る3次元電場と,二つの平行な直線上に並んだ電荷が作る3次元電場とは同じでしょうか?
違います.
>2次元の電場はz方向に一様な電荷分布において現れる3次元の電場と同形です.
しつこいかもしれませんが,2次元の電場が (1)2個の電荷がある空間を考えて,両電荷を通る平面で空間を切ったときその断面 (2)z方向に一様な電荷分布において現れる3次元の電場と同形 (1)ではなく(2)となるのはどうしてでしょうか?
Re: 2次元のクーロンの法則
toorisugari no Hiro さんのレス (2009/02/23(Mon) 18:22)
> しつこいかもしれませんが,2次元の電場が (1)2個の電荷がある空間を考えて,両電荷を通る平面で空間を切ったときその断面 (2)z方向に一様な電荷分布において現れる3次元の電場と同形 (1)ではなく(2)となるのはどうしてでしょうか?
電気力線がどう分布するか考えてみましたか?
電気力線は互いにできるだけ距離を取るように,かつ,力線の長さが短くなるように分布します.力線の3次元分布が違うのに,何故,2次元断面の力線分布が等しいと思えるのでしょうか?
Re: 2次元のクーロンの法則
Yokkun さんのレス (2009/02/23(Mon) 19:14)
花火の火球がひろがるのをイメージしてください.3次元では球状に広がりますよね?2次元では円状に広がります.火球の数が両者で等しければ,どうなるか考えてください.ガウスの法則(またはクーロンの法則)は,電荷  から出る電気力線が
から出る電気力線が 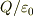 本であることを述べています.「火球」の数が電荷によって決まっているわけです.そして,電場の強さは単位面積を垂直につらぬく電気力線の数に等しいというわけです.2次元では力線に垂直な単位面積が取れませんから,単位長あたりということになるでしょう.3次元の場合に厚さを1にとったものと考えればいいと思います.
本であることを述べています.「火球」の数が電荷によって決まっているわけです.そして,電場の強さは単位面積を垂直につらぬく電気力線の数に等しいというわけです.2次元では力線に垂直な単位面積が取れませんから,単位長あたりということになるでしょう.3次元の場合に厚さを1にとったものと考えればいいと思います.
Re: 2次元のクーロンの法則
digi さんのレス (2009/02/25(Wed) 13:05)
(1)2個の電荷がある空間を考えて,両電荷を通る平面で空間を切ったときその断面 (2)z方向に一様な電荷分布において現れる3次元の電場と同形
(1)と(2)では明らかに電気力線の数や形が違うということでしょうか?
Re: 2次元のクーロンの法則
toorisugari no Hiro さんのレス (2009/02/25(Wed) 13:56)
> しつこいかもしれませんが,2次元の電場が (1)2個の電荷がある空間を考えて,両電荷を通る平面で空間を切ったときその断面 (2)z方向に一様な電荷分布において現れる3次元の電場と同形 (1)ではなく(2)となるのはどうしてでしょうか?
2次元の電場を3次元の電場の断面で定義する場合,元となる3次元の電場は
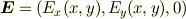
という「2次元への制限形」をしていなければいけません.また,3次元電荷分布も「2次元への制限形」 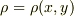 ,つまり,電荷はz方向に一様に分布してなければいけません.
,つまり,電荷はz方向に一様に分布してなければいけません.
以下の式を2次元への制限とよびます.
(1) スカラー場 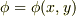 (2) 3次元ベクトル場
(2) 3次元ベクトル場 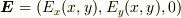 (3) 3次元擬ベクトル場
(3) 3次元擬ベクトル場 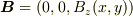 (4) 密度場
(4) 密度場 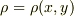
2次元の場を3次元の場の断面で定義する場合,元となる3次元の場がこの制限の規則を守らないと,2次元版支配方程式を2次元の場は満しません.
このことをガウスの法則の2次元版で考えましょう.
電荷  の点電荷
の点電荷 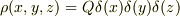 が作る3次元電場
が作る3次元電場
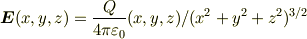
は2次元への制限形をしていません.ですから,平面( 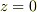 )での断面を取ることで得られる2次元電場
)での断面を取ることで得られる2次元電場
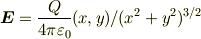
では,ガウスの法則の2次元版を満足できません.これを直接計算で確かめてもよいですが,以下のように考えても示せます.
電荷がない場所では電場の発散は0になるはずです.しかし,平面( 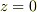 )上では
)上では 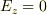 ですが
ですが 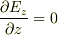 ではないので,
ではないので,
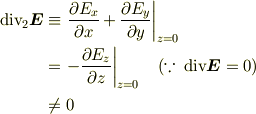
となり,ガウスの法則の2次元版を破ります.
一方,z方向に一様で単位長さあたりの電荷  の電荷分布
の電荷分布 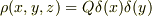 が作る3次元電場
が作る3次元電場
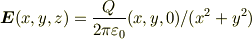
は2次元への制限形をしているので 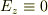 ,つまり,
,つまり, 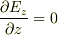 を満たします.よって,これから得られた2次元電場
を満たします.よって,これから得られた2次元電場
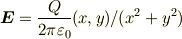
は真空中でのガウスの法則の2次元版
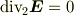
を満足します.
以上は静電場を記述する方程式の一つであるガウスの法則 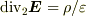 について検証しましたが,もう一つの条件(静電ポテンシャルが存在する条件)である
について検証しましたが,もう一つの条件(静電ポテンシャルが存在する条件)である
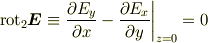
についても検証する必要があります.余力があればやってみてください.
Re: 2次元のクーロンの法則
digi さんのレス (2009/02/27(Fri) 16:34)
Yokkunさん,花火を例に説明してくださってありがとうございます.参考になりました.
toorisugari no Hiroさん,最後にかなりくわしく説明したいただき非常に勉強になりました.静電ポテンシャルが存在する条件のほうも考えてみます!
ありがとうございました!!