エネルギーと時間の不確定性関係について
エネルギーと時間の不確定性関係について
グッドラック さんの書込 (2009/02/22(Sun) 09:21)
mNejiさんの 2009/02/21(Sat) 23:14 No.23000の記事でちょうど「エネルギーと時間の不確定性関係」が出てきて,反応しました.量子力学を勉強しているとき違和感があったのを思い出します.例えば位置と運動量の不確定性関係は観測値の平均2乗誤差を定義して厳密に証明できました.しかしエネルギーと時間の関係になるとなんか曖昧なことしか学ばなかった気がします.例えばエネルギーは物理量でいいのですが,時間って物理量なのかということもよくわかりませんでした.湯川さんの中間子論での応用とかは解説ありましたが,厳密な定義や証明は自分は見てなかったですね.
エネルギーと時間の不確定性関係についてどなたか教えてくださいませんか?
Re: エネルギーと時間の不確定性関係について
mNeji さんのレス (2009/02/22(Sun) 10:43)
グッドラックさん,
元記事には訂正意見をお書きしました.このご質問に詳しい説明をできないので,多の識者の方々の解説をお待ち下さい.
Re: エネルギーと時間の不確定性関係について
tohrisugari-san さんのレス (2009/02/24(Tue) 13:37)
パウリ(だったか?)の定理というものがあります.
定理:ある量子系にハミルトニアン 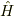 と正準共役で,かつエルミートな時間演算子
と正準共役で,かつエルミートな時間演算子 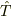 が存在する場合,ハミルトニアンの固有値は連続値で
が存在する場合,ハミルトニアンの固有値は連続値で 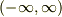 の領域のすべての値をとる.
の領域のすべての値をとる.
つまりハミルトニアンが特別な性質を持たないと物理的時間演算子は存在しないという内容です.
証明は次のような感じです.
![[\hat{H},\ \hat{T}]=i\hbar](http://hooktail.maxwell.jp/bbslog/af96839829a41ccba7c4a7bb6b488105.png) を満たすエルミート演算子
を満たすエルミート演算子 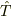 が存在するとします.
が存在するとします.
そして 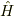 の1つの固有状態
の1つの固有状態 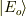 (固有値を
(固有値を 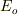 とします.)を考えます.
とします.)を考えます.
そして次の1つの実パラメタ 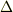 (
( 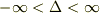 )に依存した次のユニタリ変換
)に依存した次のユニタリ変換
![U(\Delta)=\exp\left[-i\frac{\Delta}{\hbar}\hat{T}\right]](http://hooktail.maxwell.jp/bbslog/ace212337e9834decac6a4173d2a8ccf.png)
を定義します.
この変換には
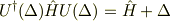
という性質があります.(運動量演算子 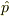 から
から ![\exp\left[-i\frac{a}{\hbar}\hat{p}\right]](http://hooktail.maxwell.jp/bbslog/c28fd01b2d8fe92e28adfed0805106d4.png) を作ってやると,位置の推進ユニタリ変換が生成できるのと同じ証明となります.)
を作ってやると,位置の推進ユニタリ変換が生成できるのと同じ証明となります.)
この関係から
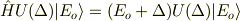
という関係を得ることができるため, 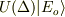 がハミルトニアンの固有値
がハミルトニアンの固有値 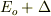 をもつ固有状態であることがわかります.固有値
をもつ固有状態であることがわかります.固有値 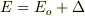 は
は 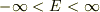 の領域のすべての値をとることになり,証明が終わります.
の領域のすべての値をとることになり,証明が終わります.
このようなことが実現する例の1つは坂を転がり続ける粒子です.例えばポテンシャルが  を非ゼロの実定数として
を非ゼロの実定数として
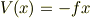
という形をしている場合には時間演算子を構成できます.(その具体形は練習問題としてとっておきます.)
従ってこのような例では時間とエネルギーに関する厳密な不確定性不等式:
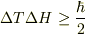 が任意の量子状態に対して成り立ちます.
が任意の量子状態に対して成り立ちます.
Re: エネルギーと時間の不確定性関係について
naruheso さんのレス (2009/02/25(Wed) 08:12)
tohrisugari-sanさん(って,さんが重なってしまう)
時間演算子の記事,興味深いです.でもこの時間って,波動関数に現れるパラメータとしての時間とは異なる概念ですよね.一般に量子力学では(少なくとも非相対論的なバージョンのものでは)時間は物理量ではないですよね.特定の系で時間演算子があるとしても,シュレーディンガー方程式とかに現れる時間パラメータとの関連はどのようになっているのでしょうね.
Re: エネルギーと時間の不確定性関係について
tohrisugari-san さんのレス (2009/02/25(Wed) 21:34)
naruheso様
この時間演算子はもちろん波動関数のひき数に現れる時間パラメタとは概念的にも異なるものです.時間演算子は考えている系ごとに特定の物理的意味づけをされる「時間間隔」を表すものと考えられます.
例えば坂をころがる粒子のモデルでは,運動量がゼロになる時刻から今現在までの時間差という意味がある時間演算子を作ることができます.少し丁寧に書いてみます.
ハミルトニアンは
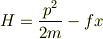
で与えられます.  は正の値としましょう.
は正の値としましょう.
まず古典力学としてこの問題を解きますと,運動量は
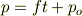
のように得られます.ここで 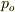 は時刻
は時刻  での運動量の値です.これは一定の力が粒子にかかり続けるモデルであることから,解かずともわかる事実です.
での運動量の値です.これは一定の力が粒子にかかり続けるモデルであることから,解かずともわかる事実です.
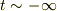 の過去には,粒子はマイナス方向の運動量をもって粒子は左向きにすごい速さで走ってましたが,右向きの一定の力を受け続けて時刻
の過去には,粒子はマイナス方向の運動量をもって粒子は左向きにすごい速さで走ってましたが,右向きの一定の力を受け続けて時刻 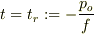 において運動量がついに零になります.この
において運動量がついに零になります.この 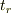 を使うと先ほどの解は
を使うと先ほどの解は
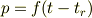
とも書くことができます. 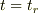 の後も力はかかり続けるため,粒子は右向きの運動量を持ち始め速度を速めていきます.これが古典運動です.
の後も力はかかり続けるため,粒子は右向きの運動量を持ち始め速度を速めていきます.これが古典運動です.
次に量子化したときの時間演算子を考えてみます. ![[\hat{H},\ \hat{T}]=i\hbar](http://hooktail.maxwell.jp/bbslog/af96839829a41ccba7c4a7bb6b488105.png) を満たすエルミート演算子
を満たすエルミート演算子 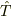 として
として
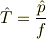
というものが存在します.(もちろんこれ以外にも実関数 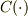 を使って定義される
を使って定義される
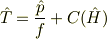
も問題の交換関係を満たすエルミート演算子ですが,今回は簡単のために置いておきます.)
ハイゼンベルグ方程式を解くと
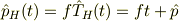
となりますので,
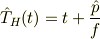
という関係を得ます.( ![\hat{O}_H (t)=\exp\left[i\frac{t\hat{H}}{\hbar}\right]\hat{O}\exp\left[-i\frac{t\hat{H}}{\hbar}\right]](http://hooktail.maxwell.jp/bbslog/924db1399fd5c0ed37027eae190d3b7e.png) )
)
古典解との対応で,
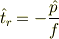
という演算子を導入すると
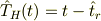
という関係になります.時間に依存しないシュレーディンガー表示の演算子である 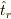 は古典解との類推から,粒子の運動量が力を受けてちょうど零になった時刻を表現するエルミート演算子と解釈できます.従ってこの時間演算子のハイゼンベルグ演算子は,粒子の運動量が零になった時刻から今考えている時刻
は古典解との類推から,粒子の運動量が力を受けてちょうど零になった時刻を表現するエルミート演算子と解釈できます.従ってこの時間演算子のハイゼンベルグ演算子は,粒子の運動量が零になった時刻から今考えている時刻  までに流れた時間という物理的意味を持つことがわかります.
までに流れた時間という物理的意味を持つことがわかります.
Re: エネルギーと時間の不確定性関係について
naruheso さんのレス (2009/02/26(Thu) 07:52)
丁寧なコメント,サンキュです.
素粒子レベルで知られている相互作用に基づいたハミルトニアンは系の安定性の要請から「下に有界な固有値スペクトラム」を持つので,厳密な意味での時間演算子はないと考えられる.ので,転がり続ける粒子モデルも坂の底についたら時間演算子の性質は壊れますよね.それでも,モデルの適用範囲の中で物理的に意味のある時間演算子ができるという点では面白いと思う.
Re: エネルギーと時間の不確定性関係について
グッドラック さんのレス (2009/02/27(Fri) 17:23)
tohrisugari-sanさん
ありがとうございます.大変勉強になりました.
しかしエネルギーの値に下限がある通常の物理系での時間とエネルギーの不確定性関係については,なにか議論はないですかね?=>皆様
なお摂動論の議論は知ってますので,それ以外であったらお願いします.
置き土産 です
tohrisugari-san さんのレス (2009/03/01(Sun) 11:05)
グッドラック様
ハミルトニアンの固有値が下に有界な場合の時間とエネルギーの不確定性ですが, パウリの定理の存在のため,平均二乗誤差に関する不等式を任意の状態に対して導くことはできません.
しかし状態空間の中の特定の部分空間(正確にはドメイン)に属する量子状態に対して時間演算子を導入して不確定性関係の不等式を出すことは可能です.
例えば自由粒子系のハミルトニアン
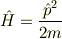
に対して,
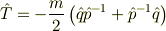
というものを考えます.これは二乗可積分である関数全体がなす状態空間に対しては,演算子として定義されないものです.
しかし,運動量表示の波動関数 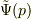 において原点
において原点 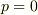 周辺で急激に零なる関数だけを集めて作られる部分空間では演算子として振舞います.
周辺で急激に零なる関数だけを集めて作られる部分空間では演算子として振舞います.
さらにそのエルミート性も成り立ち,
![[\hat{H},\ \hat{T}]=i\hbar](http://hooktail.maxwell.jp/bbslog/9af590d27ee4feb81e7c8eacfa3cce26.png)
も満たすことが証明できます.
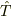 のように,全状態空間内部ではエルミート演算子ではないが部分空間でエルミート演算子として振舞うものは,シンメトリック演算子を呼ばれており,シンメトリックな時間演算子の研究は数学の分野として今でも研究が盛んなようです.
のように,全状態空間内部ではエルミート演算子ではないが部分空間でエルミート演算子として振舞うものは,シンメトリック演算子を呼ばれており,シンメトリックな時間演算子の研究は数学の分野として今でも研究が盛んなようです.
それから何年か前の数理科学(?)という雑誌だったかと思いますが,電通大の長岡先生が量子推定の枠組みで厳密に証明できる時間とエネルギーの不確定性関係の不等式の話をされていたように思います.
これはAという人物がある波動関数を未知の時間間隔  だけ時間発展させて,得られた波動関数をBという人物に渡して測定させて
だけ時間発展させて,得られた波動関数をBという人物に渡して測定させて  の値を推定させるという問題の中で出てきます.
の値を推定させるという問題の中で出てきます.
 の推定誤差
の推定誤差 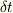 と,与えられた状態でのハミルトニアンの分散値
と,与えられた状態でのハミルトニアンの分散値 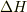 との間に
との間に
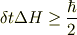
という関係があることを証明できる話だったかと記憶しています.(定かでなくてすみません.)
Re: 置き土産 です
グッドラック さんのレス (2009/03/02(Mon) 04:47)
ありがとうございました.結構あるもんなんですね,この不確定性関係に関する議論.知らない話ばかりで,大変面白かったです.また何かあったら教えてください.