分極ベクトルと分極電荷密度の関係
分極ベクトルと分極電荷密度の関係
gok さんの書込 (2009/02/21(Sat) 18:17)
初めまして.趣味で電磁気学を勉強している高2の学生です. 誘電分極のメカニズムについて質問があります.
分極電荷密度と分極ベクトルの関係式
「分極電荷体積密度を 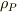 ,分極ベクトルを
,分極ベクトルを 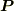 とおくと,
とおくと,

が成り立つ.」
の根拠がよく分かりません.私の持っている教科書(ファインマン物理学など)は全て,以下のように説明しています.
「誘電体内部に適当な領域(体積  ,表面積
,表面積  )をとる.
領域表面に生じた分極電荷は,”領域の表面を通って領域外部に出ていく電荷”とも考えられ,これを
)をとる.
領域表面に生じた分極電荷は,”領域の表面を通って領域外部に出ていく電荷”とも考えられ,これを 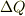 ,分極電荷面密度を
,分極電荷面密度を 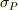 とおくと,
とおくと,
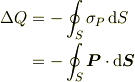
と書ける(↑ここまでは理解できます).一方, 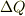 は分極電荷の体積密度
は分極電荷の体積密度 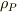 を用いて
を用いて
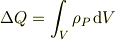
と書くこともできるため(↑この式が理解できません!),
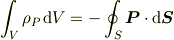
である.その後,右辺にGaussの発散定理を用いて,両辺を微分して……,(以下略)」
ここに出てきた 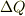 と
と 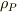 の関係式は,どういう論理の上に成り立っているのでしょうか?
初歩的な質問かも知れませんが,どなたかご教示ください.よろしくお願い致します.
の関係式は,どういう論理の上に成り立っているのでしょうか?
初歩的な質問かも知れませんが,どなたかご教示ください.よろしくお願い致します.
Re: 分極ベクトルと分極電荷密度の関係
mNeji さんのレス (2009/02/21(Sat) 22:57)
gokさん,とても進度が高いですね.
>誘電分極のメカニズムについて質問があります.
と言う事ですが,むしろ「誘電分極のイメージ」が出来ていますか?
今回の問題点は,そのイメージに基づいて積分形で表した数式(面積分と体積分の関係式:ガウスの公式)を用いる事で,(偏)微分形の式で表すというプロセスを如何にして理解するか,だろうと思います.
数学のツールとしては,ベクトル解析の知識が明瞭になっていないと,どうしても表面的な理解に終わってしまう危険性が大きいと思います.
むしろお若いのですから,じっくりと物理数学的な図書を勉強されることをお勧めします.自分は年寄りなので,近年の図書を広く存じませんが,
「理工系の数学入門コース 3,ベクトル解析」, 戸田 盛和・著, 岩波書店, ISBN4-00-007773-2
などをご覧になって見るのも一法だと思います.
Re: 分極ベクトルと分極電荷密度の関係
toorisugari no Hiro さんのレス (2009/02/23(Mon) 13:54)
gokさん,この問題が解けますか?
「点  における金の質量密度が
における金の質量密度が 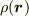 である合金がある.この合金のある領域
である合金がある.この合金のある領域 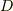 における金の質量を積分を使って表現せよ.」
これが分からないなら,mNejiさんのおっしゃるとおりベクトル解析の教科書を読まれる事をお勧めします.
における金の質量を積分を使って表現せよ.」
これが分からないなら,mNejiさんのおっしゃるとおりベクトル解析の教科書を読まれる事をお勧めします.
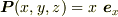 となる分極ベクトル場のイメージは分かりますか?(各分極が格子状に並んでいるとし,また,分極を格子幅だけ離れた二つの電荷で近似して,考えてください.)
となる分極ベクトル場のイメージは分かりますか?(各分極が格子状に並んでいるとし,また,分極を格子幅だけ離れた二つの電荷で近似して,考えてください.)
これが分かれば,  のイメージはある程度つかめると思います.
のイメージはある程度つかめると思います.
Re: 分極ベクトルと分極電荷密度の関係
gok さんのレス (2009/02/23(Mon) 17:47)
mNejiさん,toorisugari no Hiroさん,ご返信ありがとうございます.
今まで物理的なイメージを疎かにしてきたつもりは全くありませんでしたが, どうやら私には,目の前の現象を柔軟に考える訓練が足りないようです.反省.
>金の質量の問題
求める質量は,微小領域(体積 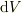 )における金の質量
)における金の質量 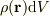 を全て足し合わせることで得られる.つまり
を全て足し合わせることで得られる.つまり
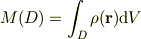
である.…という答で間違いないでしょうか? 積分の基本的な概念どおりに書いたつもりですが,間違っていたら何とも情けないです.
>分極ベクトル場のイメージ
これがいまいち良く分かりません. 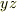 平面に一様なベクトル場で,
平面に一様なベクトル場で, 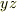 平面から離れるほど大きくなることは読み取れますが,誘電体とどう関係しているのかが分かりません.
恥ずかしい話ですが,分極ベクトルについて理解しているのは,
・単位体積当りの電気双極子モーメントであること
(電気双極子モーメントは,異符号で絶対値の等しい2電荷の大きさと距離から定義される量であること)
・
平面から離れるほど大きくなることは読み取れますが,誘電体とどう関係しているのかが分かりません.
恥ずかしい話ですが,分極ベクトルについて理解しているのは,
・単位体積当りの電気双極子モーメントであること
(電気双極子モーメントは,異符号で絶対値の等しい2電荷の大きさと距離から定義される量であること)
・ 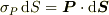 が成り立つこと(自力で証明済)
の2つだけです.
が成り立つこと(自力で証明済)
の2つだけです.
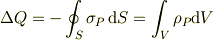
問題となっているこの式についてですが,これを日本語で言うと,
-(領域表面に生じた(表面から出て行った)分極電荷の合計)=(領域全体における分極電荷の合計)
という事になると思われます.が,これがどういう意味なのかが理解できないでいるのです.「表面から出て行った」という言い方もしっくり来ません. 電気双極子が無数に集まっているだけで,表面付近と領域全体は対等であるはずなのに,このような関係式が成立するのはなぜですか?
Re: 分極ベクトルと分極電荷密度の関係
toorisugari no Hiro さんのレス (2009/02/23(Mon) 18:11)
> つまり 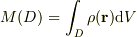 である.…という答で間違いないでしょうか?
である.…という答で間違いないでしょうか?
大丈夫です.あと,ガウスの定理は大丈夫ですか?
> >分極ベクトル場のイメージ > これがいまいち良く分かりません.
一次元で考えましょう. 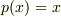 という双極子場があるとします.これは原点から離れる向きにあり,かつ,原点からの距離に比例する強さを持ちます.
という双極子場があるとします.これは原点から離れる向きにあり,かつ,原点からの距離に比例する強さを持ちます.
これを離散近似します.双極子を距離1だけ離れた異符号の電荷の組と考え,また,場は格子だと考えます.このとき,強さ  の双極子を位置
の双極子を位置  に加えることは,点
に加えることは,点 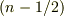 と点
と点 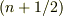 にそれぞれ
にそれぞれ 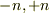 の電荷を加えていくことに等しいです(
の電荷を加えていくことに等しいです( 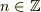 ).
).
![[n_1,n_2]](http://hooktail.maxwell.jp/bbslog/32de38d328baf18aaf43edb76df60bad.png) のすべての格子点
のすべての格子点  に双極子を加えた後,場を観測すると,領域
に双極子を加えた後,場を観測すると,領域 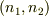 内の各点
内の各点 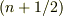 (
( 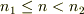 )に「隣り合う双極子で電荷を相殺した残りの電荷」
)に「隣り合う双極子で電荷を相殺した残りの電荷」 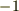 があることになりますね.これは,
があることになりますね.これは, 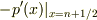 に相当します.その総和は
に相当します.その総和は 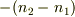 です.
です.
ですが,境界 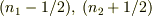 に余分な電荷
に余分な電荷 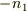 と
と 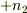 があります.その和を
があります.その和を  としましょう.そもそも双極子は合計すれば電荷0です.ということは領域
としましょう.そもそも双極子は合計すれば電荷0です.ということは領域 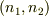 にはその和の反対電荷
にはその和の反対電荷 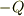 があるはずです.先ほどの総和と一致しますね.
があるはずです.先ほどの総和と一致しますね.
# 間違いがあったので修正しました.
Re: 分極ベクトルと分極電荷密度の関係
gok さんのレス (2009/02/27(Fri) 19:45)
ご返信ありがとうございます.
離散近似というものは初耳ですが(量子力学的手法でしょうか?),大まかには理解できました. 結局は, -(領域から出ていった電荷の合計)=(中に残った電荷の合計) (∵自由電荷が無いと仮定したとき,分極電荷が無ければ領域内の電荷の合計は0) という事だったのですね.
Gaussの発散定理も大丈夫です. (領域全体を1つの湧き出し口として考えたときの湧き出し量)=(領域内部の全ての点における湧き出し量の総和) という感覚で理解しています.
Re: 分極ベクトルと分極電荷密度の関係
toorisugari no Hiro さんのレス (2009/02/27(Fri) 21:14)
> 離散近似というものは初耳ですが(量子力学的手法でしょうか?),
単なる近似です.
(1) 連続な双極子場を格子状に並んだ双極子の集まりで近似します.
(連続な関数 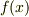 を格子点での値の集まり
を格子点での値の集まり 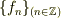 で置き換えて考える事です.(ただし,
で置き換えて考える事です.(ただし, 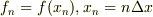 ) )
) )
さらに
(2) 双極子を有限の距離に離れた異符号の電荷の対に置き換える.
(これは微分の差分近似 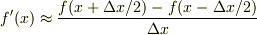 に相当します.)
に相当します.)
という近似操作をつかっただけです.
(人によりますが,)離散的な方がイメージがしやすいかなと思ったわけです.