波動関数の浸みこみ効果について
波動関数の浸みこみ効果について
tohrisugari-san さんの書込 (2009/02/21(Sat) 17:53)
はじめまして.1次元シュレーディンガー方程式のよくある演習問題の解釈で質問があります.質量  の粒子が以下のポテンシャルの中を運動するときの波動関数に関してです.
の粒子が以下のポテンシャルの中を運動するときの波動関数に関してです.
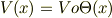
ここで 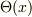 はヘビサイドのステップ関数で,
はヘビサイドのステップ関数で, 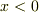 ではポテンシャルは消えていて,
ではポテンシャルは消えていて, 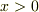 では
では 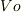 という値をもつポテンシャルとなってます.そして
という値をもつポテンシャルとなってます.そして 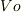 はある正の値とします.この設定でエネルギー
はある正の値とします.この設定でエネルギー  が
が 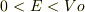 を満たす場合のハミルトニアンの固有関数を求めます.この固有関数はポテンシャル領域の左から粒子がやってきて,ポテンシャル壁に反射するという境界条件で解かれます.この問題自体は教科書などに解説があるので,関数はすぐに解けます.その結果得られる波動(固有)関数について質問です.
を満たす場合のハミルトニアンの固有関数を求めます.この固有関数はポテンシャル領域の左から粒子がやってきて,ポテンシャル壁に反射するという境界条件で解かれます.この問題自体は教科書などに解説があるので,関数はすぐに解けます.その結果得られる波動(固有)関数について質問です.
古典力学とは異なり, 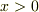 の領域の波動関数は零になりません.指数関数的に小さくなりますが粒子の存在確率があり,ポテンシャル領域への浸みこみ効果があります.従って粒子の位置測定をしたとすると,非零の確率で粒子は
の領域の波動関数は零になりません.指数関数的に小さくなりますが粒子の存在確率があり,ポテンシャル領域への浸みこみ効果があります.従って粒子の位置測定をしたとすると,非零の確率で粒子は 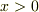 の領域に見い出されます.もし粒子が
の領域に見い出されます.もし粒子が 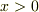 で見つかったとするならば,その粒子のエネルギーは
で見つかったとするならば,その粒子のエネルギーは 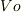 以上のはずです.しかしもともとの波動関数で決まっていた粒子のエネルギーは
以上のはずです.しかしもともとの波動関数で決まっていた粒子のエネルギーは  であり,
であり, 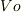 より小さな値です.この結論はエネルギー保存則と矛盾しないのでしょうか?
より小さな値です.この結論はエネルギー保存則と矛盾しないのでしょうか?
Re: 波動関数の浸みこみ効果について
mNeji さんのレス (2009/02/21(Sat) 23:14)
量子力学では,不確定性原理:粒子のエネルギーがそのエネルギーEからの変動幅ΔEにあるとき,その状態いる時間幅Δt;
ΔE*Δt 〜 h
がある為に,
「極短時間のΔtの範囲では,エネルギー保存を破ったエネルギでの測定も在り得る」
と理解したら如何でしょうか?
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/22(Sun) 08:36)
mNejiさん
レスありがとうございます.まず「不確定性原理:粒子のエネルギーがそのエネルギーEからの変動幅ΔEにあるとき,その状態いる時間幅Δt;ΔE*Δt 〜 h」というのがよくわかりません.変動幅とその状態にいる時間幅の定義を解説して頂けると助かります.
これは摂動論で出てくるエネルギー保存則の破れの話でしょうか?
無限時間経ったあとでの遷移確率を摂動で計算するとデルタ関数の形の因子が現れて始状態と終状態のエネルギーは同じになるが,有限時間 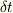 しか経たない遷移確率ではデルタ関数が鈍って,例えばエネルギー幅
しか経たない遷移確率ではデルタ関数が鈍って,例えばエネルギー幅 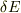 だけ許容する関数になりますよね.その場合だいたい
だけ許容する関数になりますよね.その場合だいたい 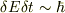 という関係が現れます.もしこの意味での不確定性関係だとすると,今の問題にはあまり関係ないような気もします.摂動論は使っておりませんので.
という関係が現れます.もしこの意味での不確定性関係だとすると,今の問題にはあまり関係ないような気もします.摂動論は使っておりませんので.
それから次のような感じもします.時間に依存しないポテンシャル問題では(測定過程を除いて)波動関数はシュレーディンガー方程式を満たすので,エネルギーは厳密に保存するはずです.したがってエネルギーはどの時刻で測ってもいいはずで,無限に時間の経った後( 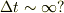 )でエネルギーを測れば
)でエネルギーを測れば 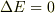 となってしまう気もします.すみませんが,まだよくわかりません.
となってしまう気もします.すみませんが,まだよくわかりません.
Re: 波動関数の浸みこみ効果について
mNeji さんのレス (2009/02/22(Sun) 10:38)
あ,不確定性を持って来るのは可笑しいですね.撤回します,ご免なさい.
今の場合;
左の領域から入射波が進行波として来て,障壁で一部は反転して左に向けて進行波として戻る.残りが右の領域に,減衰波として沁み込む.
と考えて良い訳だと思います.
この場合,全エネルギー,ハミルトニアンの固有値について,障壁の左右で考えると,
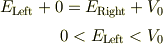
から,右側に沁み込んだ状態では,負の運動エネルギ状態になりますが,全エネルギー保存側は成立していると考えられると思います.
ただ,上記の言い方ではご質問への説明になっていないかも知れません.
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/22(Sun) 12:14)
mNejiさん,ご回答ありがとうございます.いろいろ説明しようとして下さって感謝です.
ただ残念ながらまだ納得できておりません.お返事にあった 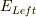 と
と 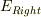 は運動エネルギー
は運動エネルギー
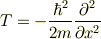
の部分だと思うのですが,この演算子は
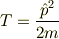
というようにエルミート演算子 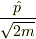 の2乗で書けてます.従ってその固有値も,またなんらかの波動関数での測定値の期待値も負にはならないと思います.もし粒子が
の2乗で書けてます.従ってその固有値も,またなんらかの波動関数での測定値の期待値も負にはならないと思います.もし粒子が 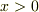 で見つかりましたら,粒子の状態は
で見つかりましたら,粒子の状態は
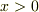 の領域だけ零ではない,ある波動関数
の領域だけ零ではない,ある波動関数 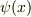 の状態にジャンプすると思うのですが.もしこれが正しければ,例えばその状態での運動エネルギーの期待値
の状態にジャンプすると思うのですが.もしこれが正しければ,例えばその状態での運動エネルギーの期待値
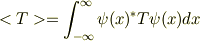
も,ポテンシャルエネルギーの期待値
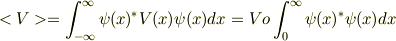
も正になっていると思われます.もし波動関数が規格化されていれば
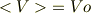
とできるはずなので,測定前のエネルギー 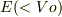 に比べて少なくとも期待値の意味で
に比べて少なくとも期待値の意味で
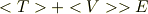
となって,エネルギーが増えているように見えます.このためエネルギー保存則が破れているように見えてしまいます.
Re: 波動関数の浸みこみ効果について
mNeji さんのレス (2009/02/22(Sun) 12:52)
tohrisugari-san,
残念なことに,上手く説明ができないので,私の意見はこれまでとします.識者の方々の助言をお待ち下さい.
Re: 波動関数の浸みこみ効果について
yama さんのレス (2009/02/22(Sun) 15:20)
の領域の波動関数を
の形で表すと
を虚数とすればシュレーディンガー方程式を満たすことができ,エネルギーは保存されます.
しかし, 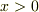 のときに運動量が虚数になるというわけではありません.
粒子の位置を測定して,
のときに運動量が虚数になるというわけではありません.
粒子の位置を測定して, 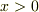 が得られたとしても,そのときは運動量が確定値をとりません.
逆に運動量を測定すれば必ず実数値が得られますが,そのときは粒子の位置が確定しません.
が得られたとしても,そのときは運動量が確定値をとりません.
逆に運動量を測定すれば必ず実数値が得られますが,そのときは粒子の位置が確定しません.
Re: 波動関数の浸みこみ効果について
グッドラック さんのレス (2009/02/22(Sun) 15:58)
単に測定する時,測定器系から粒子の系にエネルギーが流れこんでいるのではないですか?この問題に限らずエネルギーの保存則が破れて見えるときの「常」は,見落としている外部系があって,その系まで含めて全系を考えるとエネルギーは保存するようになるという答えが多いように思います.
Re: 波動関数の浸みこみ効果について
toorisugari no Hiro さんのレス (2009/02/23(Mon) 15:47)
難しい問題ですね.「観測」とは何かがよく分かっていないのが問題じゃないかなと思います.グッドラックさんのおっしゃるとおり外部の影響を考えるべきでしょう.
例えば, 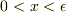 の間に
の間に 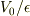 の電場がコンデンサーなどで作られていて,コンデンサーにあいた小さな穴に
の電場がコンデンサーなどで作られていて,コンデンサーにあいた小さな穴に 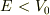 のエネルギーを持つ電荷を入射する装置が,対応するものとして考えられます.
のエネルギーを持つ電荷を入射する装置が,対応するものとして考えられます.
ここで, 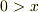 において電子を観測するには乾板等をおくわけですが,「観測」とは,乾板等の分子との反応をみることで行います.つまり,電子にとっては
において電子を観測するには乾板等をおくわけですが,「観測」とは,乾板等の分子との反応をみることで行います.つまり,電子にとっては  より低いポテンシャル領域が
より低いポテンシャル領域が 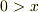 の一部に存在することになります.
の一部に存在することになります.
つまり, 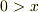 において電子を観測したとき,それはトンネル効果がおきたと解釈されるだけで,エネルギー保存則が破れたわけでも虚数運動量になるわけでもありません.装置に幅を持たせて運動量も観測させたとしても,
において電子を観測したとき,それはトンネル効果がおきたと解釈されるだけで,エネルギー保存則が破れたわけでも虚数運動量になるわけでもありません.装置に幅を持たせて運動量も観測させたとしても,  より低いポテンシャル領域における運動量(+装置の幅に由来する不確定性)が観測されるだけです.
より低いポテンシャル領域における運動量(+装置の幅に由来する不確定性)が観測されるだけです.
当然,乾板をコンデンサーから離すと,観測される確率は減りますが,それは 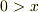 における波動関数から計算される確率と比例するはずです.
における波動関数から計算される確率と比例するはずです.
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/23(Mon) 16:49)
yamaさん,グッドラックさん,toorisugari no Hiroさん,ご回答ありがとうございます.
yamaさんのご説明は,観測を考えない場合にエネルギー固有関数がどのようにシュレーディンガー方程式を満たしているのかをまずご説明頂いて,その後で測定により状態が乱されることの重要性をご指摘されようということですね.ここでいうと
位置演算子 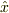 とハミルトニアン
とハミルトニアン 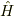 が演算子として非可換なことに対応するのでしょうか?はじめ状態は
が演算子として非可換なことに対応するのでしょうか?はじめ状態は 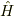 の固有状態にあったわけですが,位置領域の観測により観測後の状態は
の固有状態にあったわけですが,位置領域の観測により観測後の状態は 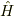 の固有状態ではなくなっているという事実のことならば,そのことは問題提起に取り込み済みだと思われます.問題は観測前後でエネルギー(の期待値)が変化するわけで,その差分はどこから来たかという問題となっております.
の固有状態ではなくなっているという事実のことならば,そのことは問題提起に取り込み済みだと思われます.問題は観測前後でエネルギー(の期待値)が変化するわけで,その差分はどこから来たかという問題となっております.
グッドラックさんのご指摘は大変ポイントを得ているように考えます.もう少し考えさせて頂きます.
toorisugari no Hiroさんのご回答も大変具体的で,問題へのアプローチに道をつけて頂くものかと考えます.ただ確認させて頂きたいのですが,電場のかかっていない領域は 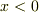 と
と 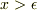 ですよね.それでポテンシャルは
ですよね.それでポテンシャルは
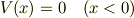
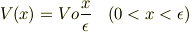
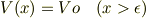
という具合のモデルと理解してよろしいでしょうか?そして粒子はコンデンサ左側からエネルギー 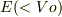 で入射するという設定でよろしいでしょうか?もしそうであれば,浸みこみの量子効果は
で入射するという設定でよろしいでしょうか?もしそうであれば,浸みこみの量子効果は 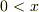 (より正確には
(より正確には 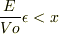 )に起こると思うのですが,ご回答にある
)に起こると思うのですが,ご回答にある 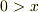 は誤植でしょうか?また追加ですみませんが,観測用の乾板は粒子と反応して時間発展し,その状態を変えて測定結果を知らせる機能が必要だと思います.この観測過程は,乾板から来る新たな局所的ポテンシャルを入射粒子のシュレーディンガー方程式に加えるだけで,記述は十分なのでしょうか.
は誤植でしょうか?また追加ですみませんが,観測用の乾板は粒子と反応して時間発展し,その状態を変えて測定結果を知らせる機能が必要だと思います.この観測過程は,乾板から来る新たな局所的ポテンシャルを入射粒子のシュレーディンガー方程式に加えるだけで,記述は十分なのでしょうか.
Re: 波動関数の浸みこみ効果について
toorisugari no Hiro さんのレス (2009/02/23(Mon) 17:35)
> ご回答にある 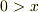 は誤植でしょうか?
は誤植でしょうか?
ですね.
> 観測用の乾板は粒子と反応して時間発展し,その状態を変えて測定結果を知らせる機能が必要だと思います.この観測過程は,乾板から来る新たな局所的ポテンシャルを入射粒子のシュレーディンガー方程式に加えるだけで,記述は十分なのでしょうか.
いいえ.何らかの多段階過程が必要でしょう.ですが,浸みこみで粒子が観測されるという「矛盾」を除去するには,  より小さい(有効)ポテンシャルがあることだけ考えれば十分なのでは?
より小さい(有効)ポテンシャルがあることだけ考えれば十分なのでは?
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/23(Mon) 17:55)
toorisugari no Hiro様
ご回答ありがとうございます.「浸みこみで粒子が観測されるには,より小さい(有効)ポテンシャルがあることだけで十分なのでは?」ということですが,これはよくわかりません.
つまりこれでは最初からポテンシャルに窪みのあるものを採用してトンネリングのあるポテンシャル問題を解いているのと質的に変わらない気がします.
トンネリングを考えても,トンネルを十分する時間発展をさせた後で十分な精度で位置を測れば,測定後の状態は空間座標  の関数としてデルタ関数的に局在した状態になることでしょう.
の関数としてデルタ関数的に局在した状態になることでしょう.
そのフーリエ変換で得られる運動量分布から評価される測定後のエネルギー期待値は,もともとのエネルギー  よりも高い
よりも高い 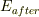 という値になるはずです.
という値になるはずです.
この 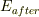 のオーダーを定めるのはもともとのトンネリングのポテンシャルではなく,位置測定の機器のパラメータが決めるのではないでしょうか?
のオーダーを定めるのはもともとのトンネリングのポテンシャルではなく,位置測定の機器のパラメータが決めるのではないでしょうか?
また「装置に幅を持たせて運動量も観測させたとしても,より低いポテンシャル領域における運動量(+装置の幅に由来する不確定性)が観測されるだけです.」というコメントもよく理解できません.もう少し解説して頂けますでしょうか?
Re: 波動関数の浸みこみ効果について
toorisugari no Hiro さんのレス (2009/02/23(Mon) 18:17)
> つまりこれでは最初からポテンシャルに窪みのあるものを採用してトンネリングのあるポテンシャル問題を解いているのと質的に変わらない気がします.
私は「観測する」とはそういうことだと理解しています.
> この |959d368efef672cda342d118554f644d| のオーダーを定めるのはもともとのトンネリングのポテンシャルではなく,位置測定の機器のパラメータが決めるのではないでしょうか?
それのどこが問題なのか理解しかねます.
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/23(Mon) 18:35)
toorisugari no Hiro様
ご回答ありがとうございます.
「私は「観測する」とはそういうことだと理解しています.」
観測するという行為は,注目している粒子の系と計測器にあたるプローブ系との相互作用によって粒子の情報が計測器に移って,その情報に関して乾板上の化学反応のように「信号増幅」の過程が続いて,その結果現れる情報が刻まれたマクロな対象(測定器の針の位置などの)を古典的な意味で測定をするものではないでしょうか?
この後半部分はtoorisugari no Hiro様のご回答にもあった「何らかの多段階過程が必要でしょう.」というコメントにも対応する部分かと推測します.
すると測定装置と注目粒子は相互作用を通じてエネルギーをやりとりしても不思議には思えません.従って注目粒子の系だけで観測前後のエネルギー値が保存するという設定は決して一般的な状況を説明していないように思えます.
toorisugari no Hiro様のご説明でも,乾板と粒子の間の相互作用がなけれはなにも意味のある観測できないと思います.この不可欠な測定の相互作用のために,グッドラックさんのご指摘にもありましたが,やはり粒子と測定器の合成系で全エネルギーが保存されていると思うのが自然に思えるようになりました.
「それのどこが問題なのか理解しかねます.」ということですが,測定に関してすごく微調整された特殊な場合を議論されているように感じております.
頂いた回答が一般の場合にも通じる説明だとすると,乾板と粒子の相互作用がなぜ合成系の全エネルギーだけではなく個々の部分系のエネルギーも測定の相互作用の前後で保存するのかをtoorisugari no Hiro様に説明して頂ければ,こちらは納得できるかもしれません.
Re: 波動関数の浸みこみ効果について
toorisugari no Hiro さんのレス (2009/02/23(Mon) 18:41)
> すると測定装置と注目粒子は相互作用を通じてエネルギーをやりとりしても不思議には思えません.
それを有効ポテンシャルと表現したつもりですが.
もちろん,厳密には,粘性現象と同じようにポテンシャルは存在せず,外部とのカップリングを考え,全体のエネルギー保存を考えるべきでしょう.
でも,染み込み領域で虚数の運動量が出ることに対する矛盾の解消は,有効ポテンシャルを考えるだけで十分では?
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/23(Mon) 19:00)
toorisugari no Hiro様
「それを有効ポテンシャルと表現したつもりですが.」ということですが,トンネリングを出されて説明されていましたので,静的なポテンシャル項 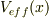 をもとのポテンシャル
をもとのポテンシャル 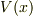 に加えて窪みをつけられたとの理解をしておりました.つまり
に加えて窪みをつけられたとの理解をしておりました.つまり
![i\hbar\frac{\partial}{\partial t}\Psi(x,t)\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)+V_{eff}(x) \right]\Psi(x,t)](http://hooktail.maxwell.jp/bbslog/688c48f9a3fe1468bbcc854876a1e42e.png)
を考えることが観測することだと主張されているように読めました.違いましたか?もしこの意味だと 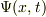 は粒子だけを記述する波動関数です.測定器の自由度は入っておりません.このシュレーディンガー方程式ではもちろんエネルギーは保存しますが,これは粒子だけのエネルギーですよね.また乾板と粒子の相互作用がなぜ
は粒子だけを記述する波動関数です.測定器の自由度は入っておりません.このシュレーディンガー方程式ではもちろんエネルギーは保存しますが,これは粒子だけのエネルギーですよね.また乾板と粒子の相互作用がなぜ 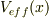 という形だけで記述できるものに限定できるのかが理解できていない状況です.
という形だけで記述できるものに限定できるのかが理解できていない状況です.
一般には測定器の変数を 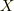 として,全体系の波動関数
として,全体系の波動関数 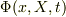 が
が
![i\hbar\frac{\partial}{\partial t}\Phi(x,X,t)=\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)+U_{eff}(x,X)+H_{detector} \right]\Phi(x,X,t)](http://hooktail.maxwell.jp/bbslog/575af36364fd4af2ebafac72d3987b0a.png)
というシュレーディンガー方程式を満たすのではないでしょうか?ここで 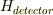 は測定器の自由ハミルトニアンです.
は測定器の自由ハミルトニアンです.
有効ポテンシャル 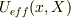 がなぜtoorisugari no Hiro様の場合のように
がなぜtoorisugari no Hiro様の場合のように 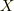 を含まない
を含まない 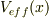 のように書けるのかを説明して頂ければ,納得できるのではないかと思われます.
のように書けるのかを説明して頂ければ,納得できるのではないかと思われます.
そうすれば,全エネルギーだけでなく,粒子のエネルギーだけでも保存する理由ができるようになります.よろしくお願いします.
Re: 波動関数の浸みこみ効果について
toorisugari no Hiro さんのレス (2009/02/23(Mon) 19:07)
「有効」ですから,最後の式を 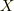 のすべての状態で平均したものと考えていただいて結構です.
のすべての状態で平均したものと考えていただいて結構です.
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/23(Mon) 19:13)
「「有効」ですから,最後の式を 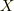 のすべての状態で平均したものと考えていただいて結構です.」
のすべての状態で平均したものと考えていただいて結構です.」
では質問の仕方を変えさせて頂きます.
粒子の系と測定器系の合成系において,測定の相互作用において測定器の一部のエネルギーは粒子に移るのが一般的とお考えでしょうか?
それとも粒子の系はあくまで,自分の中だけでエネルギー収支をつけて保存させているとお考えでしょうか?
お答え頂けるとtoorisugari no Hiro様のご回答の真意がわかるかと思います.
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/23(Mon) 19:19)
よく考えると「「有効」ですから,最後の式を 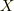 のすべての状態で平均したものと考えていただいて結構です.」ということの正当性,根拠もよくわかりません.ご説明頂けたら幸いです.
のすべての状態で平均したものと考えていただいて結構です.」ということの正当性,根拠もよくわかりません.ご説明頂けたら幸いです.
Re: 波動関数の浸みこみ効果について
toorisugari no Hiro さんのレス (2009/02/23(Mon) 19:31)
> 粒子の系と測定器系の合成系において,測定の相互作用において測定器の一部のエネルギーは粒子に移るのが一般的とお考えでしょうか?
「有効ポテンシャル」が厳密にポテンシャルとしての意味を持つなら,自分の中だけでエネルギー収支をつけて保存させるでしょう.ですが,一般には,外部とのエネルギー収支があると思います.相互作用があるときに厳密なポテンシャルが存在するか否かは私には分かりません(たぶん否定的でしょうが).
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/23(Mon) 20:27)
toorisugari no Hiro様
「「有効」ですから,最後の式を 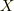 のすべての状態で平均したものと考えていただいて結構です.」「どう疑問をもたれているのでしょうか? 」
のすべての状態で平均したものと考えていただいて結構です.」「どう疑問をもたれているのでしょうか? 」
例えば,なぜすべての状態で平均化するのでしょうか?これは測定器系の状態すべてを平均化するということをおっしゃっているのですよね?
結局有効ポテンシャルの定義としてどのようなものを採用されて,このようなコメントを付けられたのか想像できないのが原因です.
その定義を明確にして頂いて,それに基づいて先のコメントの正当性,根拠をご説明頂ければ,幸いです.
Re: 波動関数の浸みこみ効果について
toorisugari no Hiro さんのレス (2009/02/23(Mon) 20:39)
> これは測定器系の状態すべてを平均化するということをおっしゃっているのですよね?
そうです.
> なぜすべての状態で平均化するのでしょうか?
観測装置を表に見せないためです.(私は熱浴をイメージしています).
![\mathrm{i}\hbar\frac{\partial}{\partial t}\Phi(x,X,t)&=\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)+U_{int}(x,X)+H_{detector} \right]\Phi(x,X,t)](http://hooktail.maxwell.jp/bbslog/a7a048fab1776dfff546431b2c17579f.png)
を平均して
![\left \langle \left[U_{int}(x,X)+H_{detector} \right]\Phi(x,X,t) \right \rangle_X = V_{eff}(x) \left \langle \Phi(x,X,t) \right \rangle_X](http://hooktail.maxwell.jp/bbslog/ec8daa4702f78ecb0d2eb405a5dc1337.png)
で 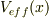 を定義しています.もちろん,
を定義しています.もちろん, 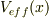 が存在する保証はありません.
が存在する保証はありません.
Re: 波動関数の浸みこみ効果について
yama さんのレス (2009/02/23(Mon) 23:51)
位置の測定によってエネルギーが変化するのは当然であって,その原因としては既に提案されているように,測定装置との相互作用が考えられるでしょうね. ところで,エネルギー保存則というのは,エネルギーの期待値が時間的に変化しないこと,特に定常状態ではどんな時刻に測定しても同じ値が得られることを意味していると思いますが,位置の測定によって変化しないということは意味していないと思います. 従って,位置の測定によってエネルギーが変化することが,エネルギー保存則に矛盾することにはならないと思います.
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/24(Tue) 06:49)
toorisugari no Hiro様
「状態のすべてを平均化」の定義をもっと精密にコメントして頂かなければ,コメント自体が私だけでなく他の方にも理解できなくなると思います.
ご回答頂けるのありがたいですが,handwavingな議論ではなく今はもっと緻密な議論をして頂ける方にコメントしてもらえればと願っております.
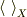 の定義をきちんと書いて頂けないでしょうか?
の定義をきちんと書いて頂けないでしょうか?
また熱浴をイメージされているそうですが,そうすると「すべての状態で平均化する」というご説明から連想されるものと異なる感じがします.まるで高温極限で,あらゆる状態を同じ重みで平均化すると読めておりました.
それから波動関数を集団平均(?)された 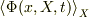 は物理的に意味がないかと思います.平均化操作において規格化条件をどのように保たれるのでしょうか?
は物理的に意味がないかと思います.平均化操作において規格化条件をどのように保たれるのでしょうか?
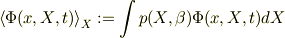
のような類では,規格化条件は平均操作後で満たされません.(ここで 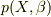 は
は 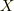 の確率分布密度関数で,
の確率分布密度関数で, 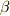 は自然単位系においての温度の逆数です.)従って物理的に意味のある確率解釈もできないかと思います.
は自然単位系においての温度の逆数です.)従って物理的に意味のある確率解釈もできないかと思います.
yama様
論理を整理されてコメントして頂ければ幸いです.
量子力学では,交換しない2つのエルミート演算子に対応する物理量A,Bがあるとき,Aの期待値などがBの測定の後で変化するというのは,いわば原理的なレベルで正しい主張です.これについて疑問を呈しているわけではありません.
量子力学で認められている物理量の測定による撹乱過程は実際に起こるのですから,そのとき「エネルギー保存則は実際どのようになっているのか?」というのが,問題なのです.
ですから「エネルギー保存則に矛盾することにはならないと思います.」という部分において,``では実際にどのように矛盾していないのかを明らかにしてください.”ということなのです.
yama様のコメントにはまだこのことに関しての内容が含まれておりませんので,よく理解できないという状況なのです.
Re: 波動関数の浸みこみ効果について
ASA さんのレス (2009/02/24(Tue) 08:53)
はじめましてtohrisugari-sanさん. 極自然な疑問ですね. ここで緻密な議論を期待しても無理で,量子測定理論関連のペーパーを当るしかないと思います.量子測定系をどうモデル化すれば現象とうまく対応できるかは難しい問題です. >従って粒子の位置測定をしたとすると,非零の確率で粒子はの領域に見い出されます. どのような装置なり方法で位置測定をするかというのが,ポイントだと思います.これをきっちり定義させれば,議論が進むかもしれません.
>もし粒子がで見つかったとするならば,その粒子のエネルギーはV0以上のはずです. 問題の前提はエネルギーの固有状態でしょうか? なら,測定系によっては,エネルギー保存の要請から,測定系に反応しないとも考えられますね. 確かに,波動関数の単純な確率解釈が,あらゆる測定系について汎用的であるか疑問がありますよね.
Re: 波動関数の浸みこみ効果について
yama さんのレス (2009/02/24(Tue) 09:35)
エネルギー保存則は,外部との相互作用がある場合にもエネルギーが保存するということではないので,測定装置との相互作用によってエネルギーが変化してもエネルギー保存則には矛盾しないということです. このことは古典力学でも同様であって,当然のことだと思います. ただし,古典力学では測定の際の相互作用を原理的にはいくらでも小さくできるのに対して,量子力学ではそれが不可能であるということが大きな違いでしょうね.
Re: 波動関数の浸みこみ効果について
tohrisugari-san さんのレス (2009/02/24(Tue) 13:04)
ASA様
「ここで緻密な議論を期待しても無理で,」に関しては,疑問符です.
toorisugari no Hiroさんを初め,こちらでコメント頂いた方々は十分物理をご存じで,素養をお持ちであると感じております.
またここは公開掲示板でもあるために特定の方々のみがコメントをつけるだけでなく,ASA様のような方も現れてコメントしてくださる機会があり得るわけです.
そういう意味でこちらの掲示板には大きな可能性があり,レポート問題やゼミの準備のための家庭教師的存在を超えて,高いレベルまでカバーされた物理議論の場になり得るかと感じております.
「どのような装置なり方法で位置測定をするかというのが,ポイントだと思います.」とは例えばどのようなことを明らかにしながら議論をすることなのでしょうか.具体的な例をお挙げ頂ければ,参考になるかと思います.お時間のあるときにでも,書き込みして頂ければ有難く思います.
「問題の前提はエネルギーの固有状態でしょうか?なら,測定系によっては,エネルギー保存の要請から,測定系に反応しないとも考えられますね.」において,エネルギーの固有状態であることがどのくらい今の議論で本質的なのでしょうか.
測定器系とのエネルギーのやり取りを認めると,特に粒子系だけのエネルギー保存則はないように思えます.コメントは例えば次のような意味なのでしょうか.一般的な測定器ではなく,ある特定の測定器では粒子系の中で測定前後でもエネルギーを保存させる場合があり得て,その場合にはその装置で決して位置測定を実現できない可能性のことでしょうか.
「確かに,波動関数の単純な確率解釈が,あらゆる測定系について汎用的であるか疑問がありますよね. 」に関しては,全く同感であります.
yama様
コメントありがとうございます.おっしゃりたいことをまとめさせて頂くと,グッドラックさんのコメントと同様の内容かと思われます.
粒子系だけではエネルギーは保存しないが,粒子系+測定器系の全エネルギーは保存するという考え方ということでよろしいでしょうか.
Re: 波動関数の浸みこみ効果について
yama さんのレス (2009/02/25(Wed) 00:39)
エネルギーの保存という場合は,普通は粒子系だけについてのことだと思います. つまり,粒子系が定常状態にあれば,系のエネルギーは測定をしない限り一定に保たれ,いつ測定しても同じ値が得られるということです. 測定を何回繰り返しても同一の値が得られるということではありません.
Re: 波動関数の浸みこみ効果について
mNeji さんのレス (2009/02/26(Thu) 11:19)
量子力学も落ちこぼれた私ですが,どうもこれまでの論議に納得がいきません.
とくに「新たなポテンシャルを導入」すると言った方向には戸惑いを感じています.
ヒョットすると,最近の半導体技術をもちいた「疑似孤立量子系」のような実験などを基にした研究などが進んでいるのかも知れませんが,そこらの分野はどうなのでしょうか?
で,元の話にもどりますが,この問題は;
ある空間に自由運動エネルギKで運動している粒子が,その空間よりも外にポテンシャルの大きさVがKより大きい,V>K場合,どのように理解するか?
と思います.
もう少し,状況を広げて,普通のポテンシャル散乱のように
ある空間にポテンシャルVinの基に運動エネルギKinで運動している粒子が,その空間よりも外にポテンシャル障壁の大きさV >(Kin + Vin)で,領域が幅Lに存在して,その外側には,ポテンシャルがなくなり自由運動をする場合,これをどのように理解するか?
といった場合はどうなのでしょうか?
このような場合,ポテンシャル障壁をトンネル現象として透過してくる振る舞いから,内部構造についての知見を得るのではないでしょうか?
半導体工学のなかで,似た様な現象をどう取り扱っているのでしょうか?
Re: 波動関数の浸みこみ効果について
ASA さんのレス (2009/02/26(Thu) 12:30)
>>高いレベルまでカバーされた物理議論の場になり得るかと感じております. 参加メンバーによりけりですが,まず専門家は参加しないので過剰な期待は無駄かと.
>>具体的な例
理想測定を前提とするか否か等.理想測定を前提にするなら,yamaさん意見の大部分は,除外できるかと.(そもそも,一般の位置測定で粒子のエネルギーの推定はできても,確定するわけでないから問題といえるのか?) また,測定器等については,上にに挙げられた文献リストが取り掛かりになるのでないかと.
>エネルギーの固有状態であることがどのくらい今の議論で本質的 確定値でなければ,話にならないかと.
確かにtoorisugari no Hiroさんの >染み込み領域で虚数の運動量が出ることに対する矛盾の解消は,有効ポテンシャルを考えるだけで十分では? は,無理筋でしょう(事実,困惑されている方もおられますし).
オーソドックスな解釈では,何が矛盾となりどう解決されているか知りませんが,個人的には量子ポテンシャルによる解釈で問題視しません.
ボーム流のエネルギーは,E=T+V+Q:Q;量子ポテンシャル 障壁内では実関数なので,T=0,V=V0,Q=E0-V0 フリーでは平面波で,T=E0,V=0,Q=0 系のエネルギーはE0で変りません.
オーソドックスなエネルギーは,E=p^2/2m+V.これも,系のエネルギーはE0で変りませんね. 測定器によりけりでしょうが,虚数の運動量,即ち,負のエネルギーですから,系が測定器からエネルギーを奪うことに対応するようにも思えますね.
なんにせよ,位置観測と同時に系のエネルギーを取り出す測定器なら,エネルギー保存則により制限され観測されないとなるでしょうね.
Re: 波動関数の浸みこみ効果について
てんふー さんのレス (2009/02/26(Thu) 13:37)
> tohrisugari-san - 2009/02/22(Sun) 12:14 No.23009 のレスとして:
そもそも,時間無依存のSchrodinger方程式の導出過程に立ち戻れば,エネルギー  とは,系の全エネルギー演算子
とは,系の全エネルギー演算子 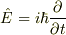 の期待値です.全エネルギー
の期待値です.全エネルギー 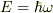 に対する時間無依存の波動関数
に対する時間無依存の波動関数 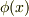 から,時間依存の波動関数
から,時間依存の波動関数 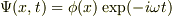 を求めて期待値を計算すれば,
を求めて期待値を計算すれば, 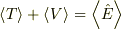 が成立します.
が成立します.
観測問題でもありません.また,統計力学(多粒子系)の「熱浴」を持ち出すのも,おかしいです.
Re: 波動関数の浸みこみ効果について
naruheso さんのレス (2009/02/26(Thu) 13:58)
これはtohrisugari-sanさん,大変ですね〜...
回答群を大別すると次の2つのグループに分けられるのかな?
(1)測定自体全く眼中にない.ポテンシャル障壁があるハミルトニアンの固有値問題を解くことにのみ関連するコメント.確かに 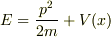 からシュレーディンガー方程式
からシュレーディンガー方程式
![Eu(x)=\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} +V(x)\right]u(x)](http://hooktail.maxwell.jp/bbslog/7f3aa58b27ac6eb32b84cad9715c8579.png)
は作られたけど,この方程式を 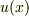 が満たすからといって,それをエネルギー保存則とは言わないでしょう.やっぱり.ハミルトニアンに対するハイゼンベルグ演算子の時間微分が消えるとか,エネルギー測定の時の確率分布関数が時間変化しないとかが,所謂「エネルギー保存則」でしょ.外部の系との接触がなければね.これらに対する対応は,測定器系という外部系がちゃんと別個あって,粒子系はそれとちゃんと相互作用をして,エネルギーもヤリトリするというのを強調するしかないかな.
が満たすからといって,それをエネルギー保存則とは言わないでしょう.やっぱり.ハミルトニアンに対するハイゼンベルグ演算子の時間微分が消えるとか,エネルギー測定の時の確率分布関数が時間変化しないとかが,所謂「エネルギー保存則」でしょ.外部の系との接触がなければね.これらに対する対応は,測定器系という外部系がちゃんと別個あって,粒子系はそれとちゃんと相互作用をして,エネルギーもヤリトリするというのを強調するしかないかな.
(2)外部の測定器系との相互作用を考えているケース.これは一歩前進のケースですね.ここで粒子系と測定器系の合成系をどのように記述するかに,意見の相違があるように見える.
(1)のグループの人は,tohrisugari-sanの2009/02/22(Sun) No.23009 のコメントをよく読んでから再出発したほうがいいかも...
Re: 波動関数の浸みこみ効果について
てんふー さんのレス (2009/02/26(Thu) 16:22)
> tohrisugari-san - 2009/02/21(Sat) 17:53 No.22996 の最初の問題に戻ります.
運動エネルギーの値は,古典論では非負ですが,量子論では負もとりえます.
最初の問題で与えられたポテンシャル分布 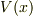 において,単一障壁の障壁内部 = 右側 (
において,単一障壁の障壁内部 = 右側 ( 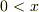 )は,その状況です.実際に計算してみます.
障壁の左側では,粒子は,平面波
)は,その状況です.実際に計算してみます.
障壁の左側では,粒子は,平面波 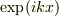 で表されるので(ただし波数
で表されるので(ただし波数  は
は 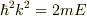 を満たす正数),障壁のすぐ左側の位置
を満たす正数),障壁のすぐ左側の位置 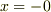 における運動エネルギーは
における運動エネルギーは 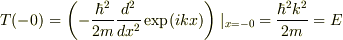 です.
です.
障壁の右側では,粒子は,減衰波 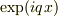 で表されるので(ただし波数
で表されるので(ただし波数  は
は 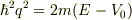 を満たす「純虚数」),障壁のすぐ右側の位置
を満たす「純虚数」),障壁のすぐ右側の位置 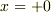 における運動エネルギーは,
における運動エネルギーは, 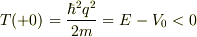 です.
です.
よって, 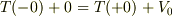 となり,運動エネルギーとポテンシャルエネルギーの和は,障壁の左右で連続します.これが,最初の問題の「エネルギー保存則」でしょう.
となり,運動エネルギーとポテンシャルエネルギーの和は,障壁の左右で連続します.これが,最初の問題の「エネルギー保存則」でしょう.
物理は,エネルギー原点の取り方によらず成立すべきです.もしポテンシャル分布 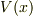 を,障壁の左側で
を,障壁の左側で 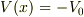 ,右側で
,右側で 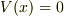 にとると,
にとると, 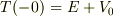 ,
, 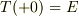 ですから,
ですから, 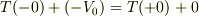 となり,上の意味の「エネルギー保存則」が成立します.
となり,上の意味の「エネルギー保存則」が成立します.
Re: 波動関数の浸みこみ効果について
toorisugari no Hiro さんのレス (2009/02/26(Thu) 16:31)
えっと,私は2のグループにはいるのかな?
外部との結合を考えつつ,縮約あるいは平均操作をすることで,観測結果とエネルギー保存則を両立する単一系のeffectiveな方程式を作れないかと思いましたが,ハミルトニアンの非エルミート性,あるいは波動関数のノルム非保存を無視できるからくりが分からないので,挫折です.
観測装置をうまく選ばないと,観測が物理的だったり,非物理的だったりするのが変ですね.ということで,2は抜けるかもしれません.
でも,よく考えると,そもそもの問題の前提が正しいのかが分からなくなってきました.つまり,
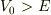 となる領域(古典的禁止領域)で本当に「粒子は観測される」のでしょうか?
となる領域(古典的禁止領域)で本当に「粒子は観測される」のでしょうか?
トンネル効果の実験結果は多いですが,「古典的禁止領域」を破壊せずに(明示的なエネルギー注入やポテンシャルの変形なしに)古典的禁止領域で粒子が観測された事を示す実験結果やデバイスはあるのでしょうか?粒子は運動量と運動エネルギーが実数値を取る状態だと理解してますが,本当に「粒子」は古典的禁止領域で観測されるのでしょうか?
私が無知なだけで,既にみなさんがご存じならごめんなさい.
量子測定とエネルギー保存則
tohrisugari-san さんのレス (2009/02/26(Thu) 19:38)
皆様
多くのご回答ありがとうございます.
ただいろいろな誤解が多岐に渡り存在しており,その1つ1つを解いていくのも,その数の多さの故,大変なことだというのが実感です.
ただグッドラックさんのご指摘で自分の中で問題を再整理するきっかけを得ることができました.
そこで私が問いたい問題を,余分な混乱を切り捨てられるモデルで,再提案させて頂くことが一番いいのではないかと思います.
それに基づいて再考して頂いて,コメントを頂けましたらと思います.
問題の核心はあくまで「量子測定」となっています.
問題:1次元調和振動子を考えます.そのハミルトニアンは
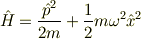
で与えられています.
このハミルトニアンの最低固有値状態 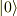 は基底状態とも呼ばれます.(ここで規格化は済んでいるとします.)
は基底状態とも呼ばれます.(ここで規格化は済んでいるとします.)
その固有値は 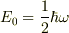 という正の値であるということはよく知られ,零点振動のエネルギーとして理解されています.
という正の値であるということはよく知られ,零点振動のエネルギーとして理解されています.
この定義により 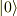 は最低エネルギー状態です.あらゆる意味で,この状態より小さなエネルギーをとる量子状態はありません.
は最低エネルギー状態です.あらゆる意味で,この状態より小さなエネルギーをとる量子状態はありません.
つまりエネルギー固有値としても 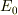 は最低であり,またあらゆる量子状態でのエネルギー期待値ももちろん
は最低であり,またあらゆる量子状態でのエネルギー期待値ももちろん 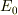 を下回ることはありません.
を下回ることはありません.
この調和振動子が 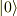 の状態にあるとします.
の状態にあるとします.
ここで任意のエルミート演算子で記述される物理量 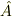 を考えます.そして
を考えます.そして 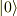 の状態において,この
の状態において,この 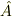 を理想測定しましょう.
を理想測定しましょう.
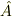 の固有値問題は解けているとし,その固有値を
の固有値問題は解けているとし,その固有値を 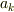 と書き,対応する規格化された固有状態を
と書き,対応する規格化された固有状態を 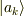 と書くこととします.
と書くこととします.
理想測定を行うとボルンの公式から 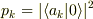 の確率で
の確率で 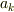 という測定結果が出現することがわかります.
という測定結果が出現することがわかります.
理想測定ですので, 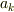 という結果が観測された後の状態は
という結果が観測された後の状態は 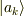 に変化していることになります.
に変化していることになります.
ここで測定後の調和振動子のエネルギーが平均していくらになったかを評価してみましょう. それは
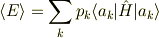
で計算されます.
このとき定理として次のことが示せます.
定理: 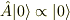 とはならない
とはならない 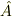 に対して
に対して
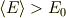
という関係がなりたつ.ここで等号が成り立たないのがポイントです.
この証明は後ですることにして,ここで私が提起してきた問題をこのモデルで再提案いたします.
測定前にエネルギーは(期待値の意味でも) 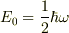 でした.
でした.
測定後にエネルギーは 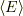 になってしまいました.
になってしまいました.
このエネルギー差
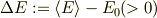
は,どこから来たのでしょうか?
この問に関して,皆様のご意見から考えられる可能性は以下のものでしょうか.
可能性(1)エネルギーが増えることは,エネルギー保存則に反するので,基底状態に対する 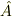 の理想測定は実現できない.
の理想測定は実現できない.
可能性(2)理想測定を行う装置から調和振動子にエネルギー 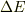 が流れ込んで,励起させている.
が流れ込んで,励起させている.
他にもあるかもしれませんが,ご意見を頂ければと思います.
このモデルの利点はトンネリングや,波動関数がどのようにシュレディンガー方程式を満たすかなどの混乱原因を避けられることです.
残されていた定理の証明ですが,簡単です.
まず基底状態の定義から,任意の状態 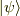 に対して
に対して
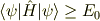
が言えます.この不等式の等号は 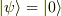 が成り立つ時だけ成立します.それ以外では成り立ちません.各固有値
が成り立つ時だけ成立します.それ以外では成り立ちません.各固有値  に対しても
に対しても
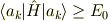
が成り立ちます.この両辺に 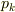 をかけて
をかけて  に関する和をとると
に関する和をとると
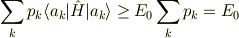
となり,
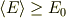
が得られます.
ここでポイントは,次の点です.
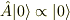 とならないため,必ず
とならないため,必ず 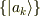 には基底状態とは異なる状態が含まれます.従って
ある
には基底状態とは異なる状態が含まれます.従って
ある 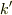 が存在して
が存在して
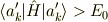
となっていることがキーです.
従って先ほどの不等式の等号は決して成り立たないので,
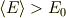
が証明されました.
Re: 量子測定とエネルギー保存則
ASA さんのレス (2009/02/26(Thu) 20:58)
tohrisugari-sanさん このように整理された形の問題なら理解しやすいですね. AとHが同時固有値を持つか否かで違ってくるような気がしますが, 可能性(1)可能性(2)共にあって測定する物理量と測定器に依存すると考えます.(そもそも,理想測定が不可能ということはさておいて)
>基底状態とは異なる状態が含まれます. 基底状態を破壊する観測が行われるならそうでしょう.
Aの観測より破壊された状態で,後に実行されるエネルギー観測によって,<E>>E0が得られるわけですが,このときにエネルギーがやりとりされる可能性も考えられますね.
Re: 量子測定とエネルギー保存則
yama さんのレス (2009/02/26(Thu) 23:11)
量子力学における時間発展にはシュレーディンガー方程式に従う変化と,観測による状態の変化(いわゆる波束の収縮)の2通りあって,エネルギーの保存則は前者について成り立つのだと思います. 後者については,ハミルトニアンと交換しない物理量を測定した場合にエネルギーが変化することもあると思いますが,それは測定装置との相互作用によるものでしょう.つまり可能性(2)が成り立つと思います.
というのは単純すぎる考え方でしょうか?
Re: 量子測定とエネルギー保存則
tohrisugari-san さんのレス (2009/02/27(Fri) 04:59)
議論が収束する方向ができたようで,ひと山越えた感じですね.
一般の場合には可能性(2)がもっともらしいと感じ,ある特別な観測量の選択と特別に調整された実験装置を使う場合だけ可能性(1)もあり得るというスタンスが主流をなすのではないでしょうか.
そうでないと感じる方がいらっしゃいましたら,コメントして頂ければと思います.
可能性(2)の考え方は,量子力学の深い側面を教えてくれている気がします.
基底状態と言えどもいろいろな物理量の観測を行うと,調和振動子がその状態で"持っている"様々な個性のある情報を教えてくれます.
しかし"持っている"とは言え,この振動子の物理特性が世に関わりを持てるのは,測定器や他の系からエネルギーをもらったときだけではないでしょうか?
つまり可能性(2)を信じると,物理的属性の顕現は外部の測定器系のエネルギー注入があってこそ,実現しているということになります.
もし測定器が十分なエネルギーを持っていなければ,基底状態は多様な性質を表しません.
これはある意味,「測定装置(のエネルギー)が調和振動子の物理属性をこの世に実現させている」とも言えそうです.
振動子の波動関数はいわば「設計図」であり,エネルギーが系に入ってくれば その設計図に則っていろいろな物理的属性を実際に創出し,設計図どおりの確率分布を与える...ようにも見えてしまって,とても深く,とても興味深いです.
ASA様
コメントありがとうございます.細かいところですが,
「(そもそも,理想測定が不可能ということはさておいて)」
の部分に関してコメントです.もちろん理想測定は実験する場合には極限でしか実現しないと思います.
ただ,限りなく理想測定に近い実験は可能です.たとえば有名な電子スピンを測定するシュテルンとゲルラッハの実験なんか理想測定に近いものと言えます.
スピンの2準位状態の情報を,不均一な磁場との相互作用によって電子の空間的位置の情報に焼きなおしています.
時間を十分かければ,スピンアップ状態の電子の位置と,ダウン状態の電子の位置の間の距離はマクロにいくらでも大きくなり,電子の位置の確認により精度のいいスピン測定が可能になります.
yama様
「というのは単純すぎる考え方でしょうか? 」という部分について,そうは思いません.
ただもっと議論を具体化すると,きちんとした確証が得られるのではないでしょうか.
なにかアイデアがありましたら,またコメントを頂ければと思います.
波動関数は測定結果の「設計図」に過ぎないか
tohrisugari-san さんのレス (2009/02/27(Fri) 10:25)
調和振動子モデルで問題認識を共有できたようなので,再び元のポテンシャル浸みこみNo.22996に戻ろうかと思います.
メッセージを込めて,タイトルを変えさせて頂きました.
前コメントにおいて,波動関数(状態ベクトル)は「設計図」のようなものと書かせて頂きましたが,このことはこのポテンシャル問題でより興味深い響きが出るように思います.
最初に与えられている粒子のエネルギー  は,ポテンシャル障壁
は,ポテンシャル障壁 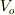 より小さく設定されておりました.
より小さく設定されておりました.
しかしそのポテンシャル障壁領域にも波動関数は浸みこんでいて,粒子の非ゼロの存在確率を示しています.
位置測定の後,もし粒子がそのポテンシャル領域に見つかったならば,測定後の状態はそこに局在する規格化された波動関数 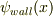 で記述されます.
で記述されます.
そしてその測定後粒子のエネルギーは,
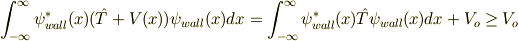
という関係が必ず満たされることから,確かに 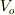 より小さくはないということが保証されています.
より小さくはないということが保証されています.
調和振動子のモデルでの知見から,このエネルギーの増分は位置測定の機器から流入したものと解釈されます.
準備の説明が終わったので,「波動関数は測定結果の設計図」という意味を説明することができます.
測定後の状態 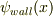 にある粒子はポテンシャル内部に居ることのできる十分なエネルギーを持っていて,その後運動を起こすことができる「実粒子(real particle)」とも呼べるものです.
にある粒子はポテンシャル内部に居ることのできる十分なエネルギーを持っていて,その後運動を起こすことができる「実粒子(real particle)」とも呼べるものです.
一方測定前に波動関数の浸みこみでしか表現できなかった,ポテンシャル領域に”存在”していた粒子は,言わば「仮想粒子(virtual particle)」という類と思えます.つまりそこに「存在する」というには十分なエネルギーを持たないからです.
もし位置測定を行ったとすると,ある確率でポテンシャル領域に実粒子が現れる,というのが波動関数の予言するところです.
例えて言うならば,測定過程はビル工事のようなものです.
工事(測定)をする前には手元にはビルの設計図(波動関数)しかありませんが,工事(測定)の日には建築業者(測定機器)によって必要な資材(エネルギー)が運ばれてきて,設計図を見ながらビル(実粒子の顕在化)を建てるわけです.
つまり,工事(測定)の前にはビル(実粒子)は,存在していないのです.
このことから,測定そのものがポテンシャル領域に粒子を作り上げているというのは言い過ぎでしょうか?
量子力学における測定の謎めいた役割には興味が広がります....
Re: 波動関数は測定結果の「設計図」に過ぎないか
mNeji さんのレス (2009/02/27(Fri) 11:02)
tohrisugari-sanさん,
興味深く論議を拝見しています.論議とは少し離れた提案をお伝えします.
この掲示版は,一つのスレッドが長くなると,見通しが悪く成りがちです.
まして,複数の論議が並行的に進むと,混乱しがちです.これまでのタイトルだけでも,
・波動関数の浸みこみ効果について ・量子測定とエネルギー保存則 ・波動関数は測定結果の「設計図」に過ぎないか
と変遷してきました.それぞれに,方向を変えた問題意識が示されて来たとおもいます.
とくに「量子測定」はすでに論議済みと思われますが,私に取っては,むしろ「量子測定」は「粒子の位置測定」に限定する方法しか無いのかが疑問です.
そういう意味では,対象モデルの量子力学的な構築と平衡して,例えば電磁場との相互作用をモデル化することも入れて置かないと,論議が噛み合ない様に感じます.
何れにしろ,活発な論議を楽しみにしています.
Re: 波動関数は測定結果の「設計図」に過ぎないか
tohrisugari-san さんのレス (2009/02/27(Fri) 12:53)
mNeji様
コメントありがとうございます.
「この掲示版は,一つのスレッドが長くなると,見通しが悪く成りがちです.」というご指摘ですが,ごもっともだと思います.これはタイトルを変えて話題転換するときには,別スレッドにすべきということでしょうか.以後はそのように配慮させて頂きます.
「とくに「量子測定」はすでに論議済みと思われますが,」とありますが,「済み」とは思っておりません.いろいろご意見をお聞かせ頂ければと思います.
「私に取っては,むしろ「量子測定」は「粒子の位置測定」に限定する方法しか無いのかが疑問です.」:この文章は,「位置以外の物理量の測定も議論すべき」というご指摘なのか,それとも他の意図で書かれたことなのでしょうか.もし前者ならば同意見でして,もっと多様な観測量の測定を皆様と論じていければと願っております.
「そういう意味では,対象モデルの量子力学的な構築と平衡して,例えば電磁場との相互作用をモデル化することも入れて置かないと,論議が噛み合ない様に感じます.」 これも同じ意見ですが,なかなかそこまでたどり着いていないのが現状です.その方向に議論を誘導して頂ければ,こちらもドンドン乗っていきたいと思います.
ご提案の方向性は,ちょうど測定過程のモデル構築の議論にもなるかと思います.
Re: 波動関数は測定結果の「設計図」に過ぎないか
mNeji さんのレス (2009/02/28(Sat) 00:25)
tohrisugari-sanさん,
>「私に取っては,むしろ「量子測定」は「粒子の位置測定」に限定する方法しか無いのかが疑問です.」:この文章は,「位置以外の物理量の測定も議論すべき」というご指摘なのか,それとも他の意図で書かれたことなのでしょうか.もし前者ならば同意見でして,もっと多様な観測量の測定を皆様と論じていければと願っております.
誤解の無い様に,先に申し上げますが,私は量子力学の落ちこぼれです.正統的な理解力はありません.感触に基づいた当てずっぽうをお許し下さい.
さて,上記の意見が出て来た裏側を先に述べますと,「調和振動子モデル」を拝見した時に思い浮かべたのは「プランクの量子仮説」にでてきた調和振動子モデルです.当時,これを見たとき,原子や分子の運動の量子化しか頭の中に無かった私は,一時大混乱しました.
今から見れば,電磁波の量子化では,次の特徴があります; ・電磁波の固有エネルギ値が直接の観測量になっている ・電磁波自体が熱源との相互作用を組み込んでいる
他方,水素原子の量子化では; ・水素原子核と軌道電子とから生みだされる固有エネルギ値は必ずしも,直接されない. ・ただし,電荷を持つ為に,電磁波との相互作用は自動的にモデルに内包されている.
そこで,お書きになった「調和振動子モデル」にも,外系との相互作用を明示的に取り込む必要性があるのではないかと考えました.
また,固有エネルギ値に付いてですが,水素原子の例を考えても,基底状態の固有エネルギ値は,原理的にも直接量として観測可能です.例えば,質量分析計で精密測定出来ると思います.所が,励起状態のエネルギ値は,直接観測されていません.そうです,輝線スペクトルは,固有エネルギ準位間のエネルギ差を持ち出した電磁波のエネルギ値の観測,言い換えれば間接的観測量であります.
その類推からすると「調和振動子モデル」で得られた固有エネルギのセットを計算しただけで,その「量子測定」が解明されるのだろうか,そもそも完全孤立系では,純粋固有状態間の遷移が生じないのではないかと,思った次第です.
以上,漠然とした話で済みません.
スレッドをわけます
tohrisugari-san さんのレス (2009/02/28(Sat) 08:43)
mNeji様からのご提案により,以下に関するスレッドを分けたいと思います.すみませんが,これらに関するコメント頂ける場合には新しいスレッドにお願いいたします.
・量子測定とエネルギー保存則 ・波動関数は測定結果の「設計図」に過ぎないか
Re: 波動関数は測定結果の「設計図」に過ぎないか
ASA さんのレス (2009/02/28(Sat) 08:46)
tohrisugari-sanさん >限りなく理想測定に近い実験は可能です.たとえば有名な電子スピンを測定するシュテルンとゲルラッハの実験なんか理想測定に近いものと言えます. そりゃ,エネルギーと同時固有値をもつようなスピン測定なら,問題は少ないですよ.その場合は,観測されるエネルギーはE0で変らないので,<E>>E0の定理が成立しない. 問題なのは,運動量測定のような場合で,ご存知のように運動量固有状態は,平面波なので,位置x→∞でもnon0.x→∞で0になる束縛状態とは様子が全く違う.測定でポテンシャルを破壊すると考えるか.もしくは,ポテンシャルがそのままなら,平面波の<V>は発散してるので,測定器が無限大のエネルギーを与えないといけなくなる.どちらの考えにせよ,現実離れしているように思えます. このようなことから,量子測定関連の議論は,安易に物理量Aと一般化できないように感じてます.何をどのように測定するかを明確にしないといけないかと.
mNejiさん >完全孤立系では,純粋固有状態間の遷移が生じないのではないかと 被測定糸と測定系をmixした量子系を考えるべきということでしょうか? どっかでselection(収縮)を適用するのだから,どこかで境界ができますよ. いきなり複雑なモデルにすると,わけが判らなくなるような気がします.
あと,単一水素原子モデルで電磁波ありを考えても,特定エネルギーの電磁波しか関係しませんよね.関係する電磁波があると,定常状態でなくていわゆる重ね合わせ状態なので,特定の電磁波を吸い取った状態,もしくは,吐き出している状態が観測されるわけです.