半円筒転がり振子

Yokkun さんの書込 (2009/02/16(Mon) 22:33)

中身の詰まった半円筒形の水平面上での転がり振動を解析しています．手近にあったガラス製半円プリズムで実験したところ0.53sec. 理論値0.66sec. との差が気になっています．摩擦なしで滑る場合は理論値0.54sec.なのですが，滑っている様子もありません．どこか勘違いまたは，計算違いをしているのだろうと思っています．よろしければ，ご検討ください．

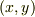半円筒の半径を，質量をとします．傾き角 $\theta$ のときの重心の座標 (x,y) および重心の速度 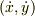$(\dot{x},\dot{y})$ は，

$x=R\left(\theta-\frac{4}{3\pi}\sin\theta\right)\qquad,\qquad\dot{x}=R\dot{\theta}\left(1-\frac{4}{3\pi}\cos\theta\right)$ $y=R\left(1-\frac{4}{3\pi}\cos\theta\right)\qquad,\qquad\dot{y}=R\dot{\theta}\cdot\frac{4}{3\pi}\sin\theta$

なお，半円の重心は円中心から 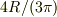$4R/(3\pi)$ の距離にあることを用いました．

一方，重心まわりの慣性モーメントは平行軸の定理により，

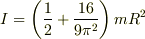
$I=\left(\frac{1}{2}+\frac{16}{9\pi^2}\right)mR^2$

ただし，円筒の慣性モーメント 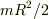mR^2/2 を用いました．

初期条件を 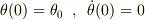$\theta(0)=\theta_0\,\,\,,\,\,\,\dot{\theta}(0)=0$ とすると，エネルギー保存により

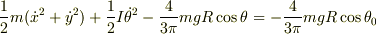$\frac{1}{2}m(\dot{x}^2+\dot{y}^2)+\frac{1}{2}I\dot{\theta}^2-\frac{4}{3\pi}mgR\cos\theta=-\frac{4}{3\pi}mgR\cos\theta_0$ すなわち， $\frac{1}{2}mR^2\dot{\theta}^2\left(\frac{3}{2}+\frac{32}{9\pi^2}-\frac{8}{3\pi}\cos\theta\right)=\frac{4}{3\pi}mgR(\cos\theta-\cos\theta_0)$

周期を求めると，

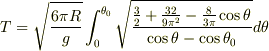
$T=\sqrt{\frac{6\pi R}{g}}\int_0^{\theta_0}\sqrt{\frac{\frac{3}{2}+\frac{32}{9\pi^2}-\frac{8}{3\pi}\cos\theta}{\cos\theta-\cos\theta_0}}d\theta$

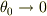となり， $\theta_0\rightarrow 0$ の極限で，ガラスプリズムの値|d41d8cd98f00b204e9800998ecf8427e|R=0.045|d41d8cd98f00b204e9800998ecf8427e|を代入すると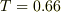， T=0.66 sec.となりました．

一方，摩擦なしの場合は 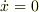$\dot{x}=0$ だから，

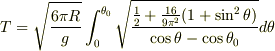
$T=\sqrt{\frac{6\pi R}{g}}\int_0^{\theta_0}\sqrt{\frac{\frac{1}{2}+\frac{16}{9\pi^2}(1+\sin^2\theta)}{\cos\theta-\cos\theta_0}}d\theta$

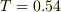となり，理論値は T=0.54 sec.となりました．

ガラスプリズムでの測定値は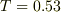， T=0.53 sec.でした．もちろん，見たところ滑りはなく，きれいな転がり振動をしているように見えます．

以上，考察の過程でおかしいところがありましたらご指摘いただけると幸いです．

Re: 半円筒転がり振子

mNeji さんのレス (2009/02/17(Tue) 00:42)

良く判らないのですが，

＞摩擦なしの場合は $\dot{x}=0$ だから，

というのはどうしてですか？

Re: 半円筒転がり振子

Yokkun さんのレス (2009/02/17(Tue) 08:43)

mNejiさん，早速のレスありがとうございます．話題にのっていただいただけでも感謝です．

＞摩擦なしの場合は 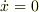$\dot{x}=0$ だから，というのはどうしてですか？

説明不足ですみません．半円筒を置く水平面方向（半円筒断面方向）をx方向としたのですが，初期条件 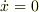$\dot{x}=0$ から振動させるので，面に平行な力がなければ 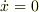$\dot{x}=0$ が保たれて重心は水平方向には動かない，ということでした．

Re: 半円筒転がり振子

mNeji さんのレス (2009/02/17(Tue) 10:58)

＞重心は水平方向には動かない

とすると，重心は垂直方向には動く訳ですね．

その上，何処かの軸について回転するには，どんな運動が生じているのか見えません．

〜〜〜〜〜と書きましたが〜〜〜〜〜

<pre> A O B ********・******** * G * * ・ * * * * * ________________*_*_______________水平面

</pre>

静かに置いた時に上記の様な名称をつけるとして，Gは水平方向に動けないので，Oが水平方向に移動しながら，Gは半球を水平面に接しながら上昇するのでしょうか？

もしそうならば，ABの振動と，Oの純粋な水平振動，Gの純粋な垂直振動が観察されるかもしれません．

Re: 半円筒転がり振子

yama さんのレス (2009/02/17(Tue) 11:20)

重心まわりの慣性モーメントの式が正しくないように思います．

$I=\left(\frac{1}{2}-\frac{16}{9\pi^2}\right)mR^2$

になるのではないでしょうか．

Re: 半円筒転がり振子

Yokkun さんのレス (2009/02/17(Tue) 12:24)

yamaさん，ありがとうございます！！

円筒を半分にしないままの平行軸の定理を使っちゃったんですね！平行軸の定理が重心を基準にしていることをすっかり忘れてました．＾＾；さっそく訂正して数値計算したところ，ぴったり0.53sec. 実験の通りになりました．本当に助かりました．

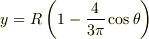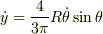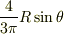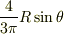mNejiさん，関心をもっていただいてありがとうございます．重心は， $y=R\left(1-\frac{4}{3\pi}\cos\theta\right)$ にしたがって，θの振動とともに上下振動します．傾き角θのときの瞬間の回転中心は， $\dot{y}=\frac{4}{3\pi}R\dot{\theta}\sin\theta$ からもわかるように，重心の高さで重心から $\frac{4}{3\pi}R\sin\theta$ だけはなれたところになります．Ｏ点もこの瞬間中心のまわりに回転をするわけですね．Ｏ点のx座標は， $\frac{4}{3\pi}R\sin\theta$ で瞬間中心の真上になりますから，Ｏ点の速度は常に水平になるのですね！高さが変わらないのだからあたりまえですが．やはり，こうしていろいろ論議・提示していただくと，大変勉強になります．

Re: 半円筒転がり振子

mNeji さんのレス (2009/02/17(Tue) 14:50)

細かな話ですが(笑い)，

＞Ｏ点のx座標は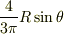，＞ $\frac{4}{3\pi}R\sin\theta$ ＞で瞬間中心の真上になりますから，

瞬間中心というのは「半円が水平面と接触する点(線)」の事だとおもいます．そうすると，O点は常にこの点の垂線上にあるようです．

Re: 半円筒転がり振子

Yokkun さんのレス (2009/02/17(Tue) 20:13)

>瞬間中心というのは「半円が水平面と接触する点(線)」の事だとおもいます．

私は，剛体全体がある瞬間にその点を含む軸のまわりに回転している，という意味で「瞬間中心」といっています．その意味では「半円が水平面と接触する点(線)」はすべりのない転がり運動のときの瞬間中心ですよね？摩擦のないすべり振動のときは，この瞬間中心は接地点真上の重心と同じ高さの点を含む軸になると思います．この軸から重心に引いた水平な線分を半径として重心は鉛直方向に運動しています．

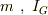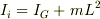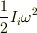ちなみに，瞬間中心軸と平行な重心軸までの距離をとすると，質量および重心軸まわりの慣性モーメントが $m\,\,,\,\,I_G$ である剛体の瞬間の慣性モーメントは，平行軸の定理により， I_i=I_G+mL^2 となり，角速度 $\omega$ での回転を含む運動をしている剛体の全運動エネルギーが $\frac{1}{2}I_i\omega^2$ と書けることになります．瞬間中心軸まわりの回転が，その瞬間における剛体の運動の全てですから，当然ですよね．このことに早く気づいていれば，私のミスもすぐに見つけられたのかもしれませんが，あとの祭りというわけです．