Heisenberg方程式
Heisenberg方程式
snow さんの書込 (2009/02/09(Mon) 23:02)
Schrodinger描像で見たときに,時間tに陽に依存している演算子 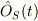 があったとすると,Heisenberg描像に移ったときに,対応する演算子
があったとすると,Heisenberg描像に移ったときに,対応する演算子 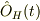 の満たすHeisenberg方程式を求める問題なのですが,
の満たすHeisenberg方程式を求める問題なのですが,
![\frac{d}{dt} \hat{O}_{H}(t)= \frac{1}{i\hbar} [ \hat{O}_{H}(t),\hat{H}] + exp\left(-\frac{1}{i\hbar} \hat{H}(t-t_{0}) \right)\left(\frac{d}{dt} \hat{O}_{S}(t)\right)exp\left(\frac{1}{i\hbar} \hat{H}(t-t_{0}) \right)](http://hooktail.maxwell.jp/bbslog/f5f01fe5480f790c0ce287a9b84efa3c.png) まではわかったのですが,「上式の第2項は,
まではわかったのですが,「上式の第2項は, 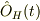 が陽な時間依存を与えているので
が陽な時間依存を与えているので 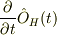 と書ける」と書いていたのですが良く理解できませんでした.
どうしていきなり偏微分になるのでしょうか?
どなたか,お願いします.
と書ける」と書いていたのですが良く理解できませんでした.
どうしていきなり偏微分になるのでしょうか?
どなたか,お願いします.
Re: Heisenberg方程式
toorisugari no Hiro さんのレス (2009/02/10(Tue) 15:34)
Schrodinger描像で位置演算子や運動量演算子は時間に依存しますか?
Re: Heisenberg方程式
snow さんのレス (2009/02/10(Tue) 16:09)
Schrodinger描像では演算子は時間に依存しません. 時間に依存するのは波動関数です.
Re: Heisenberg方程式
toorisugari no Hiro さんのレス (2009/02/10(Tue) 17:35)
>> Schrodinger描像で位置演算子や運動量演算子は時間に依存しますか? > Schrodinger描像では演算子は時間に依存しません.
これら演算子に関しては時間依存性はありません.つまり,演算子は陽には時間に依存しません. 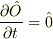
しかし,例えば,回転している装置で位置を測定した場合は,当然,陽に時間に依存します. 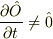
そういうことを言っているのでは?
Re: Heisenberg方程式
snow さんのレス (2009/02/10(Tue) 18:09)
偏微分で記述するのはどうしてですか?
演算子が陽に時間に依存しない場合 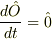 では?
では?
Re: Heisenberg方程式
snow さんのレス (2009/02/10(Tue) 22:00)
えーと,関数が直接  で表されている場合,
陽に
で表されている場合,
陽に  に依存しているというのではないでしょうか?
に依存しているというのではないでしょうか?
Re: Heisenberg方程式
toorisugari no Hiro さんのレス (2009/02/10(Tue) 22:44)
> えーと,関数が直接  で表されている場合,陽に
で表されている場合,陽に  に依存しているというのではないでしょうか?
に依存しているというのではないでしょうか?
たしかに, 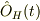 という表現は誤解を生みやすいですね.(かと言って代案はないですが.)
という表現は誤解を生みやすいですね.(かと言って代案はないですが.)
観測量の時間依存というとき,二つの時間の流れがあります.一つはその系の運動によるもの,そしてもう一つはその系の運動によらないもの.後者は観測装置が動く場合や時間に依存する外力が作用する場合等が考えられます.
つまり,
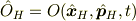
という,位置・運動量演算子を介した陰的なものと陽に記述されたものという,2種類の時間依存性があると言うことです.
Re: Heisenberg方程式
MXK さんのレス (2009/02/11(Wed) 00:30)
たしかに紛らわしいですが,
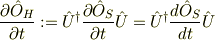
という暗黙の定義,あるいは記法の拡張がなされているということでしょう. 古典の式に合わせるためですね.
別のやりかたとして,まず
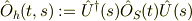
とおいて, 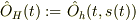 ,
, 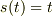
![\frac{d}{d t}\hat O_H(t)=\frac{\partial\hat O_h}{\partial t}+\frac{\partial O_h}{\partial s}\frac{d s}{d t}=\frac{\partial\hat O_H}{\partial t}+\left.(i\hbar)^{-1}\hat U^\dagger(s)[\hat O_S(t),\hat H]\hat U(s)\right|_{s=t}](http://hooktail.maxwell.jp/bbslog/3f34bdd8dbe0fb371f4628e964db4837.png)
この場合でも, 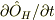 は定義されていると考えないと仕方がないです.
は定義されていると考えないと仕方がないです.
Re: Heisenberg方程式
toorisugari no Hiro さんのレス (2009/02/11(Wed) 13:28)
MXKさんfollowありがとうございます.
古典力学の
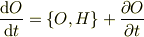
に合わせるように
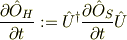
と定義する,つまり,シュレディンガー描像における陽的な時間依存性でハイゼンベルグ描像における時間依存性を定義する,と考えるのが自然ですね.
Re: Heisenberg方程式
snow さんのレス (2009/02/11(Wed) 18:57)
あの,古典の式
 って何のことですか?
って何のことですか?
Re: Heisenberg方程式
MXK さんのレス (2009/02/11(Wed) 23:14)
説明不足で申し訳ありません. 詳しくは解析力学の本を見てもらえばよいと思うので,要点だけ書きます.
古典力学において物理量 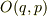 は座標
は座標  と
運動量
と
運動量 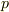 の関数として表せます.
例えば,粒子のエネルギーは
の関数として表せます.
例えば,粒子のエネルギーは 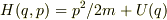 といった具合にです.
ポテンシャルが
といった具合にです.
ポテンシャルが 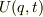 のように時間的に変化する場合まで考慮すると,
物理量を
のように時間的に変化する場合まで考慮すると,
物理量を 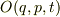 のように時間の関数になるように拡張しておく
必要があります.
物理量の時間変化は,運動方程式
のように時間の関数になるように拡張しておく
必要があります.
物理量の時間変化は,運動方程式 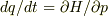 ,
, 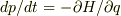 を利用して,
を利用して,
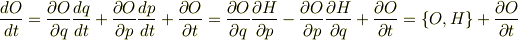
となります.
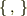 はポアソンの括弧式と呼ばれるもので,直前の式のように
定義されます.
ハイゼンベルク描像はこのように古典論との類似性があるので,好んで使われるのです.
はポアソンの括弧式と呼ばれるもので,直前の式のように
定義されます.
ハイゼンベルク描像はこのように古典論との類似性があるので,好んで使われるのです.