曲率テンソル

曲率テンソル

ファイル さんの書込 (2009/02/08(Sun) 19:21)

リーマン曲率テンソルのところの話です． 教科書に，「完全に等方な場合には，テンソルPは明らかに計量テンソルγだけで表されるはずである．それゆえ，Pの対称性から，それはλを定数として 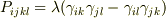P_{ijkl}=\lambda(\gamma_{ik}\gamma_{jl}-\gamma_{il}\gamma_{jk}) という形でなければならない．」という記述があったのですが，なぜそう言えるのかが分かりません． 添え字は1から3までで，三次元の曲率テンソルと三次元の計量テンソルです．

曲率テンソルは，計量と計量一階微分，計量二回微分で表されると思いますが，なぜ等方なときは計量と定数だけになるのでしょうか？ 例えば，三次元計量 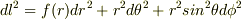dl^{2}=f(r)dr^{2}+r^{2}d\theta^{2}+r^{2}sin^{2}\theta d\phi^{2} は等方的な計量だと思いますが，この一階微分や二階微分には，rやθが残ると思うんです．