振り子の減衰について

振り子の減衰について

K さんの書込 (2009/02/04(Wed) 19:43)

速度に比例する空気抵抗を受けながら運動する振り子についてです．

もし空気抵抗を考慮しないのであれば，振り子の周期は一定であると考えられます．しかし実際，振り子は空気抵抗により減衰するので，振幅角θは時間tとともに小さくなっていきます． 単振り子のようにθが充分小さい時は，たとえθが変わっても周期Tはほとんど変わることはありませんが，一般的に普通の振り子だと，周期Tはθに依存します．

そのため時間tとともに周期Tは小さくなると考えるのですが，定量的な考察がわかりません．どなたか教えていただきたいです．

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/04(Wed) 20:02)

これは何かの課題ですか? 非線形のシステムは考察が難しいです．

第0近似として減衰単振動を考えるのは簡単ですが，振幅が少し大きくなったときの第1近似を求めるには結構タフな摂動計算が必要になります．(多重尺度法)

あるいは，減衰が小さいなら，周期平均では運動エネルギーと位置エネルギーが等分配されると「仮定」して，エネルギーの(周期平均した)時間変化を計算する方法が比較的簡単ですが，どれだけ正しいのか分かりません． # たぶん，この「仮定」自体，振幅が小さいときしか成り立たないでしょうし．

数値計算で行った方が早いと思います．

Re: 振り子の減衰について

K さんのレス (2009/02/04(Wed) 21:54)

長さlのひもに質量mのおもりを取り付け，鉛直方向から角度θの位置から振り子運動させた場合，おもりの運動方向について

運動方程式; ml*(d^2θ/dt^2)=-mgsinθ+kv（k;任意定数）

がなりたつと考えられますが，これよりθをtの関数として求めることができますか？

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/05(Thu) 12:01)

> θをtの関数として求めることができますか？

無理です，たぶん．少なくとも私は聞いたことはありません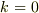． # k=0 なら，楕円関数で記述できますが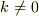， k\ne 0 のとき，楕円関数と指数関数の初等的な組み合わせで 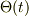\Theta(t) を記述できるとは思えません．

Re: 振り子の減衰について

mNeji さんのレス (2009/02/05(Thu) 15:27)

横から失礼します．

＞長さlのひもに質量mのおもりを取り付け，鉛直方向から角度θの位置から振り子運動させた場合，おもりの運動方向について ＞運動方程式; ml*(d^2θ/dt^2)=-mgsinθ+kv（k;任意定数）

と言う事ですが，「+kv」と，速度に比例した加速を生じる様に思います．スレッド冒頭の

＞速度に比例する空気抵抗を受けながら運動する振り子

と矛盾しませんか．

今，角度θが小さくて，sinθ〜θと近似出来る場合でしたら，運動方程式は，v=ldθ/dtに注意すると， <pre> ml*(d^2θ/dt^2) = -mgsinθ-kv = -mgθ -kldθ/dt </pre>となり，θは，時間についての2次の線形同次微分方程式に従いますね．これを解くのは如何でしょうか？

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/05(Thu) 16:06)

> 矛盾しませんか．

たしかに．まあ，typoでしょう．

> 時間についての2次の線形同次微分方程式に従いますね．これを解くのは如何でしょうか？

これを解くのは簡単ですが，

>> 時間tとともに周期Tは小さくなると考えるのですが，定量的な考察がわかりません

の答えにはなりませんね．

# もっとも，スレ主さんがこのあたりの計算を既に経験されている雰囲気はないので，まずはここから，と言うことなら同意します．

Re: 振り子の減衰について

mNeji さんのレス (2009/02/05(Thu) 22:55)

＞これを解くのは簡単ですが， ＞>> 時間tとともに周期Tは小さくなると考えるのですが，定量的な考察がわかりません ＞の答えにはなりませんね．

私には「上記の疑問：時間tとともに周期Tは小さくなる」自体がそう簡単に判りません．

＞# もっとも，スレ主さんがこのあたりの計算を既に経験されている雰囲気はないので，まずはここから，と言うことなら同意します．

そうですね．あまりに複雑な計算を初めてしまう前に，条件がキツいかもしれないが解析的に求められる解を見てから，非線形な方程式にトライした方が善い様な気がします．

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/06(Fri) 00:03)

> 私には「上記の疑問：時間tとともに周期Tは小さくなる」自体がそう簡単に判りません．

振幅（＝最大角度)が大きくなると単振り子の周期は単振動のそれからズレて長くなります．それは，復元力が線形な場合と較べて小さくなるからです．とくに，最大角度が \pi になると，振り子が上死点で静止してしまうので，周期は無限大になってしまいます． # 定量的な説明はランダウリフシッツ「力学」§11をみてください．

減衰があるときは，有限の振幅から始まるので周期が減衰単振動の周期より長く，振幅が減衰するにつれ，減衰単振動の周期に近づいていきます．

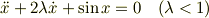
\ddot x +2\lambda \dot x + \sin x &= 0 \quad(\lambda < 1)

に対して，おおざっぱな摂動法で，周期は

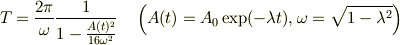
T &= \frac{2\pi}{\omega}\frac{1}{1-\frac{A(t)^2}{16\omega^2}} \quad \left(A(t)= A_0\exp(-\lambda t), \omega=\sqrt{1-\lambda^2}\right)

と評価できます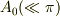． A_0(\ll \pi) は初期振幅です． (「おおざっぱ」といっても相当長いから，計算過程は勘弁．)

Re: 振り子の減衰について

K さんのレス (2009/02/06(Fri) 10:38)

上記の微分方程式は，減衰する振り子についてのものですよね？ 導き方を教えていただきたいです．また「摂動法」とはなんでしょうか．

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/06(Fri) 12:21)

> 導き方を教えていただきたいです．

ここに載せるには，量が多いので勘弁してください．結構高度な計算なので説明しても分かってもらえないと思います．

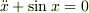\ddot x + \sin x = 0 を摂動法で解くとは，式に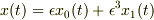 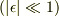x(t)=\epsilon x_0(t) + \epsilon^3 x_1(t) (|\epsilon|\ll 1) を代入して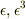， \epsilon, \epsilon^3 の各項がそれぞれ0として線形方程式を導き，解を求める方法です．

ですが，この素朴な摂動法では周期の変化を考慮に入れてないので正しい計算ができません．それを，取り入れた方法が多重尺度法ですが，説明は勘弁してください．

# Kさんが上の素朴な摂動法で 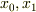x_0,x_1 が導けたなら，多重尺度法を説明します．

まずは，先に示したURLの記事で勉強してください．

Re: 振り子の減衰について

K さんのレス (2009/02/06(Fri) 12:50)

>まずは，先に示したURLの記事で勉強してください．

わかりました．摂動法については勉強することにします．

なんども大変恐縮ですが， d^2x/dt^2+2λx+sinx=0 この方程式そのものは，どのようにして立てられたのですか． 運動方程式に空気抵抗（速度に比例する）を考慮して，整理するとsinθの前に係数ω^2が出てくると思うのですが，どうでしょうか．またλの意味も解りません．

初歩的な質問で申し訳ありませんが，教えてください．

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/06(Fri) 13:02)

ううむ．結構道は遠いみたいですね．

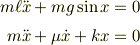
m\ell \ddot x + m g \sin x &= 0\\m \ddot x + \mu \dot x + k x &= 0

それぞれの式において，式を等価に保ったまま，できるだけパラメータを減らしてください．(過程もよろしく)

Re: 振り子の減衰について

K さんのレス (2009/02/06(Fri) 13:58)

前者：空気抵抗なしの振り子の方程式 後者：空気抵抗を考慮した単振動の方程式（バネ定数k,比例定数μ）

と思われますが，なぜこれらをまとめると空気抵抗を考慮した振り子の運動が記述できるのでしょうか．

パラメータもうまい具合に減らして，前述の微分方程式を得ることができません．お手数ですがご教授ください．

Re: 振り子の減衰について

K さんのレス (2009/02/06(Fri) 15:01)

>定量的な説明はランダウリフシッツ「力学」§11をみてください．

今，手元にその本がありません．また，それは上級者向けのものと聞きました．私には理解が困難なのではと思います．どうか，この場を使って説明していただけないでしょうか．頼れる人がいないのです．

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/06(Fri) 15:56)

> パラメータもうまい具合に減らして，前述の微分方程式を得ることができません．お手数ですがご教授ください．

やれるところまではやってください．式全体を定数で割るなどやれることはあるはずです．これが，できないと，空気抵抗を考慮した振り子の運動の記述に進めません．

> この場を使って説明していただけないでしょうか．

とりあえず，宿題が済んでからですね．

Re: 振り子の減衰について

K さんのレス (2009/02/06(Fri) 16:19)

第１式を両辺mlで割ります． (d^2x/dt^2)=-(g/l)sinx これを第２式に代入します． -(mg/l)sinx+μ(dx/dt)+kx=0

・・・さあ，解りません．前述の式に近づきません．どうしたらいいのでしょう．

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/06(Fri) 17:08)

> 前述の式に近づきません．

あ，二つの方程式は別の問題です．それぞれ，テーマがあるんですが，まずは最初の奴を考えましょうか．

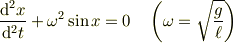
\frac{\mathrm{d}^2 x}{\mathrm{d}^2 t} + \omega^2 \sin x = 0 \quad\left(\omega=\sqrt{\frac{g}{\ell}}\right)

が得られましたね．

ここで，新しい時間変数 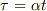\tau = \alpha t ( \alpha 正定数)を導入します． そうすると，

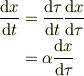
\frac{\mathrm{d} x}{\mathrm{d} t} &= \frac{\mathrm{d} \tau}{\mathrm{d} t}\frac{\mathrm{d} x}{\mathrm{d} \tau}\\&= \alpha\frac{\mathrm{d} x}{\mathrm{d} \tau}

という関係式が得られます．2階微分に関しても同様の関係式が得られます．

さて，定数 \alpha を適切にえらぶと，

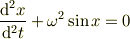
\frac{\mathrm{d}^2 x}{\mathrm{d}^2 t} + \omega^2 \sin x = 0

は

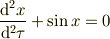
\frac{\mathrm{d}^2 x}{\mathrm{d}^2 \tau} + \sin x = 0

に書き換えられ，パラメータは方程式からすべて消すことができます．

\alpha の値は?

Re: 振り子の減衰について

K さんのレス (2009/02/06(Fri) 21:04)

d^2x/dt^2=(dτ/dt)α(d^2x/dτ^2)となるから，

α=1/(ω^2)でしょうか？

Re: 振り子の減衰について

toorisugari no Hiro さんのレス (2009/02/06(Fri) 21:11)

> d^2x/dt^2=(dτ/dt)α(d^2x/dτ^2)となるから，α=1/(ω^2)でしょうか？

？？？

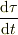\frac{\mathrm{d}\tau}{\mathrm{d}t} の値は?