連結Lie群
連結Lie群
snow さんの書込 (2009/02/01(Sun) 15:41)
連結Lie群の話なのですが, 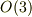 が連結であると仮定し,
単位元とつながっている元を
が連結であると仮定し,
単位元とつながっている元を  とすると,
単位元から
とすると,
単位元から  にいたる連続曲線があり,
にいたる連続曲線があり,
 の行列式の値は連続曲線に沿って連続的に変化するが
の行列式の値は連続曲線に沿って連続的に変化するが
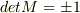 と離散的なので曲線に沿って変化できないので
と離散的なので曲線に沿って変化できないので 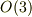 は連結でない.
とあるのですが,
>行列式の値は連続曲線に沿って連続的に変化する
この部分がよくわかりません.
教えてください.お願いします.
は連結でない.
とあるのですが,
>行列式の値は連続曲線に沿って連続的に変化する
この部分がよくわかりません.
教えてください.お願いします.
Re: 連結Lie群
toorisugari no Hiro さんのレス (2009/02/02(Mon) 12:13)
直交行列 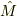 は,
は, 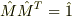 を満たすので
を満たすので 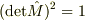 を満たします.
を満たします.
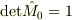 を満たす行列から出発して,
を満たす行列から出発して, 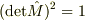 を満たしながら行列の要素を連続的に変化させても,
を満たしながら行列の要素を連続的に変化させても, 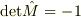 にする事はできません.なぜなら,行列式は行列要素の連続関数だからです.
にする事はできません.なぜなら,行列式は行列要素の連続関数だからです.
ということを言っています.
Re: 連結Lie群
snow さんのレス (2009/02/02(Mon) 13:31)
あの,もうちょっと詳しくお願いします. 行列式は行列要素の関数であることはわかりますが,連続関数なのはどうしてですか?
Re: 連結Lie群
toorisugari no Hiro さんのレス (2009/02/02(Mon) 15:31)
> 行列式は行列要素の関数であることはわかりますが,連続関数なのはどうしてですか?
行列式の定義を知らないの?
Re: 連結Lie群
anon さんのレス (2009/02/02(Mon) 16:24)
多項式は連続関数ですよね.
Re: 連結Lie群
snow さんのレス (2009/02/02(Mon) 16:47)
そうか.確かに
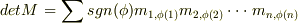 は多項式関数になりそうですね.
そして,多項式関数なら常に
は多項式関数になりそうですね.
そして,多項式関数なら常に 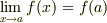 になるので連続ですか.
になるので連続ですか.
そして,すみません.
> 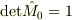 を満たす行列から出発して,
を満たす行列から出発して, 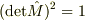 を満たしながら行列の要素を連続的に変化させても,
を満たしながら行列の要素を連続的に変化させても, 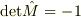 にする事はできません.
にする事はできません.
この部分もよくわかりません.連続関数だとなぜ無理なんでしょうか?
Re: 連結Lie群
anon さんのレス (2009/02/03(Tue) 13:25)
Lie群の勉強をするのですから, 位相空間について(連続写像の性質など)は既習なのですよね?
連続写像による,連結な位相空間の像は,やはり連結だということですよ.
Re: 連結Lie群
snow さんのレス (2009/02/03(Tue) 16:44)
いえ,位相空間は全くやってません.
猪木・川合の「量子力学?」に群論のことが書いてあるので
それを読んでいてわからないところがあったので質問をしています.
ちなみに,今回の質問内容はp235に書いています.
やっぱり,位相空間をやってから群論をやるべきですか?
(そういえば, 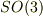 と
と 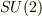 が同型でなのは異なるトポロジーを持つからって書いてあったなあ.)
が同型でなのは異なるトポロジーを持つからって書いてあったなあ.)
Re: 連結Lie群
toorisugari no Hiro さんのレス (2009/02/03(Tue) 17:57)
> 位相空間をやってから群論をやるべきですか?
位相空間を理解できてるのなら,今回の問題のイメージは容易にできるはずですが,位相空間を学習しておく必要はありません.
連続とは何かを正しく理解していればよいのです.
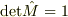 から
から 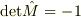 に実数の範囲で連続に変化するためには,必ず
に実数の範囲で連続に変化するためには,必ず 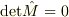 を通過する必要がある.しかし,これは条件
を通過する必要がある.しかし,これは条件 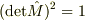 を破ってしまう.よって,
を破ってしまう.よって, 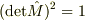 の下で,
の下で, 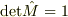 から
から 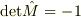 に実数の範囲で連続に変化することはありえない.
に実数の範囲で連続に変化することはありえない.
という事は特別な知識がなくとも理解できると思いますが....
Re: 連結Lie群
snow さんのレス (2009/02/03(Tue) 18:06)
あ!!そうですね.こんなことがわからない私って・・・. とにかく,ありがとうございます.
Re: 連結Lie群
toorisugari no Hiro さんのレス (2009/02/03(Tue) 21:22)
> こんなことがわからない私って・・・.
ま,余り落ち込まずに,次はもっと深く考える決意を固めてもらえばよいです.
> あ!!
この「あ!!」って感覚が,勉強の原動力になります.
# ついでに,直交行列ではなくユニタリ行列ならどうなるか,考えてみてください.位相という概念が大事な事が分かってもらえると思います.
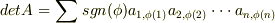
 は互換です.
は互換です.