相対論の質問
相対論の質問
hirokun さんの書込 (2009/02/01(Sun) 11:09)
はじめまして.本州の端で物理を勉強している大学生です.初めての投稿になります.よろしくお願いします.相対論で以下の3題が先日の授業で出たのですが,解答の方針がつかめなく困っています.できれば解答がこのようになるのでは?というような解答もいただけたらと思います.よろしくお願いします.
問
1,2次元平面(注:曲座標で行うこと)
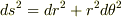 でリーマン曲率がすべて0であることを示せ
でリーマン曲率がすべて0であることを示せ
2,2次元球面
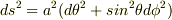 のリーマン曲率を求めよ
のリーマン曲率を求めよ
3,計量が, 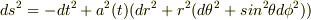 (
( 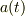 はスケールファクター)
のとき,アインシュタイン方程式をaの微分方程式として書け.
ただし
はスケールファクター)
のとき,アインシュタイン方程式をaの微分方程式として書け.
ただし 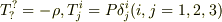 (注:Pは圧力,
(注:Pは圧力, 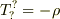 の添え字?は公表されませんでした. )
の添え字?は公表されませんでした. )
Re: 相対論の質問
Yokkun さんのレス (2009/02/01(Sun) 18:05)
>今,自分で解いてはみたのですが,答えがあっているか不安です.
ぜひご自分の解答を紹介された上で,どういった点が不安なのか書いてください.
Re: 相対論の質問
toorisugari no Hiro さんのレス (2009/02/02(Mon) 19:24)
まず, 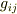 を求めてください.(1)(2)の場合2×2の行列ですから,簡単ですね.さらに
を求めてください.(1)(2)の場合2×2の行列ですから,簡単ですね.さらに
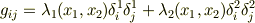
の形になるので,これを使って,素直に, 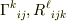 を計算していくしかないでしょうね.
を計算していくしかないでしょうね.