不等式
不等式
snow さんの書込 (2009/01/31(Sat) 19:33)
この不等式がよくわかりません. 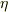 は実数で
は実数で  は複素数.
は複素数.
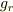 ,
, 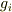 はそれぞれ
はそれぞれ  の実部と虚部です.
の実部と虚部です.
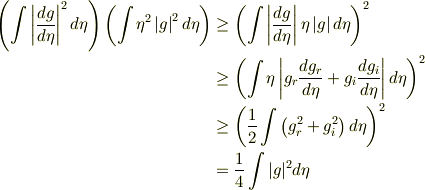
最初の不等式はシュバルツの不等式だと思うのですが,あとがよくわかりません. 証明をしていただけるとうれしいです.最後の等号もわかりません. お願いします!!
Re: 不等式
toorisugari no Hiro さんのレス (2009/01/31(Sat) 19:41)
式が長すぎて,表示に困ります.改行などを入れて,幅を短くしてください. あと,第2式と第5式(最終式)は違うように思いますが,書き写し間違いをしていませんか?
あと,括弧や絶対値はleft(...right)やleft|...right|とすると見やすくなります.
Re: 不等式
snow さんのレス (2009/01/31(Sat) 20:20)
すみません. えーと,第2式は写し間違えです.第5式はこうなってました.第5式はやっぱり変ですよね.
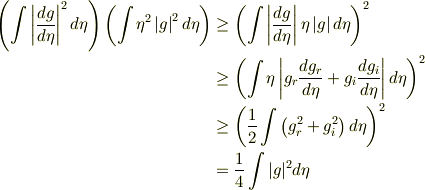
あの,左に詰めるにはどうすれば・・・.
Re: 不等式
toorisugari no Hiro さんのレス (2009/01/31(Sat) 20:32)
> あの,左に詰めるにはどうすれば・・・.
& を使います.
<Tex> 式 &= 式\ &> 式\ &> 式 </Tex>
ついでですから,最初の記事を修正してください.
Re: 不等式
toorisugari no Hiro さんのレス (2009/01/31(Sat) 21:03)
第一不等式は実関数のシュワルツの不等式,
第二不等式は, 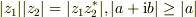 ,
第三不等式は部分積分
第四等式は意味不明.
,
第三不等式は部分積分
第四等式は意味不明.
Re: 不等式
toorisugari no Hiro さんのレス (2009/01/31(Sat) 21:24)
> もし,第4等式が...なら,あってますよね?
たぶん.他に条件はないのですね. あと,「第三不等式は部分積分」と書きましたが,きちんと導出してないので確かめてくださいね.
Re: 不等式
snow さんのレス (2009/01/31(Sat) 21:52)
部分積分するとき中身が絶対値の場合は積分項はプラスになるのですか? 通常はマイナスですが・・・.
Re: 不等式
toorisugari no Hiro さんのレス (2009/02/02(Mon) 12:28)
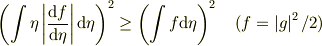
これの証明,分かりませんね.どなたかHELPおねがいます. # 絶対値がなければ簡単なんだけど...
