行列要素の添え字

行列要素の添え字

ファイル さんの書込 (2009/01/30(Fri) 04:00)

くだらないことかもしれませんが，変なところに嵌ってしまって悩んでいます． 共変ベクトルの変換 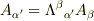A_{\alpha'}={\Lambda^{\beta}}_{\alpha'}A_{\beta} の変換行列Λを書き下すと，行と列の関係が通常の行列と逆になってしまうんです．行列の掛け算の定義は 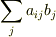\sum_{j}a_{ij}b_{j} なので，(添え字が隣同士でないといけないんですよね．)当然といえば当然なのですが，この行列だけ逆なのが気持ち悪くて・・・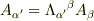． A_{\alpha'}={\Lambda_{\alpha'}}^{\beta}A_{\beta} とするのはどうだろう？と思ったのですが，そうすると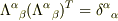， {\Lambda^{\alpha}}_{\beta}({\Lambda^{\alpha}}_{\beta})^{T}={\delta^{\alpha}}_{\alpha} の関係を満たさないことになってしまいます． 行列の添え字は{ij}の順番に，「行，列」と覚えていたのですが，それがそもそも間違いだったのでしょうか？

Re: 行列要素の添え字

Yokkun さんのレス (2009/01/30(Fri) 09:02)

私も最初はだいぶとまどいました． でもこの積の順序を気にしなくていいところが添字による成分表示の便利なところでもあります．

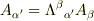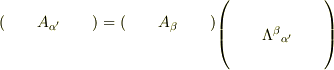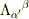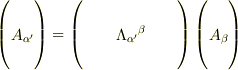
どうしても行列表示したければ， A_{\alpha^\prime}={\Lambda^\beta}_{\alpha^\prime}A_\beta は，おっしゃるとおり (\qquad A_{\alpha^\prime}\qquad)=(\qquad A_\beta\qquad)\begin{matrix}\\\left(\begin{matrix}\\\qquad{\Lambda^\beta}_{\alpha^\prime}\qquad\\ \,\end{matrix}\right)\end{matrix} とすればいいのかな？もちろん， {\Lambda_{\alpha^\prime}}^\beta もありだと思いますよ． \begin{pmatrix}\\ A_{\alpha^\prime}\\\,\end{pmatrix}=\left(\begin{matrix}\\\qquad{\Lambda_{\alpha^\prime}}^\beta\qquad\\ \,\end{matrix}\right)\begin{pmatrix}\\A_\beta\\\,\end{pmatrix}

本来，行列表示した際，行と列の区別に絶対的な意味はないと思います． 行列積で，左因子の行ベクトルと右因子の列ベクトルの成分の積和をとるという計算ルールによるしばりが生じるだけでしょう．

Re: 行列要素の添え字

ファイル さんのレス (2009/01/31(Sat) 22:18)

なるべく，成分表示で進めたほうが混乱が少なそうですね． ありがとうございました．

Re: 行列要素の添え字

Yokkun さんのレス (2009/01/31(Sat) 23:01)

行列表示は視覚的に和の構造がはっきりして，私も好きなのですが， いずれクリストッフェル記号や曲率テンソルなどを扱うことになれば それもかなわなくなりますよね．３次元，４次元の行列（？）になります．