回転楕円体上の2点を通る大円の式
回転楕円体上の2点を通る大円の式
ぽてとぐらたん さんの書込 (2009/01/25(Sun) 17:47)
地球を球近似せず回転楕円体と考えたとき,地球上の2点を結ぶ最短経路を含む楕円の方程式はどのように記述されるかについてなのですが,以下のような素人考えでよいか,又はもっと分かりやすいエレガントな記述がありましたら誰か教えてください.
地球の回転楕円体の方程式は直交カルテシアン座標系で書くと(z軸は自転軸,x軸,y軸は赤道面上の直交する2軸)
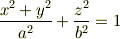
なお,  は長径(赤道円周の半径),
は長径(赤道円周の半径),  は短径(北極と南極を結んだ直線の長さの半分)とします.
は短径(北極と南極を結んだ直線の長さの半分)とします. 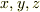 をa,b,緯度
をa,b,緯度  ,経度
,経度  で表すとそれぞれ,
で表すとそれぞれ,

です.
問題となる2点を通る楕円は地球の赤道面(正円)をまずz軸回りに  だけ回転し,次いでy軸回りに
だけ回転し,次いでy軸回りに  だけ回転した面上にあると考えられます.上記xyzの座標系に
だけ回転した面上にあると考えられます.上記xyzの座標系に  ,
,  の回転行列を掛けて得られる新しい座標の組x',y',z'は,長くなるのでまじめに書くのを省きますが,
の回転行列を掛けて得られる新しい座標の組x',y',z'は,長くなるのでまじめに書くのを省きますが, 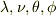 の4つの変数を含むことになります.
の4つの変数を含むことになります.
ここで,この平面上に乗る一般的な楕円の式は
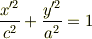
(*なお,この楕円の長径・短径のいずれかは  のままで.もうひとつのは
のままで.もうひとつのは
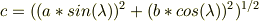
と表されるはず)
で,やはり 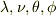 の4変数から成っています.
の4変数から成っています.
これに既知の2点の緯度・経度  ,
,  を代入すると,
を代入すると, 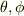 に関する2本の連立方程式になり,
に関する2本の連立方程式になり, 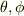 を求めることが出来るので,楕円の方程式が分かる.
を求めることが出来るので,楕円の方程式が分かる.
実際に解くとなるとかなりめんどくさいかもしれませんが,仮定に間違いはないでしょうか? で,そもそも最短経路(測地線)と云うのは上記のように仮定した楕円の上に乗るものなんでしょうか?
地球上の測地線(geodesic on the Spheroid)についてちょっと調べてみました(wikipediaなど)が,アフィン接続?だか何だかでかなり高度なように見受けられました.一般的な任意の球体について測地線を定義するとかなり難しくなるのだと思いますが,地球の場合はかなり単純化出来る回転楕円体なので,測地線は上記のようにして求められる楕円の上に乗る,と云えないかなあと思ったのですが,いまいちはっきりしません.また,2点を結ぶ楕円(なり測地線)の方程式をもっとエレガントに記述できる方法がありましたらお尋ねしたい次第です.(なお,2点のいずれかが北極点・南極点となるようなことはなしとします)どなたかよろしくお願い致します.
Re: 回転楕円体上の2点を通る大円の式
yama さんのレス (2009/01/25(Sun) 20:48)
「2点を結ぶ最短経路を含む楕円の方程式」ということは,2点を結ぶ最短経路が楕円の一部であることが前提になると思いますが,その前提が成り立つかどうか疑問です. この場合の測地線は,たぶん一平面上にはなく,従って楕円にはならないように思われます.
Re: 回転楕円体上の2点を通る大円の式
ぽてとぐらたん さんのレス (2009/01/26(Mon) 08:22)
ご回答をありがとうございます.仰るとおり, >この場合の測地線は,たぶん一平面上にはなく と云う可能性もありますので,一般的にはこのような問題は非常に難しいものになります. しかし,球面上の2点の最短経路が大円の一部であるが故に問題が簡単に解けるように, 球を上下からつぶしたくらいのみかん型の回転楕円体(oblate spheroid)においては,最短経路は2点を通る楕円の一部でよい,と云う結論(もしくはyamaさんが仰るように,「そうはならない」と云うはっきりした結論)がどこかに落ちていないかなあ?と考えた次第です.証明はもちろん易しくないとは思いますが.
Re: 回転楕円体上の2点を通る大円の式
yama さんのレス (2009/01/26(Mon) 23:38)
厳密な証明は難しいと思いますが,直観的には次のように考えることができると思います.
球面上では大円に沿って,たるまないように糸を巻き付けて一周させることができます.もし楕円体の測地線が楕円であれば,同様にその楕円に沿ってたるまないように糸を巻き付けて一周させられるはずですが,実際にはできないと思います.
例えば,扁平率の大きい回転楕円体として碁石のようなものを考えます. それに糸を巻き付けて一周させようとしても,すっぽぬけてしまって一周させることはできないでしょう.例外的な場合として赤道や子午線に沿って巻き付けることはできますが一般にはできないでしょう.
それでは碁石表面の測地線は実際はどうなるのか考えてみましょう. 碁石の表面の任意の2点A,Bを考えます.簡単のため2点とも表側にあるものとします. A点に糸の端を固定し,B点に向かって引っ張りながら糸を伸ばすと,それがAB間の測地線になるはずです.さらにそのままずれないように糸を延長して裏側に回してから再び表側に戻します.そのとき戻ってきた糸は初めのAB間の測地線には重ならないでしょう.さらに糸を延長していくと,表側に戻るたびに位置がずれながら,ぐるぐると碁石に巻きつくと思います. この糸の経路が測地線になるはずですが,これは一平面上にはなく,捩率をもった曲線になるでしょう.
Re: 回転楕円体上の2点を通る大円の式
yama さんのレス (2009/01/28(Wed) 23:46)
測地線の式を具体的に求めるには次のような方法が考えられます.
一般に曲面上に束縛された質点に外力が働かないとき,質点の軌道は測地線になります.
従って楕円面上の質点に外力が働かないときの軌道を求めればよいわけです.
そのためには,運動エネルギーを緯度  と経度
と経度  およびそれらの時間微分を用いて表します.
外力が働かないときは,これがそのままラグランジアンになるので,ラグランジュ方程式をつくれば,それが運動方程式です.
その運動方程式を解けば,測地線が時間をパラメータとする式で表されることになります.
およびそれらの時間微分を用いて表します.
外力が働かないときは,これがそのままラグランジアンになるので,ラグランジュ方程式をつくれば,それが運動方程式です.
その運動方程式を解けば,測地線が時間をパラメータとする式で表されることになります.
Re: 回転楕円体上の2点を通る大円の式
mNeji さんのレス (2009/01/29(Thu) 00:26)
横から失礼します.お二人の論議を興味深く拝見させて頂いています.
>一般に曲面上に束縛された質点に外力が働かないとき,質点の軌道は測地線になります. >従って楕円面上の質点に外力が働かないときの軌道を求めればよいわけです.
この場合,回転楕円体は「密度一定な質量分布」を仮定しているのではないでしょうか.
また,球体では,重力と抗力(摩擦力がないと仮定)とは動径方向だけでバランスできます.が,回転楕円体では,先験的にバランス出来ないように思われます.すると,場所毎に重力の影響が陽に出て来るのではないでしょうか?
Re: 回転楕円体上の2点を通る大円の式
yama さんのレス (2009/01/29(Thu) 07:19)
外力が働かないということは,重力も働かないということです.ただし,拘束力は働きます. 実際の地球上の運動ではなく,仮想的な運動を考えるわけです.
Re: 回転楕円体上の2点を通る大円の式
mNeji さんのレス (2009/01/29(Thu) 08:59)
>外力が働かないということは,重力も働かないということです.ただし,拘束力は働きます.
確かに,そのような抽象的な問題設定もあるかも知れませんが....
でも,スレッドの冒頭で,
>地球を球近似せず回転楕円体と考えたとき,地球上の2点を結ぶ最短経路を含む楕円の方程式
とあるので,地球の形状が遠心力により,球形からオブレート変形を受けたと仮定して,その場合の最短経路を求めるのが課題かと感じました.
Re: 回転楕円体上の2点を通る大円の式
mNeji さんのレス (2009/01/29(Thu) 12:58)
>考えている「表面」を二つを合わせたポテンシャルの等値面と定義すれば,外力はないですね.ただし,「表面」は正確には回転楕円体ではないです.
確かに,そう考えられますか....「回転楕円体」から出発する,という点から見ても,細かく気にしすぎたかと,思いました.
># 地球の様に自転してる場合を考えるのが簡単かもしれませんが,この場合はコリオリ力を考慮しなければいけないので,不適切です.
御意.
私の横からの質問はこれにて終了します.失礼しました.
Re: 回転楕円体上の2点を通る大円の式
toorisugari no Hiro さんのレス (2009/01/29(Thu) 15:16)
すいません.mNejiさんがreplyされた記事は,式が納得いかなかったので,消してしまいました. #タイミングの問題でreplyされてしまいました.
逆二乗の力と遠心力は共に保存力なので,その合力のポテンシャルの等値面を表面と考えれば,外力は0という話です.
Re: 回転楕円体上の2点を通る大円の式
ぽてとぐらたん さんのレス (2009/02/09(Mon) 00:11)
長いこと返信をせずにおりました...申し訳ございません. yama様の碁石に糸を巻きつけてゆく,の喩えは大変分かりやすく,なるほど,と思いました. また,ラグランジュ方程式による測地線の同定についても納得しました.
また,地球の表面をどこに定義するか,と云うのは実際難しい問題でして,現在はWGS-84と云う米国が1984年に作った地球の等ポテンシャル面を表面と定義しているそうです.これでGPSやら何やらの海抜高度が定義されます.
皆様,ありがとうございました.これにて本トピック終了したいと思います.