偏微分方程式
偏微分方程式
夏 さんの書込 (2009/01/24(Sat) 11:51)
こんにちは.大学3回生です.
次の第一種初期値・境界値問題を解け.
∂u(x,t)/∂t = ∂^2 u(x,t)/∂x^2
u(x,0) = π/2 + x + 4(cosx)^3
u(-π/2,t) = 0, u(π/2,t) = π
という問題です. 放物型方程式なので,参考書で放物型方程式のところを調べてみたのですが, 初期条件がどちらも0の場合しか載っていませんでした. もし初期条件がどちらも0とすれば, まず0〜πの範囲になるように uをx方向にπ/2だけずらしたものをVと置いて, 初期条件f(x) = x + 4(sinx)^3として, 変数分離をして解けば Vn(x,t) = Bn・sin(nx)・e^(n^2)t V(x,t) = ΣVn(x,t) f(x) = ΣBn・sin(nx) xはsinでフーリエ展開できて, 4(sinx)^3 = 3sinx - sin3x とできるのでBnが決定できる… という感じかなと思いました. 全然違っていたらごめんなさい. 境界が0の場合を使うのかなと思ったのですが どう使っていいのか分かりません…. どなたか教えて下さい,宜しくお願いします.
Re: 偏微分方程式
toorisugari no Hiro さんのレス (2009/01/24(Sat) 14:44)
> 次の第一種初期値・境界値問題を解け.
> という問題です.
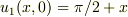 はどのような境界条件を満たしますか?時間発展はどうなりますか?
はどのような境界条件を満たしますか?時間発展はどうなりますか?
境界条件が

となる二つの解 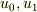 の線形和
の線形和 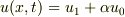 は,境界条件
は,境界条件 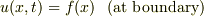 を満たす解になります.
を満たす解になります.
この考えを使えばいいのでは?
後,時間発展については,初期条件を
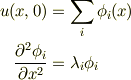
となる(一次独立な)2階微分の固有関数 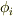 の線形和で表せば,
の線形和で表せば,
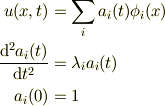
となる 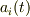 を求めることになります.
を求めることになります.
Re: 偏微分方程式
夏 さんのレス (2009/01/24(Sat) 21:58)
>toorisugari no Hiro様 御回答有難うございます! つまり,
uo(x,t) = 4(cosx)^3
u1(x,t) = π/2 + x
と置く,と言う事ですよね. でもそれだと,uoの方は確かに
uo(-π/2,t) = uo(π/2,t) = 0
となって境界での値が0になりますが,u1の方は
u1(-π/2,t) = 0u1(π/2,t) = π
となって,境界での値が異なってしまいます…. もしかしたら自分が何か勘違いしているのかもしれません, もう一度そのやり方で考え直してみます….
Re: 偏微分方程式
なんとなく さんのレス (2009/01/25(Sun) 18:30)
夏さん,初めまして,なんとなくです.
>Hiroさん 横やりすみません.
懐かしい演習問題を見たような気がして興味があったので,参加したくなりました.教えるというより,一緒に考えさせてくださいね. 夏さんのように,x'=x+π/2と置いて,x'=xと読み替えると ∂u/∂t=∂^2u/∂^2x,u(0,t)=0,u(π,t)=π,u(x,0)=x+4sin^3x となりますので,これで考えます. 一般的な境界条件ではu(π,t)=0がよく出てきますが,初期条件式のxにπを代入すれば,u(π,0)=π+4sin^3(π)=πとなって,解にxを含むことが示唆されます. また,u(0,t)=0より離散化条件が出ますから,整数nの結合で解を作ればいいでしょう. したがって,夏さんが始めに思われたような変数分離形のよる解法に従うと境界条件から u(x,t)=x+ΣBnexp(-n^2t)sin(nx){n=1,2,…}なる形が予想されます. 後は,Bnを調整すればどうでしょう. ただ,時間発展部分は変数分離形の共通定数を負(-n^2)にしないと,境界条件が生かせなくなります.
Re: 偏微分方程式
toorisugari no Hiro さんのレス (2009/01/26(Mon) 16:00)
> u1の方は > u1(-π/2,t) = 0u1(π/2,t) = π > となって,境界での値が異なってしまいます….
だから,うまくいくのでしょう?
これって,非同次線形方程式の解き方と似ています.非同次線形方程式を満たす特解を取り除けば,同次線形方程式になってしまいますよね.
0以外の境界条件を満たす特解を取り除けば,境界条件0の問題になってしまいます.
u1がどのような時間発展をするかが分かれば簡単です.
Re: 偏微分方程式
夏 さんのレス (2009/01/27(Tue) 03:53)
>なんとなく様 解答有難うございます! 無事解く事ができました. 境界条件もきちんと満たしているので 大丈夫だと思います!
>toorisugari no Hiro様 「非同次線形方程式の解き方と似ている」という説明で やっと意味が分かりました! 無事解く事ができたみたいです. 有難う御座いました!
Re: 偏微分方程式
toorisugari no Hiro さんのレス (2009/01/27(Tue) 12:23)
> 「非同次線形方程式の解き方と似ている」という説明で やっと意味が分かりました!
^^)
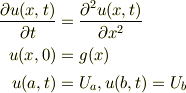
という問題は,
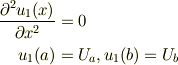
を満たす特解 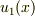 が分かれば,
が分かれば, 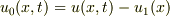 とおいて,
とおいて,
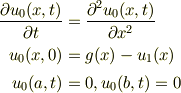
という問題にかわるということですね.