剛体振り子

剛体振り子

タマゴ さんの書込 (2009/01/23(Fri) 03:55)

質量Ｍの剛体を支点Ｏを中心に単振動させるとき，これを剛体振り子

と呼ぶ．いま，水平軸(支点)の周りの慣性モーメントＩとすると，

この剛体振り子の回転運動の方程式は

Ｉdθ^2/dt^2=-Mghsinθ・・・・・?となる．

ここで近似式sinx=xと近似できるとき，?式を用いて

剛体振り子の周期Ｔは，

Ｔ＝2π√(Ｉ/Ｍgh)と求まることを証明せよ．

という問題がまったく分かりません．どなたか教えてください．

Re: 剛体振り子

toorisugari no Hiro さんのレス (2009/01/23(Fri) 06:15)

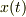以下の問題を解いてください． 「 質量 m の質点がバネ定数 k のバネにつながれ単振動している．つりあいの位置を原点，時刻 t における質点の位置を x(t) として，質点の運動方程式，および，単振動の周期 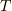T をもとめよ． 」 わからないのなら，教科書を読み直して勉強してください．

Re: 剛体振り子

mNeji さんのレス (2009/01/23(Fri) 11:49)

すこしインチキな説明をしてみます．

＞この剛体振り子の回転運動の方程式は ＞Ｉdθ^2/dt^2=-Mghsinθ・・・・・?となる． ＞ここで近似式sinx=xと近似できるとき，?式を用いて

逆手をとって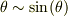， \theta \sim \sin(\theta)

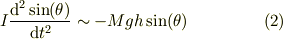
I\frac{\mathrm{d}^2 \sin(\theta)}{\mathrm{d} t^2 } &\sim -Mgh\sin(\theta) &(2)

そして，角度が時間tの一次式で，周期Tと仮定，

\theta &= \frac{2\pi}{T}t &(3)

すると，式(2)の左辺の時間微分は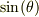， \sin(\theta) の時間微分が，

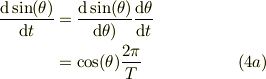
\frac{\mathrm{d} \sin(\theta)}{\mathrm{d} t}&= \frac{\mathrm{d} \sin(\theta)}{\mathrm{d} \theta)}\frac{\mathrm{d} \theta}{\mathrm{d} t}\\&= \cos(\theta) \frac{2\pi}{T} &(4a)

同様に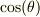， \cos(\theta) の時間微分は；

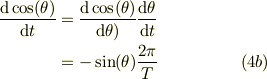
\frac{\mathrm{d} \cos(\theta)}{\mathrm{d} t}&= \frac{\mathrm{d} \cos(\theta)}{\mathrm{d} \theta)}\frac{\mathrm{d} \theta}{\mathrm{d} t}\\&= -\sin(\theta) \frac{2\pi}{T} &(4b)

合わせると，

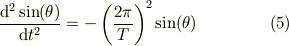
\frac{\mathrm{d}^2 \sin(\theta)}{\mathrm{d} t^2} &= -\left( \frac{2\pi}{T} \right)^2 \sin(\theta) & (5)

となるので，式(2)の左辺に代入して，両辺の 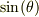\sin(\theta) の係数を比較すると，

I\left[-\left( \frac{2\pi}{T} \right)^2 \right] = -Mgh

となります．これを周期Tについて解けばいいのだろうとおもいます．