γの決定問題
γの決定問題
フジモリ さんの書込 (2009/01/21(Wed) 13:28)
他事多忙でレスが滞りすみません.怠けているうちに前スレ「No.20100 時空比普遍の定理結論」がお蔵入りしてしまいました.
>(yamaさん) 特別な条件は仮定しないで,相対性や対称性だけを用いてC1,C2 がvに因らずに一定になることを導くことができるというのがフジモリさんの主張だったはずです
その通りです.以下に今迄と別の取組みを示します. x2=γ(v)(x1-v*t1)(1a)x1=γ(v)(x2+v*t2)(1b) γ(v)が決まれば座標変換対応が確定するので,どうγを決定するかという観点から取組みます. (1a)(1b) より,γ,v,t2を求めれば γ=(x1*t1+x2*t2)/(x1*t2+x2*t1)(2) v=(x1^2-x2^2)/(x1*t1+x2*t2) (3) t2=γ(t1-k*v*x1)(4) 但しk=(γ^2-1)/(γ^2*v^2)(5a)kはvの偶関数 またはγ^2=1/(1-k*v^2)(5b) ここでγ,vからkを計算すると k=(t1^2-t2^2)/(x1^2-x2^2)(6)この式を変形して x1^2-t1^2/k=x2^2-t2^2/k=(x2^2*t1^2-x1^2*t2^2)/(t1^2-t2^2)(7)
任意の(x1.t1)が(x2,t2)に変換される為にはk,γが決まればよいが,(6)(7)より x2/t2=±x1/t1=共通値(8) となれば共通値よりk,γが決まる. この共通値を3個の慣性系の対称性から別途考察しようというのが前回(No.22173)の提案でした.
Re: γの決定問題
toorisugari no Hiro さんのレス (2009/01/23(Fri) 06:36)
> 以下に今迄と別の取組みを示します.
まったく代わり映えしません.相変わらず,論理になっていません.
問題の入力と出力を明確にしないと論理になりません.
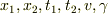 のうち入力となる量は何ですか?未知の量(=出力)は何ですか?また,入力となる量の値は「任意」ですか?「特別な値」ですか?
のうち入力となる量は何ですか?未知の量(=出力)は何ですか?また,入力となる量の値は「任意」ですか?「特別な値」ですか?
上のすべての量について,それぞれ 「任意な値」 「特別な入力値」 「未知の量」 のどれにあたるのか列挙してください. 「特別な入力値」の場合,その値(あるいは条件式)を併記してください.
# 「任意な値」はその値について指定も仮定も(式の値を仮定しても)いけません.できるのは「特別な入力値」の場合だけです.
以上をきちんと理解したら 「x2/t2=±x1/t1=共通値(8) となれば共通値よりk,γが決まる.」 なんて(0/0を計算に使うのと同じくらい)馬鹿なこと書けるはずがありません.
Re: γの決定問題
フジモリ さんのレス (2009/01/30(Fri) 13:23)
>問題の入力と出力を明確にしないと論理になりません
・v は慣性座標系S1からS2をみた速度である.S2からS1をみた速度は相対性により-v. ・γはvの未知関数でかつvの偶関数であり,v→0のときγ→1. ・(x1,t1)と(x2,t2)は慣性座標系S1とS2の座標対応点であり,連立方程式(1a),(1b)により相互に座標変換される.即ち任意な(x1,t1)→座標変換→(x2,t2)または(x1,t1)←座標変換←任意な(x2,t2) ・vの式(2)とγの式(3)は,何らかの方法により原点以外の座標対応点(x1,t1)と(x2,t2)がわかればv,γの従うべき関係式.
># 「任意な値」はその値について指定も仮定も(式の値を仮定しても)いけません
任意な値である座標対応点の特性や構造を検討することは問題ないと思います.
Re: γの決定問題
toorisugari no Hiro さんのレス (2009/01/30(Fri) 15:24)
>># 「任意な値」はその値について指定も仮定も(式の値を仮定しても)いけません >任意な値である座標対応点の特性や構造を検討することは問題ないと思います.
任意な二つの実数の組 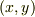 に,
に, 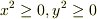 以外の構造や特性など存在しません.また,任意の量に後付で条件を付加するのも許されません.
自分勝手に数学をねじ曲げないでください.
#「任意」の意味を理解されていませんね.
以外の構造や特性など存在しません.また,任意の量に後付で条件を付加するのも許されません.
自分勝手に数学をねじ曲げないでください.
#「任意」の意味を理解されていませんね.
あなたの文面を整理すると,以下のようになります.
この問題では
(1)  は与えられた値です.この値は任意です.
(2)
は与えられた値です.この値は任意です.
(2) 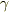 は
は  のある関数(
のある関数( 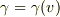 )で,
)で, 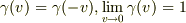 を満たす.
を満たす.
で,ここからが訂正が入ります.
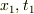 は任意の値.
は任意の値. 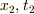 は(1a)(1b)より導出された式
は(1a)(1b)より導出された式
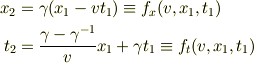
を満たす量.
つまり,
「
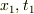 は任意の値,
は任意の値, 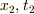 は
は 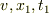 の関数.
」(見方A)
の関数.
」(見方A)
# なお,見方を変えて,
「
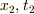 は任意の値,
は任意の値, 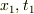 は
は 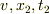 の関数.
」(見方B)
としても良いが,見方Aと見方Bは背反的なので「同じ論理内で両方使ってはいけません」.
ですから,「見方A」をとります.
の関数.
」(見方B)
としても良いが,見方Aと見方Bは背反的なので「同じ論理内で両方使ってはいけません」.
ですから,「見方A」をとります.
あなたの
「x2/t2=±x1/t1=共通値となれば共通値よりk,γが決まる.」
において, 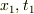 は任意ですから,「共通値」も任意であり,k,γは「任意」になり,γは決まりません.(これは見方Bを採用しても同じです.)
# あなたのこの文はつっこみどころ満載で困ります.
は任意ですから,「共通値」も任意であり,k,γは「任意」になり,γは決まりません.(これは見方Bを採用しても同じです.)
# あなたのこの文はつっこみどころ満載で困ります.
あなたの論理ははっきり言って出鱈目です.論理が汚いので,嘘が分かりづらく潜り込んでいて,あなたの書いた嘘に他ならぬあなたが騙されています.
# 最初に示した >任意な値である座標対応点の特性や構造を検討することは問題ないと思います. といった,何も知らない人なら信じてしまう,でも出鱈目な,嘘を,あなたはよく使われます.(あなたは,そういった嘘をつくことが「数学」あるいは「物理」だと,思われている節があります.)
このまま,自分に都合のよい出鱈目な数学「自称無手勝流」をお続けになるのでしたら,初学者の害になり,迷惑です.
今後の発表はご遠慮願います.
Re: γの決定問題
フジモリ さんのレス (2009/03/01(Sun) 00:57)
>>任意な値である座標対応点の特性や構造を検討することは問題ないと思います.
(修正)任意な値である座標対応点の変換の特性や構造を検討することは問題ないと思います.
># この文はつっこみどころ満載で困ります. >今後の発表はご遠慮願います.
馬鹿なやつが馬鹿な事を言っているかもしれませんが,つっこみどころはつっこめばよいのであって,相手の発言を封ずるのは管理人さんを通せばよい.そもそもyamaさんへのレスの途中であり,頻繁な投稿とならないように間隔をあけていた所です.
Re: γの決定問題
フジモリ さんのレス (2009/03/01(Sun) 00:59)
初頭の投稿2009/01/21(Wed) 13:28 No.22776の続きです.
(1a),(4),(5a)から直ちに,または(7)から k*x2^2-t2^2=k*x1^2-t1^2(7b) 直線上に3個の慣性座標系S1,S2,S3(x3,t3)を考え,S1からS2をみた速度をv1,同様の順序でv2,v3とする.同様の考え方で,γ1,γ2,γ3,k1,k2,k3を定義すると(7b)は次のように展開される. k1*x2^2-t2^2=k1*x1^2-t1^2(9a) k2*x3^2-t3^2=k2*x2^2-t2^2(9b) k3*x1^2-t1^2=k3*x3^2-t3^2(9c) (9a),(9b),(9c)の両辺を足し合わせて整理すると (k3-k1)*x1^2+(k1-k2)*x2^2+(k2-k3)*x3^2=0(10) (x1,x2,x3) の組合せは無数に存在するから k1=k2=k3 [=k vに依らない普遍定数] となり,γ(v)が決まる.(5b)より γ(v)=1/SQRT(1-k*v^2)(11)
普遍定数kの正負により次の場合に分類される. 1) k>0, γ>1 のとき,ローレンツ変換(1a),(4)を得る. γが実数となるための条件は(12)から 1-k*v^2>0 C=1/SQRT(k) とおけば -C<v<C(12) C は慣性系の相対速度v の上限を規定する最高速度で,すべての慣性系において同一である.(最高速度普遍則) 2) k=0, γ=1 のとき,(4)からt1=t2となり,ガリレイ変換(1a)を得る. 3) k<0, 0<γ<1のとき,時空座標軸の回転を得る.
Re: γの決定問題
yama さんのレス (2009/03/01(Sun) 09:38)
toorisugari no Hiro さんが指摘されたことを全く理解されずに,相変わらず以前と同様の間違いをされているのは残念です.
k1,k2,k3はx1,x2,x3の関数であって定数ではありません. そのためフジモリさんのようにこれらを座標に無関係な係数と見なすことはできません. 従ってk1=k2=k3が成り立つとはいえません.
Re: γの決定問題
toorisugari no Hiro さんのレス (2009/03/03(Tue) 22:46)
> つっこみどころはつっこめばよいのであって,
せっかくつっこんでも,フジモリさんは指摘を理解しないで同じ様な詭弁を繰り返すでしょ.議論する意味がないです.私が口を挟まなきゃいいとおっしゃりそうだけど,この掲示板に嘘を書かれるのを黙っていられません.指摘を受け入れ正しい論理の議論をされるか,それが嫌なら,ご自分のblogで発表してください.
Re: γの決定問題
mNeji さんのレス (2009/03/04(Wed) 00:13)
フジモリさん,初めまして.
始めから,ずっと拝見しています.私は,体を壊してリハビリテーションをしている内に,このサイトを知って拝見している内に,ボッートしていた頭も少しずつ復帰している老人です.
この論議に限らず,物理の解釈には色々な角度からのアプローチが在っても良いと思う一人です.それも,なるべく明確でイメージのし易い考え方を創って行くのは,初等者の勉学の質の向上に繋がると思います.
でも,フジモリさんの一連のご発言を拝見していると,どの点が「核となるアイデア」で,それから「何を主張しようとする」かの関係が判らないのです.
#お恥ずかしいことに,私は数学おんちですので,悪しからず.
例えば,数式で表現し切れないとしても,グラフを使って表現に工夫をするとかあるように思います.それをご自分のサイトに公開して,意見を募るのも一法かと思います.
その様な論議の中で,解り易い説明がついたら,改めて,この掲示版にスレッドを立たれたら如何ではありませんか?
Re: γの決定問題
フジモリ さんのレス (2009/03/22(Sun) 21:01)
>k1,k2,k3はx1,x2,x3の関数であって定数ではありません.
yamaさんの指摘は具体的で分かり易い. 慣性系では時空の一様性からγ(v)はvの関数であり,x,tの関数ではない. k=(γ^2-1)/(γ^2*v^2)(5a)kはvの偶関数 だから,kもまたvの関数であり,x,tの関数ではない,と言えます.
Re: γの決定問題
yama さんのレス (2009/03/23(Mon) 00:16)
そのvが v=(x1^2-x2^2)/(x1*t1+x2*t2) (3) と表されるので,kがx,tの関数になるわけです.
と書いてみたものの,そもそも(3)もおかしいですね.
>(1a)(1b) より,γ,v,t2を求めれば
とはどういうことでしょうか? 方程式が2つしかないのに,γ,v,t2の3つの未知数が求められるはずはないと思いますが・・・. 実際,(3)式ではvを求めたことにはなりません.(3)には求めるべき未知数であるt2が含まれているからです.
さらに言えば,vは座標系間の速度ですから,普通は任意の値を与えることができるパラメータであって,求めるべき未知数ではありません.
といっても,(3)を用いないでvを任意値としても(7b)は成り立つかもしれませんね. しかし,x1,x2,x3は互いに独立に任意の値をとれるわけではありません. x1を任意にとった場合,x2,x3は座標変換の式によって決まるので,x1に無関係な任意の値をx2,x3に与えることはできません.従って(x1,x2,x3) の組合せが無数に存在するとしてもx1,x2,x3が互いに独立でないのでk1=k2=k3が成り立つとは言えません.
また,もしk1=k2=k3が成り立つとしても,結局はローレンツ変換またはガリレイ変換が導かれるだけであって,時空比普遍の定理が証明されるわけではありません. フジモリさんが主張される時空比普遍の定理はx1/t1=x2/t2=x3/t3が常に成り立つということであって,k1=k2=k3が成り立つということではなかったはずです.
Re: γの決定問題
フジモリ さんのレス (2009/03/25(Wed) 21:32)
mNejiさん,初めまして.私は学会とは無縁で表現がスマートとはいきませんが,権威筋の受け売りを排し,自己流でもあくまで自分の頭で考えることを大切にする者です.ですから「特殊相対論は量子論がからまないかぎり数学的構造がはっきりわかっています」と言われても,そうかな?と無手勝流に考え,疑問が湧き出る訳です.
>どの点が「核となるアイデア」で,それから「何を主張しようとする」かの関係
「何を主張しようとする」かは始めから一貫して変わっていません(2008/05/14(Wed) 08:27の投稿).即ち慣性座標系の相対性に基づく対称性からローレンツ変換が導かれるということです. 「核となるアイデア」は(1a)(1b)(4)(5a)から直ちに(7b)が導かれるので,光速度不変の原理を適用しなくても(10)により全ての慣性系で同一の普遍定数の存在が証明され,それは慣性系の相対速度の上限を規定する最高速度である(最高速度普遍則),という結論です. yamaさんとの遣り取りが途切れてしまい,その継続として立てたスレッドです.目障りだったら無視して下されたし.
Re: γの決定問題
yama さんのレス (2009/03/25(Wed) 23:37)
時空比普遍の定理というのは,相対性や対称性を仮定すれば任意の(x1,t1)についてx1/t1=x2/t2が成り立つということでしたね.つまり(x1,t1)について何の条件も仮定することなく,無条件でx1/t1=x2/t2が成り立つということでしたね. これに対して,速度の普遍定数の存在というのは,ある特定の速度があってx1/t1がその速度に等しければx1/t1=x2/t2が成り立つということですね.この場合x1/t1がその特定の速度に等しくない場合は,x1/t1=x2/t2が成り立つとは言えないわけです.つまり無条件でx1/t1=x2/t2が成り立つとは言えないわけですね.
今回述べられている内容からすると,もはや時空比普遍の定理は主張されないということのようですね.そうだとすれば適切な判断だと思います.
しかしフジモリさんの理論によって普遍速度の存在が証明されたとは言えません. フジモリさんの計算は,私には非常に見通しが悪く分かりにくいのですが,(7b)は確かに成り立つようです. しかし(10)から普遍定数の存在は証明できません.すでに述べたようにx1,x2,x3は互いに独立でなく,座標変換の式によって互いに関係づけられているからです.
Re: γの決定問題
mNeji さんのレス (2009/03/26(Thu) 01:52)
フジモリさん,ご説明有り難うございます.
>「核となるアイデア」は(1a)(1b)(4)(5a)から直ちに(7b)が導かれるので,光速度不変の原理を適用しなくても(10)により全ての慣性系で同一の普遍定数の存在が証明され,それは慣性系の相対速度の上限を規定する最高速度である(最高速度普遍則),という結論です.
私の納得出来ない点は,「最高速度普遍則が成り立ったとしても,それは光速と言えない」という事です.アインシュタインさんの立場と違う点は,この一点にあるように感じます.
ですから,「慣性系の相対速度の上限を規定する最高速度」と「光速」の等価性を明瞭に示す事ができれば,興味深いと思います.
Re: γの決定問題
toorisugari no Hiro さんのレス (2009/03/27(Fri) 12:37)
> 権威筋の受け売りを排し,自己流でもあくまで自分の頭で考えることを大切にする者です.
格好良いことおっしゃっているおつもりなんでしょうが,現状は「教科書や専門書や他人の指摘が理解できないので,自分勝手な数学や物理をつくっている.」に過ぎないのでは?
上のせりふは「トンデモ」な方がよく使われるせりふです.ご自分のことを「トンデモ」あるいは「似非科学者」ではないとお思いでしたら,このせりふは今後使われないのが良いと思います.
また,権威のいう事を,無条件に受け入れるのは間違いですが,「無条件に否定する」のも間違いです.どちらも思考停止状態です.
教科書や専門書に書いてあることを正しく理解して,その上で問題点を指摘して,新たな提案をするのが,正しい「権威におもねらない」やり方です.
フジモリさんが今されているのはテルレツキーの手法の劣化コピーです.テルレツキーを越えるどころか,それ以前の初歩的な理解不足で転けているところです.
まず,テルレツキーの手法を正しく理解することから始めませんか? テルレツキーのやり方は冗長ですが,きれいにまとめれば,一つの記事ぐらいにはできます.そこから,新しい話を進めるべきです.
それをせずに,中途半端なつまみ食いで「新公式」や「新定理」を作ろうとしても,トンデモな戯言に終わってしまいます.
Re: γの決定問題
フジモリ さんのレス (2009/04/04(Sat) 16:10)
>もはや時空比普遍の定理は主張されないということのようですね.そうだとすれば適切な判断だと思います.
(1a),(1b)に本質的な関係が潜んでいるという直感から出発しました. 「(1a)*(1b)にγ(v)^2=γ(-v)^2 の条件を適用したとき時空比普遍の定理が成立する」というのは無理がある,その理由は(1a)*(1b)と必然性なく式の変形をしたためである,と思い至りました.yamaさんの数々のご指摘有難うございました.そこで(1a),(1b)から何らかの文字を消去する変形にしてその存在条件式を導こうと考えた結果が今回の(続きの)スレッドです.なお 「(1a)*(1b)にγ(v)^2=γ(-v)^2 の条件を適用したときC1=C2となる」の正しい解釈は,「γ(v)^2=γ(-v)^2 が成立する座標対応点は,C1=C2が成立する所である」でしょう.
>しかし(10)から普遍定数の存在は証明できません.すでに述べたようにx1,x2,x3は互いに独立でなく,座標変換の式によって互いに関係づけられているからです.
(10)に適当な(互いに独立でない)x1,x2,x3の値を代入してみれば,すぐにk1=k2=k3 が導けます.釈迦に説法とは思いますが,以下証明です. x1=x2=1 のとき,(10)から (k2-k3)(x3^2-1)=0 即ちx3=±1またはk2=k3 また,x1,x2,x3,t1,t2,t3の連立方程式から (γ1*x1-x2)(γ2*x2-x3)(γ3*x3-x1)=(x1-γ1*x2)(x2-γ2*x3)(x3-γ3*x1)(13) が成立するので(証明略),この式にx1=x2=1 ,x3=±1を代入すると,1=-1となり矛盾する.よってx3≠±1従って k2=k3.同様にk1=k2となり,結局k1=k2=k3[=k vに依らない普遍定数で,全ての慣性系に拡張可] となる.
ローレンツ変換(1a),(4)の右辺に x1=C*t1 の関係を代入すれば,左辺に x2=C*t2 の関係が得られることも,普遍定数の存在と矛盾しません.
Re: γの決定問題
yama さんのレス (2009/04/04(Sat) 21:01)
x1=x2=x3=1 の場合は,これを(10)に代入すると (k3-k1)+(k1-k2)+(k2-k3)=0 という恒等式が得られるだけで,k1=k2=k3 は得られません.
また x1=x2=1,x3=-1 は座標変換の式を満たさないので,この場合は(10)が成り立つとは言えず,従ってこれを(10)に代入しても無意味です.
そもそも,(1a),(1b)のような座標変換の式が成り立つと仮定して(10)が導かれたわけですから,座標変換の式が成り立てば,k1=k2=k3 であろうとなかろうと,自動的に(10)が成り立つはずです. 従って(10)から k1=k2=k3 であるとは言えないわけです.
また,(13)の左辺の符号を逆にすれば右辺になるので,(13)が成り立つのは両辺が0の場合だけです.このような限定的な場合にしか成り立たない式が座標変換の式から導かれるとは思えません. フジモリさんがどのように(13)を導かれたのか分かりませんが,どこかに計算の誤りがあるのではないでしょうか.
>ローレンツ変換(1a),(4)の右辺に x1=C*t1 の関係を代入すれば,左辺に x2=C*t2 の関係が得られることも,普遍定数の存在と矛盾しません.
(1a),(4)は特別な場合としてローレンツ変換を含む一般的な式です.ローレンツ変換は光速を普遍定数として含んでいるので,(1a),(4)は特別な場合として普遍定数を含んでいると言えます. 従って,(1a),(4)が普遍定数の存在と矛盾しないのは当然です. しかし,普遍定数の存在と矛盾しないことは,必ずしも普遍定数が存在することを意味しません.
Re: γの決定問題
フジモリ さんのレス (2009/04/10(Fri) 19:50)
いろいろな証明法がありますが,別法では x1=a, t1=b とすると,x2=γ1(x1-v1*t1)=γ1(a-v1*b), x3=γ3(x1+v3*t1)=γ3(a+v3*b) x1,x2,x3を(10)に代入すると (k3-k1)*a^2+(k1-k2)*{γ1(a-v1*b)}^2+(k2-k3)*{γ3(a+v3*b)}^2=0(10b) これが任意のa,bで成り立つためには k1=k2=k3 となる.
Re: γの決定問題
フジモリ さんのレス (2009/04/10(Fri) 20:07)
>「慣性系の相対速度の上限を規定する最高速度」と「光速」の等価性を明瞭に示す事ができれば,興味深いと思います.
mNejiさん,そこはどうしても人間の判断が入ると思います. (6)においてkを速度の次元をもつCで置き換えてn個の慣性系に拡張すると x1^2-(C*t1)^2=x2^2-(C*t2)^2=...=xn^2-(C*tn)^2(6d) この普遍定数Cを物理現象に求めれば, ?慣性系内で等方的かつ一様に速度Cで拡がる時空の現象 ?慣性系の速度が到達できないほどの高速現象 であり,電磁場や重力場の伝播現象と伝播速度 c が普遍定数 C を与えると考えられる.
従来マイケルソン-モーリーの光速測定実験は光速度不変の原理の証拠であったが,この方法では理論的予測の検証となる.アインシュタインは先を急いで,証明する代わりに光速不変の原理を設けたが,この相対性原理の抜け道を知っていれば,こちらを通ったと思います.
Re: γの決定問題
yama さんのレス (2009/04/10(Fri) 23:12)
>(k3-k1)*a^2+(k1-k2)*{γ1(a-v1*b)}^2+(k2-k3)*{γ3(a+v3*b)}^2=0(10b) >これが任意のa,bで成り立つためには >k1=k2=k3
(10b)が任意のa,bについて成り立つには a^2, b^2, ab の係数がいずれも0になる必要がありますが,フジモリさんはもしかすると,a^2の係数が0ということが k3-k1=0 だと考えられたのでしょうか? しかし a^2の係数は k3-k1 ではありません.というのは,(10b)の第2項と第3項を展開することによっても a^2 を含む項が生じるので,それらを合わせると a^2 の係数は k3-k1+(k1-k2)(γ1)^2+(k2-k3)(γ3)^2 となり,これを0と置いても k3=k1 は得られません.
前に述べたように,(座標変換の関係式さえ成り立てば)k1=k2=k3 であってもなくても必ず(10)が成り立つわけなので,(10)をどんなにひねり回しても k1=k2=k3 が出てくるはずはありません.
Re: γの決定問題
mNeji さんのレス (2009/04/11(Sat) 00:47)
フジモリさん,
>そこはどうしても人間の判断が入ると思います.
この判断は正しいと思います.私の推測では,光速の導入は別途にする必要があるという事です.
とすると,これまで延々としてきた論議が成立したとしても,ローレンツ変換をまだ出し切れていないと思います.
本来の目的は,ローレンツ変換を簡明に示す筈ですが,逆に見通しが悪くなっていませんか?
Re: γの決定問題
フジモリ さんのレス (2009/04/11(Sat) 13:36)
>(10b)が任意のa,bについて成り立つには a^2, b^2, ab の係数がいずれも0になる必要があります
高校数学の手法を思い出しました.順にabとb^2の係数がそれぞれ0になるから -(k1-k2)γ1^2*v1+(k2-k3)γ3^2*v3=0 (k1-k2)γ1^2*v1^2+(k2-k3)γ3^2*v3^2=0 これが同時に成り立つためには(k1-k2)を消去して (k2-k3)γ3^2*v3(v1+v3)=0 結局k2=k3となりk1=k2となります.
>(座標変換の関係式さえ成り立てば)k1=k2=k3 であってもなくても必ず(10)が成り立つわけなので
座標対応の関係式が系1⇔2,2⇔3,で成立すると共に3⇔1でも成立する効果を忘れていませんか.
Re: γの決定問題
yama さんのレス (2009/04/11(Sat) 18:21)
今回は k1=k2=k2 であることが何とか導けたようですね. お疲れさまでした.
ところで,フジモリさんは3つの座標系の間の座標変換を考えられたわけですが,残念ながらこれはオリジナルな方法とは言えません. toorisugari no Hiroさんが,No.23275で述べられているように,これは既にテルレツキーが用いた方法です. また,フジモリさんの推論や計算は,私にとっては極めて見通しが悪く,テルレツキーにとってかわるものだとは思えないのは残念です.