ｎ×ｎ行列の対角化

ｎ×ｎ行列の対角化

tom さんの書込 (2009/01/21(Wed) 11:40)

こんにちわ大学１年生です．

１１１ １１１・・・ １１１ ・ ・

のようにすべて１からなるｎ×ｎ行列の対角化について質問です． １．固有方程式を解く以外に固有値を求める方法はありますか？ ２．固有値はｎと(ｎ−１)個の重複した０になると思うのですが， 固有値０に対する固有ベクトルにシュミットの直行正規化を何度も行って変換行列Ｕを求めることはとても骨が折れます，，，(例えば９×９行列のとき) そこで，変換行列を求めずに一般化して対角化する方法はありませんか？

最終的な答えは対角線上の１つにｎが入り，残りはすべて０の行列になると思うのですがいきなりそれを答えとして書くのはまずいですよね？

Re: ｎ×ｎ行列の対角化

mNeji さんのレス (2009/01/21(Wed) 12:30)

＞すべて１からなるｎ×ｎ行列

これって，「すべて平行な直線」がn本あると言う問題と同じになりませんか？逆に言えば，解は存在しませんね...．

Re: ｎ×ｎ行列の対角化

anon さんのレス (2009/01/21(Wed) 15:45)

tomさんの仰るとおり固有値は，n（重複度1）と0（重複度n-1）ですね．

固有方程式を書き下してそれを解くのはさほど難しくもなさそうですが， 他の方法がいいというのはどういう意図なのでしょうか．

もとの行列と共役な対角行列のことを「最終的な答え」と表現されていますから， 求めたいのはこの対角行列なのでしょうか． もしもそうであれば，変換行列などを求める必要はないと思います． そうではなくて，変換行列も必要だという場合でも， 用途によっては直交行列にしなくても正則行列でありさえすればよいということも あろうかと思います．正規直交化は必要なのでしょうか．

Re: ｎ×ｎ行列の対角化

Yokkun さんのレス (2009/01/21(Wed) 22:24)

>固有方程式を書き下してそれを解くのはさほど難しくもなさそうですが，・・・

たとえば，第 k 行から第 k-1 行を引く操作を下から順に施して，

\left|\begin{matrix}x-1&-1&-1&\cdots&-1\\-1&x-1&-1&\cdots&-1\\\vdots&\cdots&\ddots& &\vdots\\\vdots&\cdots&\cdots&\ddots&\vdots\\-1&\cdots&\cdots&\cdots&x-1\end{matrix}\right|=\left|\begin{matrix}x-1&-1&-1&\cdots&-1\\-x&x&0&\cdots&0\\0&\ddots&\ddots& &\vdots\\\vdots&\cdots&\ddots&\ddots&\vdots\\0&\cdots&\cdots&-x&x\end{matrix}\right|=(x-1)x^{n-1}-(n-1)x^{n-1}=(x-n)x^{n-1}

などとすればいいですね？

Re: ｎ×ｎ行列の対角化

mNeji さんのレス (2009/01/21(Wed) 23:53)

なるほど，固有値問題としては解があるのは判りました．n=2の場合，固有ヴェクタも存在しますね．

とすると，物理的にはどんな場合に応用出来るのでしょうか？宜しかったら，お教え下さい．

Re: ｎ×ｎ行列の対角化

tom さんのレス (2009/01/22(Thu) 09:28)

>anonさん すいません，固有方程式以外というのはとくに意図はありません・・

正規直交化しようとしたのは，これが直交行列を用いて対角化せよという問題だったからなんですが，わかりにくくてすみません．

>Yokkunさん なるほど，こうすればうまく解けますね．ありがとうございます．

Re: ｎ×ｎ行列の対角化

anon さんのレス (2009/01/22(Thu) 11:54)

> 直交行列を用いて対角化せよという問題 ということであれば，「最終的な答え」という表現が適切ではなかっただけですね．

シュミットの正規直交化は， どのベクトルの組からはじめるかで計算の面倒さが変わってきますね． まじめに実行するよりも，特徴をつかんでうまい組を選ぶことができれば楽ですね． また，正規化と直交化を同時に進めるのではなくて， 正規化は後回しにしたほうが計算が簡単です．

そこで，固有値nに対する固有ベクトルを(1,1,1,1,1,...,1)としておいて， 固有値0に対する固有ベクトルを順次 (1,-1,0,0,0,0,0,...,0) (1,1,-2,0,0,0,0,...,0) (1,1,1,-3,0,0,0,...,0) (1,1,1,1,-4,0,0,...,0) ... (1,1,1,1,1,1,1,...,1,-(n-1)) のように選べば，これらはすべて互いに直交します． 最後にこれらを正規化すればいいでしょう．

＊ちょっと修正しました．

Re: ｎ×ｎ行列の対角化

mNeji さんのレス (2009/01/23(Fri) 10:40)

固有ヴェクタを少し検討しました．n=2,3 について具体的に求めて遊んでいたら，図形的な漸化式みたいなのが出来たので書いて見ます． ヴェクタの記法はanonさんのそれに準じました．

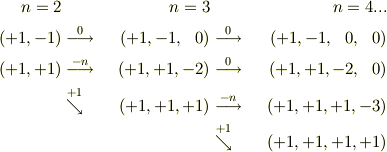
n=2 & &n=3 & &n=4...\\(+1,-1) & \stackrel{0}{\longrightarrow} & (+1,-1,\ \ 0) & \stackrel{0} {\longrightarrow} & (+1,-1,\ \ 0,\ \ 0)\\(+1,+1) & \stackrel{-n}{\longrightarrow} &(+1,+1,-2) & \stackrel{0}{\longrightarrow} & (+1,+1,-2,\ \ 0)\\& \stackrel{+1}{\searrow} &(+1,+1,+1) & \stackrel{-n}{\longrightarrow} &(+1,+1,+1,-3) \\& & & \stackrel{+1}{\searrow} &(+1,+1,+1,+1)

もちろん，anonさんと同じ事を書いているだけですが...．

Re: ｎ×ｎ行列の対角化

toorisugari no Hiro さんのレス (2009/01/23(Fri) 18:56)

> 物理的にはどんな場合に応用出来るのでしょうか？

この行列を 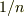1/n 倍したものは，1次元部分空間への射影演算子になりますね．射影演算子は量子力学などで純粋状態を取り出す操作に現れます．

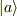n 次元空間の任意の単位ベクトルを |a\rangle とすれば，このベクトルが張る部分空間への射影演算子 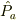\hat P_a は

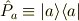
\hat P_a \equiv |a\rangle\langle a|

で与えられます．自明な関係式

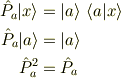
\hat P_a |x\rangle &= |a\rangle~ \langle a|x\rangle\\\hat P_a |a\rangle &= |a\rangle\\\hat P_a^2 &= \hat P_a

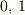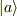から，固有値は 0,\,1 であること， 0 固有ベクトルの張る部分空間は |a\rangle に垂直で原点を通る(超)平面 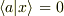\langle a|x\rangle=0 になること，よって，部分空間の次元が 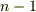n-1 になること，は明らかですね．

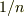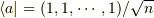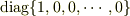今回の行列(の 1/n 倍)は， \langle a| = (1,1,\cdots,1)/\sqrt{n} の場合に対応しますが，計算問題のための形に過ぎないと思います．強いて意味づけすれば，(離散的な物理空間において，)位置の0固有ベクトルが張る部分空間への射影演算子を，運動量空間において表現したもの，という解釈はできます． つまり， \mathrm{diag}\{1,0,0,\cdots,0\} という行列を(離散)フーリエ変換したものですね．

Re: ｎ×ｎ行列の対角化

mNeji さんのレス (2009/01/23(Fri) 20:46)

＞この行列を 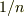1/n 倍したものは，1次元部分空間への射影演算子になりますね．量子力学などで純粋状態を取り出す演算などに現れます．

ご丁寧な解説，有り難うございました．少しは判る気がしてきました．本当に納得出来る事かはまだ判りません...．