ばねの回転座標での問題ですが・・・

UgN さんの書込 (2009/01/18(Sun) 13:38)

こんにちはどうしても最後まで解けないので助けてください

「水平面上で点Oを中心として一定の角速度ωで回転する管の中に，点Oで片側を固定したばね（自然長L，ばね定数k）があって，ばねのもう片側には質量mの質点がついています．」という問題です．x=Lで質点を固定したまま管を回転させ，t=0で質点を放したときの時刻tでの座標x(t)を求めたいのですが，運動方程式は

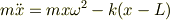
$m\ddot x = mx\omega^2-k(x-L)$

とまでは自分で出せたのですが，微分方程式を解こうとして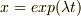， $x=exp(\lambda t)$ を代入すると，うまく 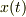x(t) を導くことができません．分かる方，教えてください．おねがいします．

Re: ばねの回転座標での問題ですが・・・

mNeji さんのレス (2009/01/18(Sun) 18:50)

UgNさん，初めまして．

ちょっと毛色の違う問題で面白そうですが，直ぐには解けませんね．

運動方程式をmで割って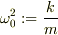， $\omega_0^2 := \frac{k}{m}$ とすると，

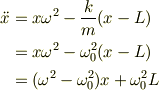
$\ddot x&= x\omega^2-\frac{k}{m}(x-L)\\&= x\omega^2 - \omega_0^2(x-L)\\&=(\omega^2 -\omega_0^2)x +\omega_0^2 L$

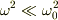いま， $\omega^2 \ll \omega_0^2$ と小さければ，Lを中心とした普通の単振動の式になると思われます．

他方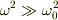， $\omega^2 \gg \omega_0^2$ と大きければ，遠心力が一方的に大きく成って，バネを引き延ばしてしまい，振動する余裕が無くなって静的な平衡に達すると思われます．そのときの変位 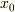x_0 とすると

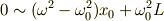
$0 \sim (\omega^2 -\omega_0^2)x_0 +\omega_0^2 L$

となります．

そこで，新たな変数 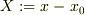X := x -x_0 として，運動方程式を書き直すと

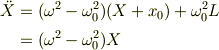
$\ddot X&=(\omega^2 -\omega_0^2)(X+x_0) +\omega_0^2 L\\&= (\omega^2 -\omega_0^2)X$

となるので，なんとか？

Re: ばねの回転座標での問題ですが・・・

ミュフ猫さんのレス (2009/01/19(Mon) 08:00)

数学の専門書によれば，

dx/dt = v

として，

dv/dt = v・(dv/dx)

を利用し，変数分離形に持ち込めばよいそうです．最終的に，

t = f(x)

の形になるようですが，ここから，初等的に逆関数が求まるかは不明．ｗ

Re: ばねの回転座標での問題ですが・・・

toorisugari no Hiro さんのレス (2009/01/19(Mon) 14:47)

$m\ddot x = mx\omega^2-k(x-L)$ は非同次線形常微分方程式と呼ばれるものです．今回の問題は，非同次項は定数ですから，mNejiさんの書かれたように，シフトすれば同次線形常微分方程式にできる比較的簡単な問題です．

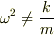$\omega^2 \ne \frac{k}{m}$ となる場合を考えると

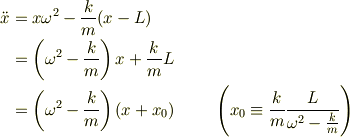
$\ddot x &= x\omega^2-\frac{k}{m}(x-L)\\&= \left(\omega^2-\frac{k}{m}\right)x+\frac{k}{m}L\\&= \left(\omega^2-\frac{k}{m}\right)(x+x_0) & \left(x_0 \equiv \frac{k}{m}\frac{L}{\omega^2-\frac{k}{m}}\right)$

となり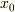， x_0 は定数なので方程式は

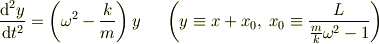
$\frac{\mathrm{d}^2 y}{\mathrm{d} t^2} &= \left(\omega^2-\frac{k}{m}\right)y& \left(y\equiv x+x_0,~ x_0 \equiv \frac{L}{\frac{m}{k}\omega^2-1}\right)$

と変形でき，係数 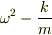$\omega^2 - \frac{k}{m}$ の正負で場合分けすれば解けますね．

係数 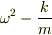$\omega^2 - \frac{k}{m}$ が0になる場合は上式の解は発散しますが，変形せずに，直接，元の方程式を積分すれば正しい解が出てきます．

Re: ばねの回転座標での問題ですが・・・

UgN さんのレス (2009/01/20(Tue) 08:49)

みなさん，大変わかりやすい解説ありがとうございました．

うまく式変形すればずいぶん解きやすくなりますね．自分でも，もう一度考えて，非同次微分方程式の一般解を求める方法でx(t)を出してみたのですが，それとmNejiさんやtoorisugari no Hiroさんのいわれた同次微分方程式から求めた解が一致したので良かったです．

でも，おふたりのように式変形したほうが，スマートに解けました

すごく助かりました

Re: ばねの回転座標での問題ですが・・・

mNeji さんのレス (2009/01/20(Tue) 08:57)

＞自分でも，もう一度考えて，非同次微分方程式の一般解を求める方法でx(t)を出してみたのですが，

素晴らしいですね．若し宜しければ，その解法をお書き下さると善いかも知れませんね．

[home] [掲示板] [ページの先頭]