局所慣性系が選べることの証明
局所慣性系が選べることの証明
ファイル さんの書込 (2009/01/13(Tue) 04:54)
教科書で分からないところがあったので,宜しくお願いします.
四次元リーマン多様体が局所的に平坦であることを証明する,というものなのですが
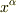 を任意の座標系,ダッシュのついた
を任意の座標系,ダッシュのついた 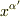 を求めたい座標系(つまり局所慣性系)とします.
変換行列Λを点P(座標は
を求めたい座標系(つまり局所慣性系)とします.
変換行列Λを点P(座標は 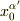 )で展開すると
)で展開すると
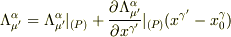 同様に計量も展開
同様に計量も展開
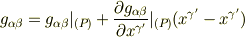
これを座標変換した計量成分の式
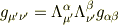
に代入すると
](http://hooktail.maxwell.jp/bbslog/39a27bf1ea59bd7e527454db392c0dcf.png)
となります.ここまでの計算は自分でも追うことができました.
その後なのですが
P点で局所慣性系になるために
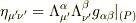 (1)式とします.
(1)式とします.
が成り立たなくてはいけなくて,本には「これは10個の方程式で,これを満たすのにΛに現れる16個の任意の定数が使える.」と記述されています.
これは,適当なΛの成分を選ぶことによって,(1)式が成り立つようにすることが出来る.と理解しました.
次に,
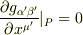 (2)式とします.
(2)式とします.
という40本の式が成り立たなくてはいけなくて,「Λという行列を考えるとき,40個の 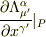 を上手く選んで,(2)式とするように点Pの近傍で座標を決めるやり方はただ一通り可能である.」と記述されているのですが
なぜ,急に
を上手く選んで,(2)式とするように点Pの近傍で座標を決めるやり方はただ一通り可能である.」と記述されているのですが
なぜ,急に 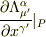 が出てきたのかが分からないです.
テイラー展開した
が出てきたのかが分からないです.
テイラー展開した 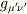 はどこで使うのでしょうか?
はどこで使うのでしょうか?
Re: 局所慣性系が選べることの証明
yama さんのレス (2009/01/13(Tue) 23:31)
たぶん次のようなことだと思います.
式が煩雑になるので添字を省略して表します.
座標変換して得られた局所慣性系の計量テンソルは次のように 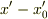 で展開されます.
で展開されます.
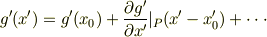
これが局所慣性系である条件としては,点P(すなわち 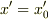 )で
)で 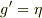 であること,従って
であること,従って 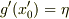 が成り立たねばならないのは当然ですが,それだけでなくPの近傍でも
が成り立たねばならないのは当然ですが,それだけでなくPの近傍でも 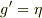 からのずれが微小でないといけません.
そのためには,
からのずれが微小でないといけません.
そのためには, 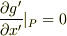 も成り立つ必要があります.
も成り立つ必要があります.
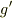 は
は  を
を 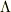 で変換したものなので,
で変換したものなので, 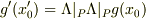 となります.その場合,
となります.その場合, 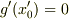 は,
は, 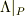 についての10個の連立方程式になりますが,
についての10個の連立方程式になりますが, 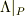 の値を適当に選べば,この連立方程式を満たすことができます.
「Λに現れる16個の任意の定数」というのは,この,
の値を適当に選べば,この連立方程式を満たすことができます.
「Λに現れる16個の任意の定数」というのは,この, 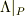 のことでしょう.なお,Λには任意性があるので16個の値は一意的には決まりません.
のことでしょう.なお,Λには任意性があるので16個の値は一意的には決まりません.
次に,  や
や 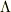 を
を 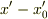 の1次の項まで展開すると,
の1次の項まで展開すると, 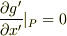 は,
は, 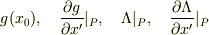 からなる40個の式になります.すなわち,ファイルさんが導かれた
からなる40個の式になります.すなわち,ファイルさんが導かれた 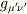 の展開式の1次の係数を0と置いた式です.
従って,40個の
の展開式の1次の係数を0と置いた式です.
従って,40個の 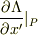 の値を上手く選べば,この式が満たされることになります.
の値を上手く選べば,この式が満たされることになります.
Re: 局所慣性系が選べることの証明
ファイル さんのレス (2009/01/14(Wed) 03:08)
ありがとうございます.
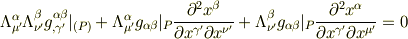
を成り立たせるような,
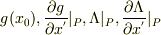 を選ぶ,ということだと思いますが
を選ぶ,ということだと思いますが

を選んで,式を満たすようにするというのは分かるのですが
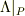 は,
は, 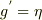 という式を満たさせるためにもう選んでしまったのではないのですか?
とすると,その微分である
という式を満たさせるためにもう選んでしまったのではないのですか?
とすると,その微分である 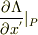 はもうすでに決定されていて,自由に選ぶことが出来ないように思えるのですが・・・.
すみません,もう少し詳しくお願いします.
はもうすでに決定されていて,自由に選ぶことが出来ないように思えるのですが・・・.
すみません,もう少し詳しくお願いします.
Re: 局所慣性系が選べることの証明
ファイル さんのレス (2009/01/16(Fri) 19:11)
基本的なところが,あまり理解できてないかもしれません.
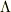 というのは,ちゃんと書くと
というのは,ちゃんと書くと 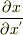 ですが,ある値
ですが,ある値 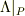 というのは,
Pでの座標に対して,関数
というのは,
Pでの座標に対して,関数 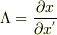 が返す値というよりは
P点での計量の値
が返す値というよりは
P点での計量の値 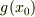 を,
を, 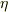 に変換するような行列要素の値
と考えて良いのでしょうか?
に変換するような行列要素の値
と考えて良いのでしょうか?
この問題を具体的に考えて,計算することは難しいでしょうか?
自分で,三次元空間にある半径1の球の例を考えてみたのですが(この球面上は曲がった空間ですよね?)
計量 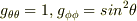 になると思うんですけど,
になると思うんですけど, 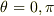 の点では,どうやってもユークリッド計量にならずにおかしなことになってしまいます.
の点では,どうやってもユークリッド計量にならずにおかしなことになってしまいます.
Re: 局所慣性系が選べることの証明
toorisugari no Hiro さんのレス (2009/01/16(Fri) 20:10)
> 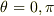 の点では,どうやってもユークリッド計量にならずにおかしなことになってしまいます.
の点では,どうやってもユークリッド計量にならずにおかしなことになってしまいます.
普通,座標関数は一つである必要はなく,重なり合うように複数定義します.南極と北極は自転軸を軸とする極座標系の特異点なので,別の座標系(自転軸以外を軸とする極座標系)で表示するだけです.
Re: 局所慣性系が選べることの証明
ファイル さんのレス (2009/01/16(Fri) 21:44)
ありがとうございます.
特異点について詳しいことは知らないので,別の点, 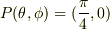 で考えてみます.
その点での計量は
で考えてみます.
その点での計量は
![g_{\mu\nu}=\left[ \begin{array}{ccc}1&0 \\0&\frac{1}{2} \\\end{array} \right]](http://hooktail.maxwell.jp/bbslog/04a992c66e29f77f80918f4e62229f8d.png)
となります.この行列をユーグリッド行列にする変換行列は
![\left[ \begin{array}{ccc}1&0\\0&\sqrt{2}\\\end{array} \right]](http://hooktail.maxwell.jp/bbslog/2ad3cd996a2aea48306304818d4358c0.png)
になると思います.
記事 No.22740の質問というのは, 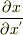 を計算して(今の場合なら,
を計算して(今の場合なら,  を
を  で微分するなど.)求められた式に,Pの値を代入する.ということをせずに,
上の行列を見つけたように,Pでの計量をミンコフスキー計量に(今の場合はユークリッドですが)変換する適当な行列を見つければ良いのだろうか?という意味です.
(両方計算して一致すれば良いのでしょうが,前者の計算をしたら少しおかしなことになってしまいました.)
で微分するなど.)求められた式に,Pの値を代入する.ということをせずに,
上の行列を見つけたように,Pでの計量をミンコフスキー計量に(今の場合はユークリッドですが)変換する適当な行列を見つければ良いのだろうか?という意味です.
(両方計算して一致すれば良いのでしょうが,前者の計算をしたら少しおかしなことになってしまいました.)
つまり, 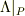 とは
とは
![\left[ \begin{array}{ccc}1&0\\0&\sqrt{2}\\\end{array} \right]](http://hooktail.maxwell.jp/bbslog/2ad3cd996a2aea48306304818d4358c0.png)
のこと,で合っていますでしょうか?
Re: 局所慣性系が選べることの証明
yama さんのレス (2009/01/17(Sat) 00:15)
その変換行列は正しくないように思います.
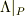 は
は
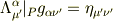
ではなく
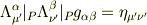
を満たすことが必要です.
なお, 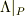 を求めるために
を求めるために 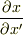 を計算する必要はありません.ファイルさんが述べられているように,P点での計量
を計算する必要はありません.ファイルさんが述べられているように,P点での計量 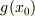 の値を,
の値を, 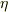 に変換するような行列要素の値と考えればいいわけです.
そもそも
に変換するような行列要素の値と考えればいいわけです.
そもそも 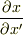 を計算するには,
を計算するには,  と
と 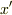 の関係が分かっていなければいけませんが,初めから分かっているわけではなく,それを求めるのが問題だからです.
の関係が分かっていなければいけませんが,初めから分かっているわけではなく,それを求めるのが問題だからです.
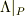 が決まれば,P点での計量が
が決まれば,P点での計量が 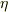 になるわけですが,P点の近傍においても
になるわけですが,P点の近傍においても 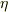 との差が微小になるようにしないといけません.そのために
との差が微小になるようにしないといけません.そのために 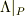 に
に 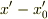 について1次の項を付け加えて
について1次の項を付け加えて  の展開式の1次の項が0になるようににするわけです.
の展開式の1次の項が0になるようににするわけです.
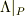 に加える1次の項の係数が
に加える1次の項の係数が 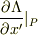 ですが,これも定数と考えて求めればよいのであって,
ですが,これも定数と考えて求めればよいのであって, 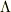 を求めて微分する必要はありません.
を求めて微分する必要はありません.
Re: 局所慣性系が選べることの証明
ファイル さんのレス (2009/01/17(Sat) 01:40)
>を満たすことが必要です.
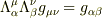 を行列表示すると,
を行列表示すると, 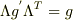 ですから,
ですから,
![\left[ \begin{array}{ccc}1 & 0\\ 0&\sqrt{2}\\\end{array} \right] \left[ \begin{array}{ccc}1 & 0\\ 0&\frac{1}{2}\\\end{array} \right]\left[ \begin{array}{ccc}1 & 0\\ 0&\sqrt{2}\\\end{array} \right]=\left[ \begin{array}{ccc}1 & 0 \\ 0&1\\\end{array} \right]](http://hooktail.maxwell.jp/bbslog/d196fa7268f24d56e4b9d38b3f2d33fc.png)
となりませんか?
>  と
と 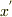 の関係が分かっていなければいけませんが,初めから分かっているわけではなく,それを求めるのが問題だからです.
の関係が分かっていなければいけませんが,初めから分かっているわけではなく,それを求めるのが問題だからです.
なるほど!確かにそうですね. もやもやしていたものが晴れました.
それでは,
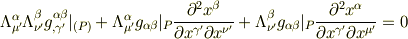
という式は, 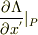 以外は全て決定された何かの数字ですから,40コの
以外は全て決定された何かの数字ですから,40コの 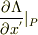 に関する,40本の連立方程式になる.(だから解ける.)ということでしょうか.
これが冒頭の「40個の
に関する,40本の連立方程式になる.(だから解ける.)ということでしょうか.
これが冒頭の「40個の 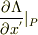 を上手く選んで,(2)式とするように点Pの近傍で座標を決めるやり方はただ一通り可能である.」の意味ですね?
を上手く選んで,(2)式とするように点Pの近傍で座標を決めるやり方はただ一通り可能である.」の意味ですね?
Re: 局所慣性系が選べることの証明
yama さんのレス (2009/01/17(Sat) 08:53)
ちょっと勘違いしていましたが,変換行列はファイルさんが求められたもので合っていると思います. その他についてもファイルさんが理解されている通りだと思います.
Re: 局所慣性系が選べることの証明
ファイル さんのレス (2009/01/17(Sat) 10:57)
ありがとうございました! お二人のおかげで,悩みが解決しました.
ところで,申し訳ないのですがもう一つ質問してもよろしいでしょうか?
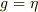 が一次まで成り立っていること,というのは局所的に慣性系が選べるということ,つまり等価原理の表現になっていると思います.
一般相対性理論は通常,相対性原理と等価原理の二つを原理として展開されているものと思いますが,いままでの話から分かるように,リーマン多様体では局所的に
が一次まで成り立っていること,というのは局所的に慣性系が選べるということ,つまり等価原理の表現になっていると思います.
一般相対性理論は通常,相対性原理と等価原理の二つを原理として展開されているものと思いますが,いままでの話から分かるように,リーマン多様体では局所的に 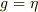 が成り立つということが証明できたので,等価原理は「原理」ではないのでは?と思うのですが,どうでしょうか?
(それとも,時空が四次元リーマン多様体である.ということが等価原理に対応するのでしょうか.)
が成り立つということが証明できたので,等価原理は「原理」ではないのでは?と思うのですが,どうでしょうか?
(それとも,時空が四次元リーマン多様体である.ということが等価原理に対応するのでしょうか.)
Re: 局所慣性系が選べることの証明
yama さんのレス (2009/01/17(Sat) 12:34)
>それとも,時空が四次元リーマン多様体である.ということが等価原理に対応するのでしょうか.
そのように考えてよいと思います. 等価原理は,一般相対論を定式化するための指針であったと思います. 局所慣性系の存在という物理的な要請を,局所的なミンコフスキー計量の存在の要請と考えることによって,重力理論がリーマン多様体を用いて幾何学的に定式化されたわけです. 一般相対論の完成後は,等価原理はリーマン多様体の理論に包含されていると考えるのが妥当でしょう.