電荷と電場

eKinetic さんの書込 (2009/01/03(Sat) 20:43)

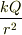半径の導体球面上に正の全電荷が均等に分布しています．全電荷を点電荷の集まりとみれば，その一つの点電荷aが作る電場は，点電荷aのきわめて近くで，無限大の大きさになります．残りの点電荷が，aの位置に作る電場も，正となるはずですから，半径の球面上近くの電場は，無限大の大きさになるように思います．しかし，実際の電場は，点電荷aの近くで，ガウスの法則によって， $\frac{kQ}{r^2}$ となり，無限大にはなりません．

はじめの考え方のどこに，間違いがあるのでしょうか？

点電荷aの作る電場が等方的でない（導体球の内部方向は電場ゼロである）ところにヒントがあるような気がするのですが，納得いく説明ができません...

Re: 電荷と電場

mNeji さんのレス (2009/01/03(Sat) 21:47)

数学的に厳密な理解が出来ている訳ではありませんが，＞全電荷を点電荷の集まりと見るのがに違和感を持ちます．

そもそも電子すら点電荷と考え難い様に思いますし...．やはり，素直に，＞全電荷が均等に分布この観点に立つ方が自然な解釈と思います．

本当の所はどうなんでしょうかねえ．

Re: 電荷と電場

yama さんのレス (2009/01/03(Sat) 22:14)

点電荷が0でない有限の電荷を持つ場合は，点電荷による電場は点電荷の無限小近傍で無限大になります．しかし，点電荷の電荷が無限小の場合は，電場は無限大にはなりません．球面上の電荷を点電荷の集まりと見なすときは，各点電荷の電荷は無限小になります．なぜなら，もし各点電荷が0でない有限の電荷を持つならば，球面上の全電荷が無限大になるからです．

Re: 電荷と電場

Yokkun さんのレス (2009/01/04(Sun) 02:00)

yamaさんの説明につきる問題ですが，補足を．

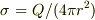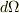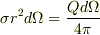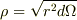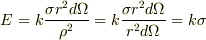もし，球面上の面電荷密度を $\sigma=Q/(4\pi r^2)$ とすると中心からの立体角 $d\Omega$ に含まれる電荷は， $\sigma r^2d\Omega = \frac{Qd\Omega}{4\pi}$ となります．一方，この微小部分の電荷を点電荷とみなせるのは，せいぜい $\rho=\sqrt{r^2d\Omega}$ 以上の距離においてのみ可能であると思われます．この最小距離において微小部分を点電荷に近似した場合の電場は， $E=k\frac{\sigma r^2 d\Omega}{\rho^2}=k\frac{\sigma r^2d\Omega}{r^2d\Omega}=k\sigma$ となり，有限です．

以上は，電荷分布をあくまでも連続と考えた場合の考察です．現実の帯電体で原子の大きさのレベルまで降りれば，電荷の偏在が無視できなくなりますが，そうなれば今度は量子力学的な考察が必要になるでしょう．自然は巧妙な手口で無限大の矛盾をすりぬけているかのように思えます．

Re: 電荷と電場

eKinetic さんのレス (2009/01/04(Sun) 10:46)

みなさん，お返事ありがとうございます．

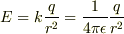点電荷からの距離を改めてとおくと，その位置の電場は， $E=k\frac{q}{r^2}=\frac{1}{4\pi\epsilon}\frac{q}{r^2}$ ここで，分母のが無限小でも，分子のも無限小になるので，は，有限になる．ということですね．

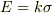
Yokkunさん， > $E=k\sigma$

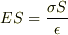
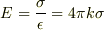ですが，球表面近くで，導体内部と外部にわたる円柱の閉曲面を作ってガウスの法則を適用すると，円柱が球表面を切る面積をとして， $ES=\frac{\sigma S}{\epsilon}$ $E=\frac{\sigma}{\epsilon}=4\pi k\sigma$ となるように思いますが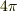， $4\pi$ だけ合いません．再度，ご指摘いただけると幸いです．

Re: 電荷と電場

Yokkun さんのレス (2009/01/04(Sun) 11:28)

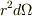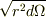私のやった見積もりは，微小面積 $r^2d\Omega$ がもつ電荷を点電荷扱いするには，オーダーとして概ね $\sqrt{r^2d\Omega}$ 以上離れた距離において可能であろうという大雑把な見積もりであり，なおかつ球面の他の部分を無視しているわけですから，合わないのは当然です．ここではおおまかな見積もりとして，無限小/無限小＝有限を示すにとどめました．重要なのは分母と分子の「無限小」の度合いが同じであることですね？

Re: 電荷と電場

eKinetic さんのレス (2009/01/04(Sun) 12:07)

>重要なのは分母と分子の「無限小」の度合いが同じであることですね

よくわかりました．

mNejiさん，yamaさん，そしてYokkunさん

示唆に富むご教示をいただき，ありがとうございました．すごくスッキリしました．感謝申し上げます．

[home] [掲示板] [ページの先頭]