円運動における加速度の疑問
円運動における加速度の疑問
army さんの書込 (2008/12/31(Wed) 22:18)
ある本に書いてあった文を引用します.
「・・・・そして円軌道の内側を向くような移動方向の修正をもたらしているものが,この物体に発生している加速度であり,その発生源が向心力である. なお,遠心力はこのとき向心力と同じ大きさで反対向きに発生しおり,合力としては完全に打ち消しあっているが,加速度は残る.「合力0なのに加速度がある?」というのは不可解にも思えるが,それが「円運動」というものの特殊な性質であると,この場では説明しておく.・・・・」
この文章の「なお,遠心力はこのとき向心力と同じ大きさで反対向きに発生しおり,合力としては完全に打ち消しあっているが,加速度は残る」 が気になり,ずっと悩んでいます. どういうことなのか説明していただけませんか.お願いします.
Re: 円運動における加速度の疑問
Yokkun さんのレス (2008/12/31(Wed) 22:58)
>円軌道の内側を向くような移動方向の修正をもたらしているものが,この物体に発生している加速度であり,その発生源が向心力である.
これが慣性系から見た立場です.
>遠心力はこのとき向心力と同じ大きさで反対向きに発生しおり,合力としては完全に打ち消しあっているが
これがともに動く加速系の立場.
>加速度は残る
打ち消しあうのに加速度は残る・・・というのはおかしいですね?この表現は間違いだと思います. 加速系の立場に立てば,加速度はありません.代わりに慣性力である遠心力と向心力がつりあっていると見るわけです.式で書けば,
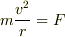
慣性系の立場は,左辺を運動方程式の左辺と見ます.加速系の立場は左辺を向心力  とつりあう遠心力と見るわけです.
とつりあう遠心力と見るわけです.
Re: 円運動における加速度の疑問
army さんのレス (2009/01/02(Fri) 09:33)
なるほどよく分かりました. ありがとうございました.
Re: 円運動における加速度の疑問
komagatake さんのレス (2009/01/08(Thu) 12:55)
>なお,遠心力はこのとき向心力と同じ大きさで反対向きに発生しおり,合力としては完全に打ち消しあっているが,加速度は残る」
遠心力と向心力は異なる表現系(座標系)での言葉です. 同時に存在する力ではありませんので合力を考えることは出来ません. 大きさが等しくて向きが逆だということを 「合力が完全に打ち消す」と表現して言いわけではありません.
「合力は打ち消すが加速度は残る」というようのも意味不明な文章ですね. 力と加速度を結びつける運動方程式の立場と矛盾する表現が使われているのですから.
Re: 円運動における加速度の疑問
toorisugari no Hiro さんのレス (2009/01/08(Thu) 14:57)
komagatakeさん
> 遠心力と向心力は異なる表現系(座標系)での言葉です.
typoと思いますが, 遠心力と向心加速度ですよね.
定義にもよりますが,向心力を 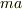 でなく,加速度を起こす力の意味で使うのなら,例えばおもりを回転させる紐の張力の様に,実在の力ですからどの座標系でも使えるので,遠心力と比較しても,向心加速度と比較しても良いですよね.
でなく,加速度を起こす力の意味で使うのなら,例えばおもりを回転させる紐の張力の様に,実在の力ですからどの座標系でも使えるので,遠心力と比較しても,向心加速度と比較しても良いですよね.
# 「ある本」はゴミ箱行きですね.
Re: 円運動における加速度の疑問
anon さんのレス (2009/01/09(Fri) 09:33)
> # 「ある本」はゴミ箱行きですね. この記述,ウェブ上にあるようですね. http://www5d.biglobe.ne.jp/~owhari/panekit/panekit_cornroter.htm
Re: 円運動における加速度の疑問
komagatake さんのレス (2009/01/09(Fri) 19:26)
私は向心力は円運動における向心加速度に対応する力だと考えています.方向が変わることによって生じる加速度の存在を強調して代名詞的に呼んでいるのです.F=maの左辺が向心力であるとは考えていません.円運動の種類によって向心力として働く力が色々あるということです.張力の場合も,抗力の場合も,摩擦の場合もあります.万有引力の場合もあります.それぞれの力がそれぞれの場面で向心力として働いたということです.
円運動だから違いがハッキリしないのです.どう解釈してもいいという議論が出てくるのです. 万有引力=向心力と言ってしまえばr=一定でない運動で混乱が生じます. r方向の加速度は Ar=d^2r/dt^2−r(dθ/dt)^2 です. r方向の力は Fr=mAr です.この場合でも中心向きにmr(dθ/dt)^2の力が働いています.これを向心力と呼ぶことは可能です.md^2r/dt^2の部分を含めて向心力と呼ぶことはないと思っています.万有引力はFrですから万有引力=向心力ではありません.
Re: 円運動における加速度の疑問
toorisugari no Hiro さんのレス (2009/01/10(Sat) 18:00)
> 私は向心力は円運動における向心加速度に対応する力だと考えています. > 万有引力=向心力と言ってしまえばr=一定でない運動で混乱が生ます.
円運動ではないときの「向心加速度」および「向心力」の定義は何ですか? それは「加速度,力」の,動径成分,あるいは速度に直交する成分とは違うのですか?
原点の近傍を「力を受けないで」慣性運動(=等速直線運動)で通過する物体の加速度の動径成分
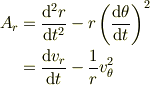
の値はもちろん0ですが,各項は非零です. # 加速度の動径成分だけでなく速度に直交する成分の値ももちろん0です.
このときも 「中心向きにmr(dθ/dt)^2の力が働いています.これを向心力と呼ぶことは可能です.」 とおっしゃるのですか?
見かけの力と力を混同されているように思えます.
もし,そうでなく,運動を「向心加速度」を持つ成分と持たない成分でわけるという考え方をされているのなら,その考え方および有用性が書かれている文献を教えてください. # きっと「向心加速度」の,加速度の動径成分あるいは速度に直交する成分と異なる,かつ,座標系に依存しない(ベクトルで記述された),定義も書かれているはずですよね.
そもそも
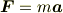
の右辺 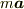 は慣性系においては力
は慣性系においては力 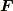 と「同値」ですが,
と「同値」ですが, 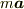 はあくまでも「質量×加速度」であって力と「同義」ではありません.
# 任意の観測者に対して
はあくまでも「質量×加速度」であって力と「同義」ではありません.
# 任意の観測者に対して 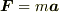 が成り立つのなら,「同義」と考えてもいいかもしれませんが,違いますね.
が成り立つのなら,「同義」と考えてもいいかもしれませんが,違いますね.
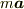 を,見かけの力ならまだしも,力と呼ぶ事には賛成できません.
を,見かけの力ならまだしも,力と呼ぶ事には賛成できません.