BEC
BEC
けん(大学3年) さんの書込 (2008/12/27(Sat) 23:09)
理想ボース気体,3次元,T<Tcでなぜμ=0なのかという質問です.
理想ボース気体,3次元を考えます. 温度Tのとき,全粒子数をN,エネルギーε=0の粒子数をN0,それ以外(ε≠0)の粒子数をN'とします.N=N0+N'です. 化学ポテンシャルμ=0かつN=N'なる温度があり,これをTcとおきます. ところでN'には最大値N'maxがあり,μ=0のときN'=N'maxとなります. つまり,温度を高温から下げていったとき,TcになったときにN=N'=N'maxとなります.そして,さらに温度を下げたとき,N>N'maxであるため,N0が増え始めます.つまり,ボースアインシュタイン凝縮が始まります.
ここまではどのテキストにも書かれている事柄です. しかし,T<Tcでμ=0であり続けることに関して疑問を持っています. 何冊ものテキストにあたってみて,
1.「T<TcではN0がマクロな量になるので,そのためにはN0=1/(exp(-μ/kT)-1)から,μが0でなければならないkはボルツマン定数」 という説明があったのですが,T=Tcでミクロな数だと考えられるN0がT<TcなるTの中でも,特にTcより少し低い温度でもNのオーダーになるという根拠は何なのでしょうか. 絶対零度より少し高い温度ではN0=O(N)なのでしょうけれど.
2.「T<TcでN'はN'maxになり(→μ=0となる),それより低い温度ではN'に入りきらない粒子はN0に入る.」という説明があったのですが,T<TcでN'はN'maxになることの根拠は何なのでしょうか.温度を下げるのだから,N'=N'maxとならずに,エネルギーε=0であるN0に入っていくという可能性もあります.
T<Tcでμ=0になることを数式で示す方法があればその方法もしくはそれが載っているテキストを教えて頂きたいです. よろしくお願いします.
Re: BEC
nomercy さんのレス (2008/12/28(Sun) 05:06)
もっともな疑問ですね.
まず,T=Tcでは密度ρ0(ρ0≡N0/体積)は零で,これより温度を下げると連続的に大きくなっていきます.もちろん,T=Tcでも連続です. なぜ Tc より少しだけ低い温度でも非零かというと,2.に書いてあるのがその一つの説明です. すなわち,T < Tc では必ず ρ' < ρ だからです.
さて,本題の化学ポテンシャルですが,これは1.に書いてある考察の通りです. (この説明はかなり大まかなものですが) つまり,(V e^{-μ/T}-1)^(-1) V:体積が体積が十分大きい極限で有限の値を持つには化学ポテンシャルが非常に小さく(-μ/T ∝ V^(-1) << 1)なければならない.
以上に書いた説明はけんさんの質問文を書き直しただけのようなものなので,これだけ読んでも釈然としないかと思います. 具体的に化学ポテンシャルを評価しているテキストとして,例えば 田崎晴明「統計力学」培風館 新物理学シリーズ があります.参考にしてみて下さい.
Re: BEC
けん(大学3年) さんのレス (2008/12/31(Wed) 00:24)
>nomercyさん
コメントありがとうございます. 田崎晴明「統計力学」培風館 新物理学シリーズ は見てみましたが,このテキストでは,T<Tcでμ=0であるとしとよいと言ってしまうことによってμ=0でのN'を求め(つまりN'=N'maxとしてしまう),このN'を用いてμの振る舞いを見ています.議論は確かに無矛盾ではありますが,はじめにμ=0としてしまうことの根拠がないように思います.
はじめにμ=0としてしまうことの根拠を知りたいです. 解析的に示せるのでしょうか.
Re: BEC
yama さんのレス (2008/12/31(Wed) 11:18)
ランダウ-リフシッツ「統計物理学」の§62の説明が参考になると思います.
Re: BEC
nomercy さんのレス (2009/01/01(Thu) 03:25)
T < Tc で μ=0 となるのは No.22597 で理解できるのではないでしょうか. つまり T < Tc では ρ' ≦ ρ'max < ρ なので必ず ρ' < ρ であり,ρ0 ≠ 0 となる.一方,ρ0 ≠ 0 となるには μ = 0 でなければならない.従って T<Tc では μ=0. 逆に,T > Tc では,μ≠0でなければならない.なぜなら,仮にμ=0とすると ρ'=ρ'max > N となり,矛盾するからである.
Re: BEC
けん(大学3年) さんのレス (2009/01/02(Fri) 00:45)
コメントありがとうございます.
>yamaさん ランダウ-リフシッツは読んでみたのですが,T<Tcでμ=0であるとしとよいことの根拠が不明確だと感じていました. T=Tcではμは0ですが,T<Tcで再び小さくなる(絶対値は大きくなる)可能性を捨て切れていないと思います.
>nomercyさん >ρ0 ≠ 0 となるには μ = 0 でなければならない. 有限温度なので,μ=0でなければならないとはいえないのではないでしょうか. T=0ではμ=0でなければなりませんが.
Re: BEC
nomercy さんのレス (2009/01/02(Fri) 01:12)
μ ∝1/V → 0 でないと ρ0 が有限に残らないのでは?
Re: BEC
けん(大学3年) さんのレス (2009/01/02(Fri) 02:05)
μ ∝1/Vはどこから出てくるのでしょうか.
Re: BEC
nomercy さんのレス (2009/01/02(Fri) 02:18)
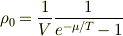
なので,これが体積無限大で有限に残るには,ボーズ因子が体積に比例しなければならない.化学ポテンシャルの体積依存性を
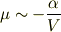
とすると
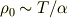
となり,有限になる.化学ポテンシャルの体積依存性の指数がこれより小さいとρ0 → 0となる.
というように,ρ0が非零になるには化学ポテンシャルが零になることが必要.
Re: BEC
けん(大学3年) さんのレス (2009/01/02(Fri) 02:47)
ρ0=N0/Vなので,N0が有限である以上,V→∞でρ0→0となっても構わないと思うのですが.
Vを∞にする極限を考えるという考え方は初めて見ました.これはよくあることなのでしょうか.よく使われるテキストがあれば教えて頂けないでしょうか.V→∞とするときに何を変数と見ているのかについて僕が分かっていない恐れがありますので.
Re: BEC
nomercy さんのレス (2009/01/02(Fri) 03:03)
T < Tc では ρ' ≦ ρ'max < ρ なので必ず ρ' < ρ であり,ρ0 ≠ 0 となるのでは?
熱力学極限(密度を一定にして体積と粒子数を無限大)においても残るのが本物の秩序であり,相転移です.今,秩序変数はρ0と考えており,秩序相ではこれが非零です.熱力学極限をとらない場合は無秩序相でも非零です. この辺の扱いは田崎さんのテキストに倣っています.