ドップラー効果について計算してみました
ドップラー効果について計算してみました
UP さんの書込 (2008/12/25(Thu) 20:40)
振動数  の光を放つ光源が速度
の光を放つ光源が速度  で観測者に向かっている場合について教えて下さい.
で観測者に向かっている場合について教えて下さい.
ダッシュがついている記号は静止している観測者から見た移動している光源の値です.
光源が 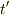 秒間光を放っていたとすると,
光の先端は
秒間光を放っていたとすると,
光の先端は 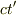 の位置にあり,光の終端は
の位置にあり,光の終端は 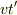 の位置にあるため,光の全長は
の位置にあるため,光の全長は
 になります.
この光が観測者に全て観測されるためには
になります.
この光が観測者に全て観測されるためには
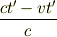
秒かかります.
この中に 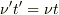 回の振動が入っているわけなので,振動数は
回の振動が入っているわけなので,振動数は
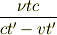
となり, 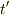 に
に
![\frac{-vx/c^{2}+t}{\sqrt[]{1-v^{2}/c^{2}}}](http://hooktail.maxwell.jp/bbslog/7b0d2ea1f30cb911cb6e37d0923841c7.png)
を代入すると
![\frac{\nu tc \sqrt[]{1-v^{2}/c^{2}}}{(c-v)(-vx/c^{2}+t)}](http://hooktail.maxwell.jp/bbslog/24ba9e19ab3943ea92f104050e6abd80.png)
となりました. 式の中にxとtが出てきたのですが, 場所や光っている時間によって周波数が変わってしまうのでしょうか?
Re: ドップラー効果について計算してみました
Yokkun さんのレス (2008/12/26(Fri) 09:43)
観測者が観測する振動数を,
「光源において観測される光源の座標および固有時と振動数」
で書いたのですから, 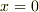 とすべきなのです.
とすべきなのです.
光を出し始めた事象点 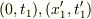 光を出し終えた事象点
光を出し終えた事象点 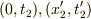 とすると,
とすると,
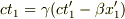
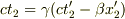 ただし,
ただし, 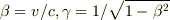
ですから, 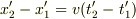 を考慮して,
を考慮して,
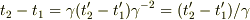
となります.普通は変換式の微分をとって,
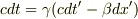
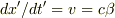 を考慮して,
を考慮して,
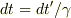 とすると簡明です.結果は,
とすると簡明です.結果は,
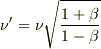 となり,UPさんの式で
となり,UPさんの式で 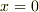 とおいたものと同じです.
ちなみに,光の(縦)ドップラー効果はエネルギーと運動量の4元ベクトルの変換を用いても簡単に導くことができます.
4元運動量ベクトル
とおいたものと同じです.
ちなみに,光の(縦)ドップラー効果はエネルギーと運動量の4元ベクトルの変換を用いても簡単に導くことができます.
4元運動量ベクトル 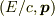 が,
が, 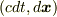 と同じローレンツ変換に従うことから,
と同じローレンツ変換に従うことから,
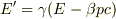 ここで,
ここで, 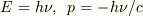 を考慮して,
を考慮して,
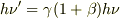 となり,上と同じ結果を得ます.
となり,上と同じ結果を得ます.
Re: ドップラー効果について計算してみました
UP さんのレス (2008/12/28(Sun) 17:14)
なるほど,とても理解できました. ありがとうございました.
一つだけ,わからなかたので,お願いします.
僕の頭の中では,
光を出し始めた事象点 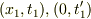 光を出し終えた事象点
光を出し終えた事象点 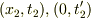 かなぁって思いました.
動いている光源から見ると光を出し始めたところも出し終えたところも原点なのかなって思いました.
かなぁって思いました.
動いている光源から見ると光を出し始めたところも出し終えたところも原点なのかなって思いました.
Re: ドップラー効果について計算してみました
Yokkun さんのレス (2008/12/28(Sun) 19:44)
>ダッシュがついている記号は静止している観測者から見た移動している光源の値です.
と書かれていますね.表現が微妙ですが,式中のあつかいは明らかにダッシュつきが観測者系の座標だと思います.