無題

滑車さんの書込 (2008/12/23(Tue) 17:06)

慣性モーメントＩ，半径Ｒの滑らかに回転する滑車を通して，ひもの一端には質量Ｍのおもりがついて，もう一端にはばね定数Ｋのばねが付けられ，ばねのもう一方は地面に固定されている．おもりをつりあいの位置から長さａだけ引っ張り静かにはなしたとき，単振動するがそれを証明しろ．という問題なんですが，答えがないんです．先生に聞いても答えが少し違うと言われるだけで・・・．

僕の答えは −ｋｘ＝（Ｉ/Ｒの２乗＋Ｍ）ｘの２階微分なんですが何が間違っているかわかりません．おしえてください．

Re: 無題

Yokkun さんのレス (2008/12/23(Tue) 21:03)

運動方程式はあっているように思いますが．まさか，問題のKとｋの違いとかではないでしょう？

ちゃんと単振動の標準形と比較しろとか，単振動解を出せとか，または，エネルギー保存を単振動一般と同形に書くとか，

ちゃんと証明の形にしなさい，ということでは？

Re: 無題

mNeji さんのレス (2008/12/23(Tue) 21:10)

「x」の定義がハッキリしていませんが，おもりMと滑車がともに静止していて，おもりMとバネが釣り合っている所を座標原点とし，下方に向いておもりMの座標をxとすれば，お書きになった運動方程式で良いと思います．

このような問題の時には，滑車とおもりの間の張力を導入して，・おもりの運動方程式・滑車の角運動量方程式・ひもと滑車が滑らない条件を書いてから，張力や滑車の回転角度などを消去する方が，間違いないと思います．

Re: 無題

なんとなくさんのレス (2008/12/24(Wed) 10:41)

なんとなくです． >Yokkunさん，mNejiさん横から失礼．教えてください．問題文に地面とあるので，運動方程式には，鉛直面内の運動だと重力加速度ｇが出てきそうですが，私が何か勘違いしてるのでしょうか？

Re: 無題

mNeji さんのレス (2008/12/24(Wed) 10:59)

なんとなくさん，

＞鉛直面内の運動だと重力加速度ｇが出てきそうですが

私も最初は錘に対する重力項を考えたのですが，座標原点を，全てが静止してバランスを取っている点と定義すれば，「錘に対する重力項」は「バネの静止バランスでの伸び」に吸収されると思いました．

これから庭仕事の材料購入で出かけますので失礼します．

Re: 無題

なんとなくさんのレス (2008/12/24(Wed) 11:37)

>mNejiさん

お忙しいのに早速お返事有難うございました．平衡点からのずれという意味で，単振動の本質的な部分でないということですね．了解しました．ではもしかすると，先生の指摘は，ちゃんと解ける運動方程式を望まれているのかも知れませんね．問題の意図が奈辺にありや，ということでしょうね．

Re: 無題

Yokkun さんのレス (2008/12/24(Wed) 17:26)

>「錘に対する重力項」は「バネの静止バランスでの伸び」に吸収されると思いました．

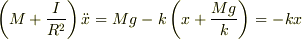つりあいの位置を原点にして，下向きに軸をとると， $\left(M+\frac{I}{R^2}\right)\ddot{x} = Mg-k\left(x+\frac{Mg}{k}\right)=-kx$ ですね．もしくは，ポテンシャルエネルギー 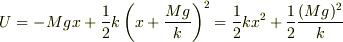$U = -Mgx + \frac{1}{2}k\left(x+\frac{Mg}{k}\right)^2 = \frac{1}{2}kx^2+\frac{1}{2}\frac{(Mg)^2}{k}$ で，第2項が定数でおちます．

[home] [掲示板] [ページの先頭]