電子スピンのベクトル表示

home > 掲示板 >

このページのPDF版

サイトマップ

電子スピンのベクトル表示

ファイルさんの書込 (2008/12/22(Mon) 02:47)

量子力学を復習していたら，わからない部分が出てきたので，よろしくお願いします．

上向きスピンの固有関数を $|\uparrow \rangle=\left[\begin{array}{c}1 \\0\end{array}\right]$ ，下向きスピンの固有関数を $|\downarrow \rangle=\left[\begin{array}{c}0 \\1\end{array}\right]$ とすると任意のスピンの状態ベクトルは

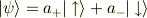
$|\psi\rangle=a_{+}|\uparrow \rangle + a_{-}|\downarrow \rangle$

と表せると理解しています．なので，上の式の 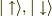$|\uparrow \rangle,|\downarrow\rangle$ は基底ベクトルとして読み取れると思うのですが，ある本を読んでいたところ，「これをスピノルという」と書いてありました．

スピノルというのは良く知らないのですが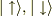， $|\uparrow \rangle,|\downarrow \rangle$ を基底ベクトルと考えることが間違ってるのでしょうか？

Re: 電子スピンのベクトル表示

mNeji さんのレス (2008/12/22(Mon) 10:23)

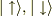＞ $|\uparrow \rangle,|\downarrow \rangle$ を基底ベクトルと考えることが間違ってるのでしょうか？

通常の量子力学の解釈では，電子や核子のような「1/2(half)spin」の粒子の振る舞いをある座標の方向の成分に分けて考えるので良いとおもいます．

しかし，粒子の運動速度が大きく成って来ると，相対論的な量子力学が必要となります．このような拡張に対して「リー群の理論」を展開したフランス人の Élie Cartanさんが系統的に研究したのがスピノールの理論のようです．

ご本人の解説は，数学者の解説とは思えないくらい物理的な説明が明瞭なきがします．図書館ででもご覧に成ってください．ドーバーから安価に出版されるので，個人で購入するのも良いかも知れません．

"THE THEORY OF SPINORS", Dover Pub., Inc., 1966, ISBN: 0-486-64070-1

Re: 電子スピンのベクトル表示

toorisugari no Hiro さんのレス (2008/12/22(Mon) 11:35)

> スピノルというのは良く知らないのですが

このスレッドで簡単に説明するのは無理です．

もし関心があるのでしたらDirac方程式を勉強されることを勧めます．古い本ですが，「相対論的量子力学 (新物理学シリーズ (13))」西島和彦 (著)

http://www.amazon.co.jp/%E7%9B%B8%E5%AF%BE%E8%AB%96%E7%9A%84%E9%87%8F%E5%AD%90%E5%8A%9B%E5%AD%A6-%E6%96%B0%E7%89%A9%E7%90%86%E5%AD%A6%E3%82%B7%E3%83%AA%E3%83%BC%E3%82%BA-13-%E8%A5%BF%E5%B3%B6-%E5%92%8C%E5%BD%A6/dp/4563024139/

が定番です．

概要をつかむだけなら「相対論的物理学のききどころ (物理講義のききどころ (6))」和田純夫 (著)

http://www.amazon.co.jp/%E7%9B%B8%E5%AF%BE%E8%AB%96%E7%9A%84%E7%89%A9%E7%90%86%E5%AD%A6%E3%81%AE%E3%81%8D%E3%81%8D%E3%81%A9%E3%81%93%E3%82%8D-%E7%89%A9%E7%90%86%E8%AC%9B%E7%BE%A9%E3%81%AE%E3%81%8D%E3%81%8D%E3%81%A9%E3%81%93%E3%82%8D-6-%E5%92%8C%E7%94%B0-%E7%B4%94%E5%A4%AB/dp/4000079468/

もあります．

さらに詳しく知りたいならmNejiさんも勧められている本を読まれるといいでしょう．

Re: 電子スピンのベクトル表示

ファイルさんのレス (2008/12/24(Wed) 21:10)

とりあえずは，基底のように考えても問題はないということですね．時間があったら，スピノルを勉強してみます．ありがとうございました．

[home] [掲示板] [ページの先頭]