電子レンジとアルミホイル
電子レンジとアルミホイル
りとるぱんだ さんの書込 (2008/12/19(Fri) 09:53)
はじめまして.学部生2年です.
ふと先日から気になってしまいなかなか納得いく説を考えられません. 電子レンジにアルミホイルをかけると火花が散るのはなぜだと思いますか?
自分ははじめ,光電効果によるものではないかと考えました. 電磁波が自由電子にエネルギーを与えて電子が飛び出し,その電子が電磁波から受けたエネルギーを発散(もしくは空気中の分子とぶつかる?)するから,そのときのエネルギーの発散が火花というかたちで目に見えるのかと思いました.
しかし電子レンジが出す電磁波は振動数が2.45GHzで,その光子がもつエネルギーはアルミホイルの仕事関数(だいたい4eV)にはとうていおよびませんでした.
また,電磁気学の教科書(物理入門コース 4 電磁気学 2)によると電磁波は導体に強く反射される,入射できる厚さはごくわずか,と書かれていました.(実際に波動方程式から具体的な入射できる厚さを導いていました.) ということは導体はものすごく電磁波からエネルギーを受けとりづらいということですか? それとも電磁波の入射できる厚さが薄すぎてほとんど電子しかそのエネルギーを受けとれないということですか? そもそも『強く』反射とはどういうこと?
もし電子だけがエネルギーを受け取るとしたら,電磁波の振動数が低すぎて光電効果を起こさない場合,受けとったエネルギーはどこにいくのでしょう?
電磁波は導体に強く反射されるということは導体と電磁波は互いに影響をおよぼしにくいとう事とは違うんでしょうか? 影響をおよぼしにくいならなぜ電子レンジにアルミホイルをかけるとバチバチなる?
と疑問ばかりわいておてあげです.
量子力学の考え方を理解できてないことが大きいかもしれませんね. 光電効果さえあまり理解できてないみたいです. 後半疑問だらけで読みづらくて申し訳ないです.
よろしくお願いします.
ちなみに一応ぐぐってみたのですが,物理をかじってしかいないようなものばかりで納得いくものはありませんでした….
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/19(Fri) 13:56)
りとるぱんだ さん,始めまして.
私は,中学生のころアマチュア無縁に凝った事があり,真空管で出力10Wの送信機を作り,調整中に送信管の陽極(アノード,プレート)に触って,感電するとともに,指先がすこしえぐれて,硬く焼けた経験があります.ですから,電子レンジの500Wだ,700Wなどの出力を見るに付け,凄い出力だと思います.
さて,電子レンジでの波長を考えると,3GHzの場合,
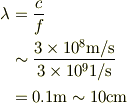
となり,容器のサイズと波長は同程度になりますね.
従って,アルミ・フォイルのようにエッジの立った金属薄膜が,定在波の半波長程度の幅, 〜5cm,であれば,その両端に逆方向の電場を受ける事に成ります.裏返して言えば,大きな静電誘導を起こし得るのではないでしょうか.
その上,電子レンジに数百Wのエネルギが入っているのですから....フォイルのエッジから空気放電するのかも知れませんね.
以上,憶測モードです.
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/19(Fri) 14:02)
> 電磁波は導体に強く反射される,入射できる厚さはごくわずか,と書かれていました. > そもそも『強く』反射とはどういうこと?
電磁波により誘導された表面電流がほとんど逆位相の電磁波を放射して,金属内部での電磁波をほとんどうち消すということです.
Re: 電子レンジとアルミホイル
Yokkun さんのレス (2008/12/19(Fri) 19:32)
アルミホイルでつねに放電が起きるというわけでもないですよね? 特に,ホイルの端どうしが軽く接触したようなところで放電が起きやすい気がします. 実験してみました.5〜10cmほどの長さにさいたホイルをそのまま置いても火花はとびませんでしたが,くるっとループにして端どうしを軽く接触させると強く放電が起きました.5mmぐらいのギャップをつくってもよくとびましたよ.
Re: 電子レンジとアルミホイル
りとるぱんだ さんのレス (2008/12/19(Fri) 19:40)
mNejiさん,返信ありがとうございます.
> エッジの立った金属薄膜が,定在波の半波長程度の幅, 〜5cm,であれば,その両端に逆方向の電場を受ける事に成ります.
金属表面に電場の波(その強さの強弱)があらわれるということですか? だとするとその共振のようなものが起こるのがなぜかよくわかりません….
それは金属表面すれすれを通っていく電磁波の重ね合わせによるものですか?
Re: 電子レンジとアルミホイル
りとるぱんだ さんのレス (2008/12/19(Fri) 19:49)
Yokkunさん返信ありがとうございます.
ごめんなさい,恥ずかしい話,自分で実験してなかったです…. 頭ばかりで考えるより実験とても重要ですね. 実験していただいてありがとうございます.
> 実験してみました.5〜10cmほどの長さにさいたホイルをそのまま置いても火花はとびませんでしたが,くるっとループにして端どうしを軽く接触させると強く放電が起きました.5mmぐらいのギャップをつくってもよくとびましたよ.
なんらかの強力な電場に耐えかねて電子が飛び出すというのは間違いなさそうですね.
ただ上の返信にも書いたように共振のメカニズムがわかりません….
Re: 電子レンジとアルミホイル
りとるぱんだ さんのレス (2008/12/19(Fri) 19:51)
toorisugari no Hiroさん返信ありがとうございます.
> 電磁波により誘導された表面電流がほとんど逆位相の電磁波を放射して,金属内部での電磁波をほとんどうち消すということです.
なるほど,少し自分でも考察してみます.
Re: 電子レンジとアルミホイル
Yokkun さんのレス (2008/12/19(Fri) 20:42)
>ただ上の返信にも書いたように共振のメカニズムがわかりません….
私も詳しくはないのですが… 振動電場によってアルミホイルに高周波電流が生じます.ホイルの端は電流の固定端,電位の自由端になると思います.導体中では高周波は光速に近い速さで伝播するので,mNejiさんがおっしゃったように導体の大きさが半波長に近いと,両端が電流の節=電位の腹になる定常波を生じます.この場合,両端は電位の振幅が大きいため,たとえばループにするとギャップをこえて高い電位差が生じますので,火花放電が起こります.
余談ですが,電球をレンジに入れると光りますが,豆電球を入れても光りません.フィラメントの長さが波長の程度であると,定常波がたってエネルギーを吸収しやすくなるのですが,豆電球では短すぎるのですね.この実験も実はやったことがあるのですが,豆電球に半波長ダイポールアンテナをつけてやると,これが見事に点灯するのです.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/19(Fri) 23:12)
りとるぱんだ さん,
>金属表面に電場の波(その強さの強弱)があらわれるということですか? >だとするとその共振のようなものが起こるのがなぜかよくわかりません….
ご質問の意味が良く判らないので,自分の感触を書かせて頂きます.
電子レンジそのものは,一種の空洞共振器と考えられると思います.恐らく,レンジの内側サイズは,2.5GHzの半波長の整数倍と思われます.ただし,食品などを加熱するのが目的なので,共振は狭い共鳴幅ではなく,幅の広い共鳴幅(言い換えれば,抵抗成分が大きく,効率は低め)と成っている筈です.
ですから,半波長の整数倍の金属が入れば,静電誘導が強く起こると推定した訳です.
ただ,空洞共振器中の電磁波は自由空間の電磁波と振る舞いが違うので,詳しいことは,今の段階では判りかねます.
〜〜〜〜〜〜〜〜〜〜〜〜〜 toorisugari no Hiroさん,
>電磁波により誘導された表面電流がほとんど逆位相の電磁波を放射して,金属内部での電磁波をほとんどうち消すということです.
以前にも,金属中への電磁波の侵入のモデル計算の話題がありました.手元に,その手の分野の教科書がないので間違いかも知れませんが,金属に侵入した電場成分は,それに比例した電流を生じるので,ジュール熱に基ずく減衰型の波動方程式に従うので,結果として侵入成分が大きく成らず,入射電場の大部分が反射電場に戻るのではないでしょうか.
〜〜〜〜〜〜〜〜〜〜〜〜〜〜 Yokkunさん,
>実験してみました.5〜10cmほどの長さにさいたホイルをそのまま置いても火花はとびませんでしたが,くるっとループにして端どうしを軽く接触させると強く放電が起きました.5mmぐらいのギャップをつくってもよくとびましたよ.
興味深い結果ですね.なんとなく,静電誘導と言うよりは,電磁誘導みたいな現象に近いのかも知れませんね.ループの方向を替えると,放電の頻度が変わるとか?
>豆電球に半波長ダイポールアンテナをつけてやると,これが見事に点灯するのです.
これは愉快ですね.高校の理科の実験に使うと教育的ですね.上のループ現象も含め,空洞共振のモードを調べてみないといけなさそうですが,時間が掛かりそうです.
また,もし壊れた小型蛍光灯(点灯回路などの付いていない)をいれるとアンテナなしに点灯すると思います.
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/20(Sat) 00:19)
> 金属に侵入した電場成分は,それに比例した電流を生じるので,ジュール熱に基ずく減衰型の波動方程式に従うので,結果として侵入成分が大きく成らず,入射電場の大部分が反射電場に戻るのではないでしょうか.
意味がよくつかめませんが,反射する原因は抵抗によるジュール熱によるということでしょうか?それなら,完全導体では反射は起きないということになりますね.
おっしゃっるのは,
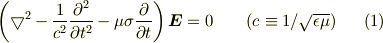
の事でしょうが,  は電気伝導度であって,抵抗に反比例します.
ですから,ジュール熱で減衰しているわけではないのです.
は電気伝導度であって,抵抗に反比例します.
ですから,ジュール熱で減衰しているわけではないのです.
これは侵入電場の厚さを記述する式だと考えるべきでしょう.
電磁波の角速度を  とします.(1)式は
とします.(1)式は
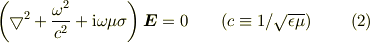
となります.電気伝導度が十分に大きい( 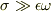 )と,(2)式の
)と,(2)式の 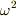 の項((1)での時間の2階微分項)が落ち
の項((1)での時間の2階微分項)が落ち
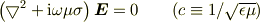
となります.
これにより,電場が侵入する厚さ(=表面電流が流れる厚さ)は 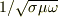 程度と非常に薄いことが導出されます.電気伝導度が大きくなるとより薄くなります.表面の薄い領域より奥では電場は完全にうち消されてしまいます.
程度と非常に薄いことが導出されます.電気伝導度が大きくなるとより薄くなります.表面の薄い領域より奥では電場は完全にうち消されてしまいます.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/20(Sat) 08:28)
>反射する原因は抵抗によるジュール熱によるということでしょうか?それなら,完全導体では反射は起きないということになりますね.
ジュール熱という表現を用いたのは,エネルギ散逸という非可逆的過程を意味すると思い,用いました.まさに「侵入電場の厚さ」が出て来るのは,エネルギ散逸がある事が重要ではないですか?
また反射を支配するのは,金属表面における電場; ・入射波 ・侵入波 ・反射波 の3成分で境界条件が決まることが本質的だろうと思います.侵入波が成長しないいじょう,反射波が大きくなると考えても良いと思いますが....
>表面の薄い領域より奥では電場は完全にうち消されてしまいます.
なにか直感的には捉えにくい描像ですね.静電気的な説明と波動的な説明とがぶつかっている様に感じます.
>完全導体では反射は起きない
以前にも,この論議をされていたように思いますが,私には理解出来ませんでした.ただし,本スレッドのような日常現象の論議に,特殊な場合を細かく論議するのは適切ではないでしょう.他のスレッドを立ち上げる方が良いのかも知れません.
#これから外出するので,夜までご返信できません,悪しからず.
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/20(Sat) 10:22)
> エネルギ散逸がある事が重要ではないですか?
反射にエネルギー散逸は邪魔でありこそすれ,不要です.
先の式で考えると抵抗が大きくなるほど,侵入距離は大きくなります.
これは電子が抵抗のため動きづらくなり,電磁波に十分に追従できないため,誘導電磁波で十分にうち消すことができなくなるからです.
侵入波が散逸により消えるのなら,それはエネルギーが吸収され熱などに変わることであって,(コヒーレントな)反射波は発生しません.発生したら熱力学第2法則に反します.(黒体放射は出るかもしれませんが.)
- 波のエネルギーを保ちながら侵入波を消すには干渉しかあり得ません.このとき,エネルギー保存則により反射波が発生します.
> 侵入波が成長しないいじょう,反射波が大きくなると考えても良いと思いますが....
同じ論理を散逸が支配的な物体である「黒体」につかうと,「黒体」が金属光沢を持つことになってしまいます.
> 静電気的な説明と波動的な説明とがぶつかっている様に感じます.
私は「静電気的な説明」は一切していません.それをされているのはmNejiさんです.
Re: 電子レンジとアルミホイル
なんとなく さんのレス (2008/12/20(Sat) 12:51)
横レス失礼します. 少し議論がずれているようですが,レス主の最初の疑問に戻ってみると,Yokkunさんの実験に端緒なように,この状況は電(磁)波とアンテナの関係,つまり電磁誘導の観点から考えるのが妥当だと思います.かのヘルツの実験の再現ですね. 混乱は導体のサイズと電磁波の振動数の兼ね合いです.電磁波の導体進入などを論議する場合は導体(のサイズ)に比べて,波長が小さい場合です.なぜなら波の回り込み(回折)を考慮しない場合だからです.逆にサイズが同じくらい(オーダー)であると,丁度LCR回路のように交流に対する共鳴(共振)が起こると考えられます.導体内部に電磁波はなくとも,電流は流れます.もちろん回路に成らねばなりませんので,ギャップを通して回路が形成されます.最大共振条件としては波長の(半)整数倍などですが,もちろん厳密でなくとも起こりえます. まとめると,電子レンジの固有周波数が同サイズの導体アルミホイルをアンテナとして,電波の吸収・反射を繰り返しているが,ギャップがあるとそこに電流回路が生じ,電波のエネルギーを吸収して火花を飛ばす,ということでは無いでしょうか.ちなみに取説にもあるでしょうが,この実験は危険を伴います.なぜなら,”空焚き”と近いからです.レンジ本体を痛める可能性がありますので,注意が必要と思われます.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/20(Sat) 20:09)
toorisugari no Hiroさん,
金属に対する電場の侵入についてのご論議は,私には理解できません.電磁波であろうと,回路であろうと,抵抗成分は本質的にジュール発熱するものだと思います.
例えば,抵抗Rに電圧Vが加われば,V=RIに従って電流Iがながれ,その時の発熱量Wは, W=IV=(V^2)/R ですので,抵抗が小さい程,発熱が大きいのだと思います.
ただし,自分が読んだ資料は手元に無いので,上記の現象についての論議は保留させてください.自分の理解の正否も含めて勉強し直したいと思いますが,時間が掛かりそうですので,悪しからず.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/21(Sun) 19:35)
りとるぱんだ さん,
「電子レンジ原理」で検索して見ましたがあまり良く判りませんでした.ただし,電子レンジは,空洞共振というよりは,発信器から出てきた電磁波は進行してきて,散乱を繰り返すような構造らしいですね.ついては,「空洞共振」的な説明は取り下げます,ご免なさい.
どうやら,天井側から加熱が進行する見たいでした.これもまだ明確ではありませんが....
検索中に面白そうだったサイトを独断と偏見で選んでみました(笑).
(1)電子レンジに蛍光灯を入れてみよう ←実験する時の参考(空焚き防止)にもなるようです. ttp://www.gijyutu.com/kyouzai/denki/hoden.html
(2)第3回電子レンジで火の玉 ←迫力ある火の玉ができるらしい. ttp://homepage3.nifty.com/s-danjo/electro/hitama/hitama.htm
(3)【ニューセラミック手造り豆腐茶碗】 ←容器がジュール加熱の積極的な利用. ttp://www.fkco.jp/tofustation/tsukurikata_tofubowl.html
なお,空洞共振については,うろ覚えです.いろいろ検索しているうちに,次のサイトを拝見しました;
(4)導波管と空洞共振器 ttp://w3p.phys.chs.nihon-u.ac.jp/~takizawa/tex/micro1/node2.html
(4a)導波管のなかの電磁波 ttp://w3p.phys.chs.nihon-u.ac.jp/~takizawa/tex/micro1/node4.html
(4b)二つの平行な平面鏡間の波 ttp://w3p.phys.chs.nihon-u.ac.jp/~takizawa/tex/micro1/node3.html
要は,境界が金属である場合,自由空間での電磁波と振る舞いが異なって,縦波のモードが存在することです.「(2)の実験」や「Yokkunさんの実験: No.22524」を拝見していると,TM波モードが主要なのかも知れません.
この分野にお詳しい方がいらしたら,是非とも解説をお願い戴ければ幸いです.
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/22(Mon) 11:20)
> 抵抗成分は本質的にジュール発熱するものだと思います.
別にそれに異をとなえてません.反射は散逸(=ジュール発熱)に因るものでないというだけです.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/22(Mon) 12:20)
>反射は散逸(=ジュール発熱)に因るものでないというだけです.
私もそう思います.反射を直接的に支配するのは表面での境界条件です.
しかし,内部への進行波がジュール発熱による減衰を起こさなければ透過量が増大してしまうでしょう.その意味では,間接的に内部での減衰が,反射量の増大に寄与していると思います.
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/22(Mon) 12:58)
論点の違いがはっきりしましたね.
> 内部での減衰が,反射量の増大に寄与していると思います.
内部での(散逸による)減衰が,反射量の減衰に寄与していると思います.
# 追記しました.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/22(Mon) 20:17)
本スレッドのご質問と少し問題がかけ離れているとは思いますが,金属からの反射について,さらにコメントをさせて頂きます.
なお,話の流れから,自由空間を進んできた横波の平面波が金属に垂直に入射することを論じます.ただこの場合,どのようにモデル化をしたか,今だ明確におもいだせないので,定性的なコメントにとどめます.
>> 内部での減衰が,反射量の増大に寄与していると思います.
始めに理科年表で「金属の分光反射率(600nm) 単位%」と「金属の体積抵抗率(0℃)単位:nΩm」について調べると <pre> % nΩm Al 91.1 25.0 Ag 98.1 14.7 Au 91.9 20.5 Cu 93.3 15.5 Rh 79.9 43 </pre> となり, 「反射率は高い」<=>「抵抗が低い」 事が判ります.
問題は,「抵抗が低い」というのは,どのような現象と対比させるべきかでしょう.
当然の事ですが,真空を進行する平面波は,いくら進んでも,その電場なり磁場の強度は減衰しません.しかし,その電場が金属に侵入始めると,金属の伝導電子を駆動するにつれて電場強度は減衰する訳です.
電流が駆動される時に発生するエネルギ損失は,定電圧回路系でも良く知られているように,W = IV = (V^2)/Rと,抵抗値が低い程,大きなジュール熱を生じるわけです.定電圧回路系の一例として,電池を考えると,化学的エネルギでジュール熱を補う訳ですね.金属中に進行する電場では,後方からの来る電場が持ち込むエネルギしか供給もとがないので,抵抗が小さい程,急速に電場強度が減少して,侵入が切られると考えていい訳だと思います.
逆に言えば,抵抗R→0の極限では,微小でも侵入した途端,侵入電場がエネルギ減少をしてしまうので侵入できないと解釈すればいいでしょう.
もちろん,金属中の電磁波のモデルを立てて,その波動方程式を吟味すれば,上記の定性的な挙動は説明可能とおもいます.残念なことに,参考資料を見ないと,その論議はできません.
逆に >内部での(散逸による)減衰が,反射量の減衰に寄与していると思います.
というのは,どのような関係から結論されるのでしょうか?
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/22(Mon) 21:02)
> 電流が駆動される時に発生するエネルギ損失は,定電圧回路系でも良く知られているように,W = IV = (V^2)/Rと,抵抗値が低い程,大きなジュール熱を生じるわけです.
電子は加速度運動をしているので,電磁波を放出するはずですが,どうしてここで,抵抗によるエネルギ損失「しか」考えないのでしょうか?
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/22(Mon) 21:51)
>電子は加速度運動をしているので,電磁波を放出するはずですが,どうしてここで,抵抗によるエネルギ損失「しか」考えないのでしょうか?
どこまでをモデルに取り込むかどうかの部分の話と,定性的な論議により大筋の傾向を掴むかの問題でしょう.私の説明は,前にも申し上げた様に,以前勉強した本を見直してからにします.
むしろ,ご自分の筋書きを解り易く説明して頂けませんか. >内部での(散逸による)減衰が,反射量の減衰に寄与していると思います.
の関連が明白とは思えないからです.
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/22(Mon) 23:00)
> むしろ,ご自分の筋書きを解り易く説明して頂けませんか.
何を持って解り易くか分かりませんが,ご希望ならオームの法則とMaxwell方程式から(1−反射率)が伝導率と透磁率の積の平方根に反比例する事を導出しましょうか?
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/23(Tue) 00:11)
>オームの法則とMaxwell方程式から(1−反射率)が伝導率と透磁率の積の平方根に反比例する事を導出しましょうか?
面白そうですね.宜しくお願いします.
なお,No.22533 でお書きになった, >波のエネルギーを保ちながら侵入波を消すには干渉しかあり得ません.このとき,エネルギー保存則により反射波が発生します.
の点について,是非とも解釈くだされる事を希望いたします.
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/23(Tue) 01:28)
長いです.
直線偏光した角速度  の電磁波が金属に垂直に照射するときの反射と透過について考える.金属面の法線方向を
の電磁波が金属に垂直に照射するときの反射と透過について考える.金属面の法線方向を  とし,
とし, 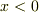 で真空,
で真空, 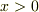 で金属とする.
で金属とする.
仮定1. オーム法則が成り立つ:金属内に電磁波がかかるとき,その周波数はプラズマ周波数より十分低いとして, 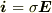 の電流密度が発生するとする.ただし,
の電流密度が発生するとする.ただし,  は電気伝導率.なお,電気的に中性なので電荷密度は0のままである.
は電気伝導率.なお,電気的に中性なので電荷密度は0のままである.
仮定2. 電気伝導率は十分に大きい:金属での誘電率を  ,電磁波の角速度を
,電磁波の角速度を  とすると
とすると 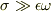 (金属と,高周波電波では成り立つ.)
(金属と,高周波電波では成り立つ.)
仮定1およびMaxwellの方程式より,
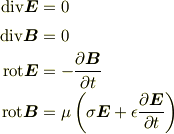
と与えられる(ただし, 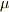 は金属の透磁率).これらと
は金属の透磁率).これらと 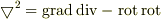 より
より
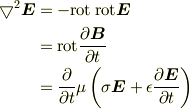
となるから,金属中の電磁場の基礎方程式
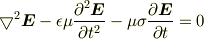
が得られる.( 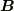 についても同様の式なので省略する.)
についても同様の式なので省略する.)
ここで,電場の式
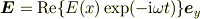
を代入すると,
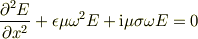
さらに仮定2より
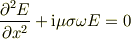
が得られる.
また,真空中では
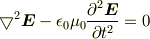
より,
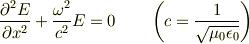
であるから,
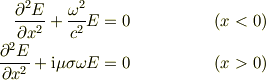
が場の強度を支配する方程式である.
この解として
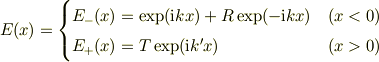
を仮定する.ただし, 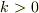 である.
である.
上式に代入し接続条件 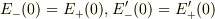 を用いると,
を用いると,
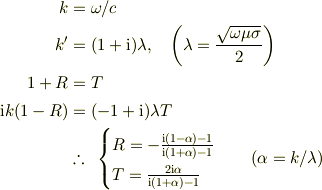
が得られる.ただし, 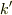 の符号として
の符号として 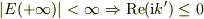 となるものを選んだ.また,仮定2と金属では
となるものを選んだ.また,仮定2と金属では 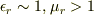 より
より
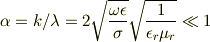
であることを考慮すると,
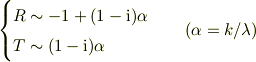
である.
反射率は 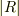 に相当するが,
に相当するが,
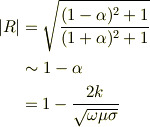
となり,これより抵抗が大きいと反射率は減少することが分かる.
また, 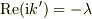 より
より 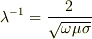 が電磁波の侵入距離であり,抵抗が大きいと侵入距離は長くなることも分かる.
が電磁波の侵入距離であり,抵抗が大きいと侵入距離は長くなることも分かる.
# [追記12/24]  の式を間違えていたのを訂正しました.
の式を間違えていたのを訂正しました.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/23(Tue) 03:27)
>長いです.
お疲れ様です.
自分で書き下すのをサボっていたので,
> 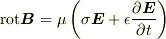 が出て来ませんでした.お恥ずかしい.
が出て来ませんでした.お恥ずかしい.
さらに
>さらに仮定2より
> 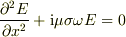
なるほど,良く判りました,有り難うございます.
細かい話ですが,この特解を 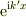 と仮定すると,
と仮定すると, 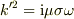 ですから,固有値は
ですから,固有値は
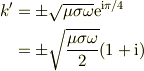
となり,遠方解が発散しない為に負の符号だけが残るのですね.
しばらく検討してから,明日にでもコメントいたします.
なお,通常の回路でのジュール発熱, 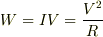 に対応する量は,発熱密度;
に対応する量は,発熱密度;
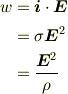
だとおもいます.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/24(Wed) 10:51)
自己コメントです.
>しばらく検討してから,明日にでもコメントいたします.
と思っていたのですが,先週末の強風で庭の木に損傷が強く,今日も素人庭師を続行することになりました.コメントは遅れます.
以前,量子力学の矩形ポテンシャルのご質問で,確率密度や確率流の論議がありましたが,今回の問題は古典的電磁気の問題ですから,ある単位面積に着目して,表面(x=0)での入射波と反射波のエネルギ流(Poynting vector)と金属内の全ジュール発熱(x=0〜+∞)とで,エネルギ保存を考えれば良いのではないかと推定しています.
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/24(Wed) 11:49)
> 細かい話ですが,この特解を 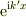 と仮定すると,
と仮定すると, 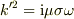 ですから,固有値は
>
ですから,固有値は
>
> となり,遠方解が発散しない為に負の符号だけが残るのですね.
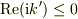 が
が 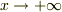 で発散しない条件なので,正の符号が残ります.
で発散しない条件なので,正の符号が残ります.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/24(Wed) 23:55)
> 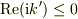 が
が 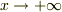 で発散しない条件なので,正の符号が残ります.
で発散しない条件なので,正の符号が残ります.
おっと,間違えていますね.「座標の負方向」の場合,確認した積もりが,二重に間違って,正解に見える時がしばしばあります(泣).余程,算数や数学の神に見放されているのでしょう.
今しばらく,検討してみます.
Re: 電子レンジとアルミホイル
komagatake さんのレス (2008/12/26(Fri) 15:06)
難しい話が続いています. 私には理解できないことです.
元々の質問,アルミホイルの端から起こる火花の発生の説明になっているのでしょうか.
乾電池に豆電球をつないで回路を作った時,導線を電池の腹に擦り付けると火花が飛びます.多分導線が接触したり,離れたりするからでしょう.スイッチの断続で火花が飛ぶのは誘導電流で説明されています.それと同じ理由になるだろうと思います. 「放電」と言いますが電子がただ移動するのであれば目には見えません.目に見えるということは空気がイオン化されている事になります.空気中での放電が起こるために必要な電圧は1cmにつき1万V程度だそうです.これは電場勾配で考えたものですから0.1mmで100V程度です 乾電池で火花放電が見えるということですから元の電圧が1V程度であっても誘導された電圧はずっと高いものになっているという事になります.100倍程度は高くなっているはずです.(高電圧発生装置の誘導コイルはバッテリーで動かすことが出来ます.誘導回路を用いることで100倍から1000倍の電圧を発生させています.詳しいことは分かりませんが多分スイッチの断続に相当する回路を組み込んでいるのでしょう.)
電子レンジのような高周波がかかっている場合にも誘導電圧で放電が起こったときと同じようにアルミホイルのギャップの間に高い電圧が生じるとすると説明ができる事になります.
・電子レンジの中に入れた電球が光るというのとは仕組みが異なります.電球が光るというのは抵抗による発熱(ジュール熱)です.
・具体的にどれくらいの電圧が発生可能かということについては私には分かりません.
空気がイオン化されるということは化学反応が起こっているということです.電子の移動に伴って起こる反応は酸化・還元反応と呼ばれています. 溶液の中に電極を入れた時に起こる電気分解も酸化・還元反応です. 電気分解に必要な電圧は数Vです.でもこの数Vの電圧は2つの極板の間で一様な電場勾配を作っているのではありません.かけた電圧のほとんどは極板から数μmの領域に勾配を作っているということです(分解電圧は電解槽の大きさにほとんど関係しないというのはこのことから出てくることです).1μmで1Vであれば1cmで1万Vです.空気中の放電でも溶液中での電気分解でも必要な電場勾配は同じ程度だということが分かります.同じ性質の化学反応が起こっているということになりそうです. どちらの反応も電極表面に接触している(衝突してきた)物質の上で起こるものです.電極との距離はnmのレベルです.2つの電極の間に置かれた孤立した原子や分子の上で起こる変化ではありません.イオン化エネルギーの数値がそのまま当てはまるものではないだろうと考えています.・
光電効果を考えるというのとは方向が違いますが参考になりますでしょうか. (間違っているかもしれません.私も知りたいことなのであえてこういう文章を書きました.間違っていたら訂正してください.)
※火花放電で光が見えるのはイオンによるものだと書きました.抵抗での発熱(ジュール熱)で光っているのではないということです.アルミニウムの破片が加熱されて飛び散っているのではないはずです.空気の分子の温度が電子の衝突でエネルギーを貰って高くなり発光しているというのもありえません.電子の衝突で分子の運動エネルギーがそれほど大きく変わるとは思えません.質量に10万倍近い違いがあるのですから. (真空管(真空放電管)の中での放電は目には見えません.放電電極にアルミを使ったからといってアルミニウムの破片が熱で飛び散るなんてことは起こりません.)
※金属の光電効果での仕事関数というのは原子のレベルで言うとイオン化エネルギーに相当するもののはずです.水素原子のイオン化エネルギーは13.6eVボルトです.水素の関係する化学反応はありふれたものです.そういう化学反応を考える時に13.6eVという数字を持ってきても何の判断の助けにもなりません.大きすぎます.水素の関係する反応には遊離のH+が出来るイオン化反応は絡んでいないということになります.化学反応の可能性のある場面に化学反応の場以外で求められた物理的な数値をそのまま持ち込むことは出来ないのです.
※1eVのエネルギーは波長で言うとほぼ1μmです.10eVで0.1μmです.可視から紫外の範囲だということになります.マイクロ波は赤外領域よりもまだ長い波長の領域に対応していますから光電効果に原因を求めるのは無理だということになります.
※おまけ(完全な蛇足) ガスバーナーで空気の量とガスの量をうまく調節するとかなりの高温がでます.勢いよく燃えている時の炎の色は青いです.ここで炎の色が青いからと言って「黒体輻射の理論」を持ち出してくると変な事になります.オレンジ色に見える太陽の表面温度が約6000℃ですから青い光の見える炎の温度はもっと高いはずだと判断してしまうことになります.でも都市ガスではせいぜい2000℃前後です.見えているのは反応の途中で出来るメタンの破片(ラジカル)の発光です.ブタンでもプロパンでも同じような青い色の炎が見えます.電線の被覆の塩化ビニールを燃やすと紫色の炎が出ます.かなり低い温度での燃焼ですが紫色が見えます. (教育実習できた物理学科の学生がよくこういう間違いをします.)
Re: 電子レンジとアルミホイル
toorisugari no Hiro さんのレス (2008/12/26(Fri) 15:21)
> 元々の質問,アルミホイルの端から起こる火花の発生の説明になっているのでしょうか.
スレ主さんの >> 電磁波は導体に強く反射される,入射できる厚さはごくわずか,と書かれていました. >> そもそも『強く』反射とはどういうこと?
という質問にこたえているつもりですが.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/27(Sat) 08:58)
komagatakeさん,興味深いご説明とおもいます.
>空気がイオン化されるということは化学反応が起こっているということです.電子の移動に伴って起こる反応は酸化・還元反応と呼ばれています. >溶液の中に電極を入れた時に起こる電気分解も酸化・還元反応です. >電気分解に必要な電圧は数Vです.でもこの数Vの電圧は2つの極板の間で一様な電場勾配を作っているのではありません.かけた電圧のほとんどは極板から数 μmの領域に勾配を作っているということです(分解電圧は電解槽の大きさにほとんど関係しないというのはこのことから出てくることです).1μmで1Vであれば1cmで1万Vです.空気中の放電でも溶液中での電気分解でも必要な電場勾配は同じ程度だということが分かります.同じ性質の化学反応が起こっているということになりそうです.
溶液系の話まで出て来て,なるほどとおもいました.ただ,水溶液に限定すれば,誘電率が高い分,電場の振る舞いは,よりアクティブになるように感じましたが,如何でしょうか?
Re: 電子レンジとアルミホイル
komagatake さんのレス (2008/12/27(Sat) 16:48)
>ただ,水溶液に限定すれば,誘電率が高い分,電場の振る舞いは,よりアクティブになるように感じましたが,如何でしょうか?
電極表面の近くに存在する境界層の厚みがμmの程度だと書きました. この厚みは溶液の中の電解質濃度によって影響を受けるそうです. 厚みが変われば電場勾配が変化します.
誘電率はある意味でマクロな量です.考えている電荷の周りにある電荷を環境として均してしまった場合に出てくる量でしょう.水の誘電率という場合は水の持つ極性の影響を均して見たマクロな量です.
もし電極から離れた所にあるイオンが電極に引っ張られて極板上に来るということであれば全体としての誘電率が大きく影響します.でも電極の影響がイオンに及ぶ範囲は境界層の中だけです.電極間の距離が1cmあっても数μmの厚みを除いた部分では電場の勾配は存在していないのです.引力は働いていないということです.イオンの移動は濃度勾配による拡散だけで起こります.濃度勾配は電気分解が起こる事によって生じますから電気分解が起こらない限りイオンの拡散移動もないということです.(よく図に書かれている正のイオンが陰極に向かって移動し,負のイオンが陽極に向かって移動して行って極板上で反応するというイメージは成立しないものです.) 境界層を作るのは電解質の働きです.境界層の外側にあるイオンに電場が働かなくなるというのも電解質の働きです.スクリーンされてしまうという電磁気の練習問題で扱われている内容のことが起こっているのだと思います.水だけしかなければ電気分解の実現は難しくなってきます.電場勾配が一様になりますから1cmで1V程度であれば電場勾配が小さすぎるのです.水だけの場合でも1cmにつき1万V程度の電圧をかければ流れる事になるだろうと思います.絶縁破壊といわれているものはこの現象でしょう.(ここまで来ると空気中の放電での絶縁破壊も似たイメージで考えていいのではないかと思えてきます.)
イオンでなければ反応しないというのでもありません.水溶液の場合で言うと 2H2O+2e^-→H2+2OH^- は起こります.溶液の中のH+(正確にいうとH3O^+)の濃度が高ければH^+が反応しますがそうでなければH2Oが反応します.高等学校の教科書でも中性付近およびアルカリ性の溶液の中での反応はこの式が書かれています.10年ほど前に書きかえられました. それまでは水素の発生はいつも 2H^++2e^−→H2 でした. H^+の濃度が小さい時も水の分子H2Oの解離で供給されるH+が反応するとしていました.でも解離平衡の移動によるH^+の発生は泡がぶくぶく出るような反応を説明するような速さでは起こらないということで否定されてしまったのです.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/27(Sat) 18:24)
>電極表面の近くに存在する境界層の厚みがμmの程度だと書きました. >この厚みは溶液の中の電解質濃度によって影響を受けるそうです.
水分子のサイズはオングストローム程度ですね.境界層の厚みがμm程度としても,数千,少なくとも数百程度はある訳です.水分子の平均場的な特徴は境界層の電極近辺でもあるような気がしますが....水溶液系と有機溶媒系で,反応速度などで,違いは無いのでしょうか?
Re: 電子レンジとアルミホイル
komagatake さんのレス (2008/12/27(Sat) 21:56)
>水分子の平均場的な特徴は境界層の電極近辺でもあるような気がしますが
サイズから言うと確かにそうですね.
でも反応自体はμmの距離をジャンプして起こるのではなくて極板の上に張り付いた形で起こるようです.電子の移動は極板上で起こるということです.オングストロームレベルだということになります.
極板の作る電解の影響を受けてイオンの分布が変わるというようなことが起こる範囲がμmということのようです.
電気化学の理論は難しくて分からないことが多いです.本によって理論のレベルに差があるという面もありそうです. でも空気中の放電でも,水溶液の電気伝導(これは電気分解の結果です.)でも,摩擦電気でも化学的な考察をしないといけないのではないかと思っています.
元に戻ります. 私としては電子レンジの高周波が放電に必要な電圧を生じさせることが出来るのか否かというところが知りたいです. 交流電圧をかけると誘導コイルで高電圧を発生させたのと同じようなことが起こるとしていいのでしょうか.私にはそういう面での知識がありませんので知りたいと思っているところです,. 折り曲げたアルミホイルのギャップの大きさが火花が見えるかどうかに関係しているようですのでやはり火花放電が起こっているのだろうと考えています.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/28(Sun) 00:56)
>でも反応自体はμmの距離をジャンプして起こるのではなくて極板の上に張り付いた形で起こるようです.電子の移動は極板上で起こるということです.オングストロームレベルだということになります.
なるほど,「電子のジャンプ」といった素過程では,廻りの環境に依存しなくなるのですかね.難しすぎて判りません.
>私としては電子レンジの高周波が放電に必要な電圧を生じさせることが出来るのか否かというところが知りたいです.
とても粗い話で恐縮ですが,電子レンジの発信器からレンジに向かって,自由波みたいなポインティング・ヴェクタSを考えると,入射面積Aとし,自由波の電場強度 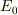 ,平均電磁エネルギ密度
,平均電磁エネルギ密度 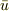 ,レンジの定格出力P
,レンジの定格出力P
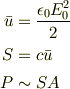
とすると,
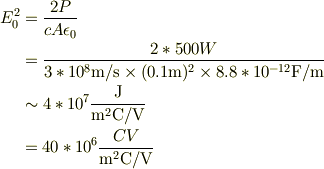
だから
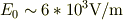
ぐらいとなります.少ないのは,共振を考えていないからか?
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/28(Sun) 01:15)
中断して時間がたってしまいました.金属内部での発熱量を考えて見ます.toorisugari no HiroさんのNo.22565を元に計算します.
電場を成分表示し,
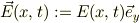
とします.
以後,解り易くする為に,真空側の入射波の成分強度 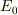 (実数)を明示的に書くと
(実数)を明示的に書くと
![E(x,t) = \begin{cases}\mathrm{Re}[E_0\mathrm{e}^{\mathrm{i}(kx-\omega t)} + RE_0 \mathrm{e}^{\mathrm{i}(-kx-\omega t)} ]& (x<0)\\ \mathrm{Re}[TE_0 \mathrm{e}^{\mathrm{i}k'x -\omega t)}] & (x>0) \end{cases}](http://hooktail.maxwell.jp/bbslog/388f5819dc1efb23da9ad87993d46221.png) を仮定する.
を仮定する.
金属中の発熱量 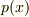 は,ジュール発熱の時間平均で与えられるから,
は,ジュール発熱の時間平均で与えられるから,
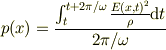
ここで,
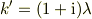
であり,透過係数は絶対値と位相角で表すと
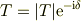
だから,
![E(x,t)&=\mathrm{Re}[E_0T\mathrm{e}^{\mathrm{i}(k'x -\omega t)}]\\&= E_0|T|\mathrm{e}^{-\lambda x}\mathrm{Re}[\mathrm{e}^{\mathrm{i}(\lambda x -\omega t) -\delta}]](http://hooktail.maxwell.jp/bbslog/6f5b7b6762db41890a31614bac89325f.png)
指数部分の自乗の時間平均は1/2に等しいから,
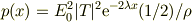
金属中の積分より
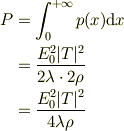
ここで,No.22565の計算から,
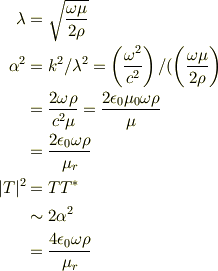
だから,
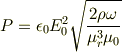
となる.金属内部のジュール発熱は,体積抵抗率の平方根に比例して増大する.もともとのジュール発熱密度が体積抵抗率に逆比例しているのと逆の振る舞いを示しています.
この現象は,抵抗率が大きい程,ジュール発熱密度が低く,その結果,金属中の電場が深く侵入し,全体的なジュール発熱が大きく成ると思われます.言い換えれば,完全導体のような金属では,少しでも侵入すると大きな発熱を伴う為に,金属中に電場が侵入できないと考えられると思います.
これは,壁にたいする反発係数  のボールの反射に似ていて,
・e=1 完全弾性衝突だとエネルギ損失無し<--> ρ=0, 完全導体
・e〜0 非弾性衝突で,ほぼ熱エネルギ<--> ρ=大,不良導体
のボールの反射に似ていて,
・e=1 完全弾性衝突だとエネルギ損失無し<--> ρ=0, 完全導体
・e〜0 非弾性衝突で,ほぼ熱エネルギ<--> ρ=大,不良導体
なお,完全導体で「エネルギ損失無し」というのは,今回のモデルでは,金属電子の運動方程式を無視した為に,緩和時間的な要素が入らなかった為と推察されます.
Re: 電子レンジとアルミホイル
mNeji さんのレス (2008/12/30(Tue) 23:35)
自由区間での入射波(in-coming)と反射波(out-going)とのエネルギ密度の流量(時間平均)を求めると;
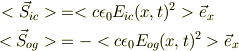
ここで,
![E(x,t) &= E_{ic}(x,t) + E_{og}(x,t)\\E_{ic}(x,t) &= \mathrm{Re}[E_0\mathrm{e}^{\mathrm{i}(kx-\omega t)}]\\E_{og}(x,t) &= \mathrm{Re}[RE_0\mathrm{e}^{\mathrm{i}(-kx-\omega t)}]](http://hooktail.maxwell.jp/bbslog/51c2bd089f0adbd02ca3b78091180fe7.png)
x軸に沿って,金属に流入するエネルギ密度の時間平均は;
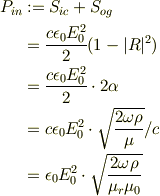
金属内部のジュール発熱;
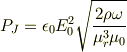
と比較して
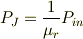
となる.
今の所,不一致の理由は判りません.残念な事に,来年に問題持ち込みとなってしまいました.;-P
この計算中に,「金属光沢電磁気」で検索したところ,下記の資料を拝見しました;
・金色の物理的起源(PDF) home.sato-gallery.com/education/kouza/metal_color_seminar.pdf
なんとなく,昔読んだ本の解説に似ている様な気もします.当時は,この手の説明を見て納得できなかったのを思い出しました.