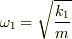二重バネ連合
二重バネ連合
けんじ さんの書込 (2008/12/17(Wed) 16:07)
はじめまして 課題がわからないのでよろしくお願いします
質量m1,m2,ばね1(バネ定数k,自然長l1),ばね2(バネ定数k,自然長l2)があり
(壁)|ー(ばね1)−(質量1)−(ばね2)−(質量2) ___|________________________
といったようになっている. 質量m1,m2の平衡点x1=l1x2=l1+l2 からの変位をそれぞれy1,y2とする
「A」m1=m2のとき (1)ポテンシャルUは2*2行列を使って
- U=1/2(y1,y2)K(y1)
- y2
↑1*2行列↑2*1行列
とあらわすことができる Kを求めろ
(2)直行行列Rをもちいて,座標y1,y2を (y1)=R(q1) y2q2
のように一次変換すると U=1/2(q1,q2)R^T KR(q1) q2
といったように,Uはq1,q2の二次式として表せれる
このとき直行行列Rをうまく選べば
行列R^TKRが対角形=(k10) 0k2←2*2行列
になることが知られている.このようなk1,k2を求めろ
(3)ラグランジアンを新しい変数q1,q2を用いて表し,q1(t),q2(t)に対する運動方程式を書き下し,そのかいq1(t),q2(t),を求めろ.それから2質点の運動y1(t),y2(t)を書き下せ
「B」m1=m2とは限らない一般の場合 z1=(√m1)y1 z2=(√m2)y2
と一次変換したとき,二質点の運動y1(t),y2(t)はどのようになるか
醜いですが本当に困っています よろしくお願いします
Re: 二重バネ連合
Yokkun さんのレス (2008/12/17(Wed) 19:34)
問題のレベルからいって,とても「教える」立場には立てそうにないですが,アドバイスしながら一緒に解くことはできそうです.
で,まず(1)ですが,ポテンシャルエネルギーを 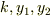 を使って書けばどうなりますか?そして,
を使って書けばどうなりますか?そして,
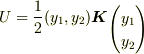 となる
となる
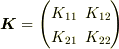 を求めましょう.
を求めましょう.
Re: 二重バネ連合
けんじ さんのレス (2008/12/17(Wed) 19:48)
アドバイスよろしくお願いします
題意より U=1/2ky1^2+1/2k(y2−y1)^2
=1/2k{2(y1)^2−2(y1)(y2)+(y2)^2}
また U=1/2{K11(y1)^2+(K12+K21)(y1)(y2) +K22(y2)^2}
二式より K11=2k K12+K21=−2k K22=k
自分でやってみたのですがどうですかねぇ・・・
Re: 二重バネ連合
Yokkun さんのレス (2008/12/17(Wed) 20:11)
いいと思います. 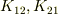 のとり方はいろいろありますが,一般の場合にどうなるかは私もまだよく検討していません.
そこでおすすめですが,対称な
のとり方はいろいろありますが,一般の場合にどうなるかは私もまだよく検討していません.
そこでおすすめですが,対称な 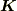 を選びませんか?
その上で,(2)にすすみましょう.(2)は
を選びませんか?
その上で,(2)にすすみましょう.(2)は  において2つの座標の積の項がなくなるように,座標変換しましょうということです.
において2つの座標の積の項がなくなるように,座標変換しましょうということです.
 は2つの座標の2次の同次式になっていますから楕円や双曲線の回転を考えればわかるように,
は2つの座標の2次の同次式になっていますから楕円や双曲線の回転を考えればわかるように, 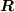 として角
として角  の回転を選ぶことができそうです.
の回転を選ぶことができそうです.
Re: 二重バネ連合
Yokkun さんのレス (2008/12/17(Wed) 20:53)
を直交座標と考えて,角
の回転
を考えましょう.
Re: 二重バネ連合
けんじ さんのレス (2008/12/17(Wed) 21:07)
(cosθ−sinθ) sinθcosθ
ですかね?
よくわかりません
問題文にヒントとして
det(xI−K)=det(R^T(xI−K)R)=(x−k1)(x−k2)
となり
k1,k2はdet(xI−K)=0となっている
と書いてありますけど…
Re: 二重バネ連合
Yokkun さんのレス (2008/12/17(Wed) 22:30)
なるほど.
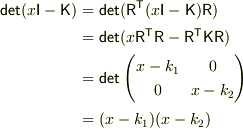 だから,
だから, 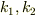 は
は
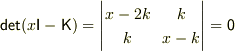 の解.そこでこれを求めてしまおうというシナリオですね.
の解.そこでこれを求めてしまおうというシナリオですね.
Re: 二重バネ連合
けんじ さんのレス (2008/12/17(Wed) 22:39)
Kは個体値であるから逆行列を持たない
よって(x−k1)(x−k2)=0
k1=k2=x?
そもそも「x」とはなんだろう またk1=xであればk2の値は何でもいいのでは?
Re: 二重バネ連合
Yokkun さんのレス (2008/12/17(Wed) 23:19)
一方
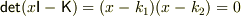 の解は,
の解は, 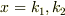 ですから,
ですから, 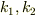 がわかったことになります.
そこで,あらためて
がわかったことになります.
そこで,あらためて
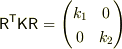 を満たす
を満たす  を導くということになります.
を導くということになります.
Re: 二重バネ連合
けんじ さんのレス (2008/12/17(Wed) 23:53)
Rの成分をa,b,c,dとおき計算しましたが,これだけ時間をかけたにもかかわらず,計算できませんでした.
ところで ・k1,k2はどのように区別されるのでしょうか(x=k1,k2 またx=(3k+k√5)/2,(3k−k√5)/2となるがどちらがk1でどちらがk2かわかりません)
・なぜここでRを導かなければならないのか
という疑問を持ちました 回答のほうをよろしくお願いします.
Re: 二重バネ連合
Yokkun さんのレス (2008/12/18(Thu) 00:15)
>k1,k2はどのように区別されるのでしょうか
多分,どちらでもいいのではないかと推測しています. Rもそれに応じた任意性を含んでいるのではないでしょうか?
>なぜここでRを導かなければならないのか
ごめんなさい.(3)で必要なのですよね?上記がOKならば(2)は終わりです.
私もやってみてますが,回転に置き換えるのはダメかもしれません. Rの直交性は明らかなので,R^T・R=Iが条件に含まれることはいいですね? 私の方は,今夜のお返事はここまでとさせていただきます.
どなたか助っ人に入って下さるとありがたいのですが・・・.
Re: 二重バネ連合
けんじ さんのレス (2008/12/18(Thu) 00:35)
Yokkunさん,回答ありがとうございました
R^TKR=(k10) 0k2
の左辺のK,右辺にそれまでに求めた値を代入して計算しましたが,Rの成分を求めることができませんでした.
だれかほかの方で教えてくださる方がいましたらよろしくお願いします.
Yokkunさん,これまでの解説ありがとうございました. わかりやすかったです.
Re: 二重バネ連合
けんじ さんのレス (2008/12/18(Thu) 01:21)
θの求め方がわかりません
(3)ですが q1,q2を用いてラグランジアンを表すと
- L=1/2m{(q1)’}^2+1/2m{(q2)’}^2
- ー1/2k1(q1)^2−1/2k2(q2)^2
となり運動方程式は
m{q1(t)}”=−k1q1 m{q2(t)}”=−k2q2
からもとめていくというのはどうでしょうか?
(なお「’」は偏微分を示しています)
Re: 二重バネ連合
けんじ さんのレス (2008/12/18(Thu) 03:39)
本日提出の課題であるのにもかかわらず,いまだに解くことができません. もうやばいです
Re: 二重バネ連合
Yokkun さんのレス (2008/12/18(Thu) 08:27)
おはようございます.
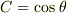 および
および 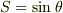 と書きます.
と書きます.
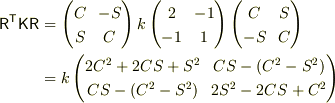 となり,
となり,
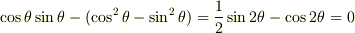 より,
より,
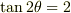 すなわち,
すなわち,
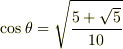
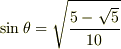 となります.また,
となります.また,
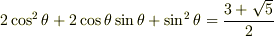
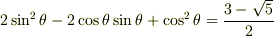 も確認できます.
運動方程式はおっしゃるとおりですね.
も確認できます.
運動方程式はおっしゃるとおりですね.
Re: 二重バネ連合
けんじ さんのレス (2008/12/18(Thu) 09:37)
おはようございます わかりやすいRの導き方ありがとうございます
運動方程式を立てたまでは良かったのですが,q1(t),q2(t)を求めるというのがわかりません
あともしかして y1(t)=q1(t)+q2(t) y2(t)=q1(t)−q2(t) ですか?
それと今日は授業があるので10時過ぎにはもう出ます すみません
Re: 二重バネ連合
Yokkun さんのレス (2008/12/18(Thu) 09:54)
>運動方程式を立てたまでは良かったのですが,q1(t),q2(t)を求めるというのがわかりません
単振動の解を書けば終わりです.
>あともしかして >y1(t)=q1(t)+q2(t) >y2(t)=q1(t)−q2(t) >ですか?
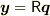 ですよね?
ですよね?
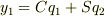
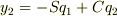 ここに,
ここに,
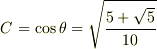
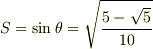 です.
なお,回転
です.
なお,回転  で対角化できるのは
で対角化できるのは  が対称な場合だけのようです.
が対称な場合だけのようです.
Re: 二重バネ連合
けんじ さんのレス (2008/12/18(Thu) 09:58)
y=Rqということを見落としていました
ところで運動方程式の解q1(t),q2(t)はどうすればいいのでしょうか?
q1(t)=−m{q1(t)}”/k1
としかわかりません
Re: 二重バネ連合
anon さんのレス (2008/12/18(Thu) 12:49)
ざっと見たところ,二次形式の標準化の問題のようですね. 線形代数の初歩的な教科書などで,「対称行列の対角化」の応用として解説が読めると思います.
Re: 二重バネ連合
けんじ さんのレス (2008/12/18(Thu) 16:20)
いま大学から帰ってきました
あのあと,自力で「B」を解きましたが,やはり間違っていましいた. やはり物理や数学の理解・発想がまだまだであると感じました
Yokkunさんには問題の解き方の手順を示していただき,本当に感謝しています
もし今後またこのようなことがありましたらよろしくお願いします.
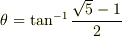 で計算があうような・・・.
で計算があうような・・・.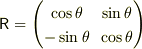 です.
です.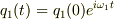 ただし,
ただし,