仕事量と運動エネルギー
仕事量と運動エネルギー
ケセラ さんの書込 (2008/12/13(Sat) 21:45)
課題が出たのですがよくわかりません.アドバイスいただけるとありがたいです.
- 問.長い糸の先に錘をつけ,多端を中心にして水平面内で回転させる.
- いま,この糸の長さを徐々に(すなわち,糸を短くしていく過程の 間でも錘の運動は円運動をしていると考えていい程ゆっくりと)短 くしていくとき,次の問に答えよ.
- (1)糸の長さがr1からr2(r2<r1)になったときの錘の速さv1,v2の比
- v2/v1を求めよ.
- (2)糸を短縮するための仕事の大きさと,錘が持っていた運動エネ
- ルギーの変化した分とを別々に求め,エネルギーの保存則の成 立することを示せ.
- (1)は自力で回答できましたが(A.v2/v1=r1/r2>1)(2)の解き方
- が分かりません.
仕事量と運動エネルギーの変化量をそれぞれ求めてそれが等しくなることを示せばいいのでしょうか? また,自分で計算してみたところ
仕事量:mv1v1{(r1r1/r2r2)-1} 運動エネルギー変化量:mv1v1/2{(r1r1/r2r2)-1}
と出ました. 運動エネルギーは正しいと思うので最終的に等しくなるなら仕事量が違うはずです.運動エネルギーは公式から,仕事量は向心力×長さで求めました. また,解答(答えのみ)には E1/v1=E2/v2 と書かれていました.最終的にこれを示すのでしょうか? お返事いただけるとありがたいです.よろしくお願いします.
Re: 仕事量と運動エネルギー
Yokkun さんのレス (2008/12/13(Sat) 22:23)
ケセラさん,こんばんは. >仕事量は向心力×長さで求めました.
向心力は回転半径とともに変わるので,積分しなければいけませんね?
>E1/v1=E2/v2 これはヒントでしょうか?E1,E2は運動エネルギーですね.
Re: 仕事量と運動エネルギー
ケセラ さんのレス (2008/12/14(Sun) 10:36)
Yokkunさんお返事ありがとうございます.
>向心力は回転半径とともに変わるので,積分しなければいけませんね?
∫mvv/r・drを積分範囲r1〜r2で積分するということでしょうか? 積分するとmvv[log|r|]となると思うのですが,これで合っているのですか?
>>E1/v1=E2/v2 これはヒントでしょうか?E1,E2は運動エネルギーですね. 問題は2問しかないはずなのですが解答には(@)〜(B)まで答えが書いてあり,(@)には(1)の答えが,(A)にはエネルギー変化量,そして(B)にE1/v1=E2/v2と書かれていました.自分でもよく意味がわからないんです.
またお返事いただけるとありがたいです.よろしくお願いします.
Re: 仕事量と運動エネルギー
ケセラ さんのレス (2008/12/14(Sun) 12:27)
mNejiさんお返事ありがとうございます.
角運動量の保存の講義は受けました. (1)で使いましたが(2)でも必要になってくるのでしょうか?
短文失礼しました.
Re: 仕事量と運動エネルギー
mNeji さんのレス (2008/12/14(Sun) 12:36)
>角運動量の保存の講義は受けました.
この問題では,外力が中心を向いた力なので,その力の経過によらず,角運動量は時間によらないで一定です,言い換えれば,運動中にその値は保存しています.
当然,外力のする仕事を計算する時にも,角運動量の保存則を適応する必要があると思います.例えば,
角運動量,L := r*mv
として,遠心力に適応することで,遠心力からvを消去する事が出来ますね.
Re: 仕事量と運動エネルギー
ケセラ さんのレス (2008/12/14(Sun) 14:42)
mNejiさんお返事ありがとうございます.
>当然,外力のする仕事を計算する時にも,角運動量の保存則を適応する必要があると思います.例えば,角運動量,L := r*mvとして,遠心力に適応することで,遠心力からvを消去する事が出来ますね.
角運動量が保存されるということは分かりましたが, 遠心力F=L/rrとしてそれを積分し,そこから仕事量を求めるということでしょうか? 間違っていたらすいません.
お返事いただけるとありがたいです.
Re: 仕事量と運動エネルギー
mNeji さんのレス (2008/12/14(Sun) 14:58)
>遠心力F=L/rrとしてそれを積分し,そこから仕事量を求めるということでしょうか?
道筋はそうだと思いますが,遠心力は,
F = (mv^2)/r
で,角運動量から
v = L/(mr)
ですから,遠心力を距離だけの関数に書けます.
F(r) = (m/r){L/(mr)}^2 = {(L^2)/m}r^{-3}
この遠心力に対抗して外力(向心力)がする仕事dW = -F(r)drですので,r1>r2と変化する時には;
W(r2) - W(r1) = -int_{r1}^{r2} F(r)dr
ではないでしょうか.
Re: 仕事量と運動エネルギー
Yokkun さんのレス (2008/12/14(Sun) 16:47)
ケセラさん,mNejiさん,こんばんは.大体解決したのかな?
はじめから整理しますと,
- 角運動量保存により
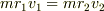
- 同様に,
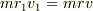 ∴
∴ 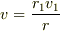
これを向心力に代入して 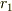 から
から 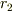 まで積分すればいいわけですね.
角運動量保存により,
まで積分すればいいわけですね.
角運動量保存により, 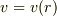 という依存関係が生じることがポイントになります.
お気づきと思いますが,符号に注意してください.
(3) 問題不明のようですが,
という依存関係が生じることがポイントになります.
お気づきと思いますが,符号に注意してください.
(3) 問題不明のようですが,
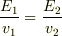
は,前後の運動エネルギー 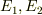 の間に成り立つ関係ですね.
の間に成り立つ関係ですね.
Re: 仕事量と運動エネルギー
ケセラ さんのレス (2008/12/14(Sun) 20:24)
mNejiさん,Yokkunさんお返事と丁寧な説明ありがとうございます. お二方のアドバイスを素に計算してみました. 計算したところ
仕事量=−(エネルギー変化量)
になりましたがこれでいいのでしょうか?(Yokkunさんの発言から考えるとOKそうですが・・・?)
Re: 仕事量と運動エネルギー
mNeji さんのレス (2008/12/14(Sun) 21:02)
>仕事量=−(エネルギー変化量)
これに付いては,設問の記述
>(2)糸を短縮するための仕事の大きさと,錘が持っていた運動エネ > ルギーの変化した分とを別々に求め,エネルギーの保存則の成 > 立することを示せ.
に注意すると,外力が遠心力にこうして,ひもを,長い半径r1から中心にむけて引っ張り,短い半径r2 で止めるまでに錘に対してする仕事 W(r1→r2)と思えます.すなわち,仕事 W(r1→r2)の値は正となります.
従って,半径r1,r2に於ける錘の運動エネルギK1, K2とすると, K1 + W(r1→r2) = K2 となります.従って,
W(r1→r2) = K2 - K1 = (運動エネルギの増分)>0.
Re: 仕事量と運動エネルギー
Yokkun さんのレス (2008/12/14(Sun) 21:42)
力の向きが,r方向と逆なことに注意してください.力が負,積分方向がrの負方向で仕事は正になるのです.
Re: 仕事量と運動エネルギー
ケセラ さんのレス (2008/12/14(Sun) 23:15)
mNejiさん,Yokkunさんお返事ありがとうございます.
お二人の説明で問題の意味は把握でき,どうにか解答できそうです.ありがとうございます. あとはこれをうまくまとめればいいのですが,仕事の計算の途中のところは
∫(r1→r2)F(r)dr
力の向きとr方向が逆なので
=LL/2m[r^(-3)](r1→r2)
という書き方でよろしいでしょうか?
お返事よろしくお願いします.
Re: 仕事量と運動エネルギー
mNeji さんのレス (2008/12/14(Sun) 23:42)
>という書き方でよろしいでしょうか?
先に書いた >F(r) = (m/r){L/(mr)}^2 = {(L^2)/m}r^{-3} >この遠心力に対抗して外力(向心力)がする仕事dW = -F(r)drですので,r1>r2と変化する時には; >W(r2) - W(r1) = -int_{r1}^{r2} F(r)dr
だと解り難い様ですので,Texで書き換えると,
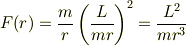
ですから,外力により糸をr1からr2に手繰り寄せる時の仕事は;
![W(r_1 \to r_2) &:= \int_{r_1}^{r_2}[-F(r)]\mathrm{d}r\\&= -\frac{L^2}{m}\int_{r_1}^{r_2}r^{-3}\mathrm{d}r\\&= -\frac{L^2}{m}\left[ \frac{r^{-2}}{-2}\right]_{r=r_1}^{r=r_2}\\&=\frac{L^2}{2m}\left( \frac{1}{r_{2}^2}-\frac{1}{r_{1}^2}\right) & \qquad \text{wheres } L=r \cdot mv \text{ for } (r,v) = (r_1, v_1), (r_2, v_2)\\&= \frac{m}{2}\left(v_2^2 -v_1^2 \right)\\&= K_2 -K_1](http://hooktail.maxwell.jp/bbslog/ef41881a56759c59b40f11efb6a24ecd.png)
となりませんか.
Re: 仕事量と運動エネルギー
ケセラ さんのレス (2008/12/15(Mon) 22:42)
Yokkunさん,mNejiさんお返事ありがとうございます. お2人の分かりやすい説明で無事に解答できました. 本当にありがとうございました.
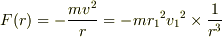 とするのが簡明だと思います.
これを
とするのが簡明だと思います.
これを