放物運動

放物運動

Yokkun さんの書込 (2008/12/13(Sat) 18:46)

放物運動の初歩的な問題です． 地上高 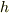h の地点から初速 v で物体を投射するとき，投射地点直下からの水平到達距離 L を最大とする投射角 \theta （仰角）を求めよ．ただし，空気抵抗は無視できるものとする．

という問題で，微積分および物理いずれの演習書を見ても, L を単純に \theta で微分する下記のシナリオによる解法でした．解答の単純さを見ると何か他のブレイクスルーがありそうな気がするのですが，どうなのでしょう？

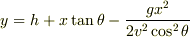
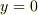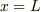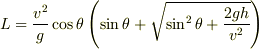
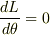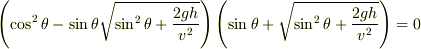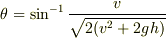軌道は， y=h+x\tan\theta-\frac{gx^2}{2v^2\cos^2\theta} y=0 のとき， x=L により L の2次方程式を解くと， L&=\frac{v^2}{g}\cos\theta\left(\sin\theta+\sqrt{\sin^2\theta+\frac{2gh}{v^2}}\right) \frac{dL}{d\theta}=0 によりちょっとした計算の後に， \left(\cos^2\theta-\sin\theta\sqrt{\sin^2\theta+\frac{2gh}{v^2}}\right)\left(\sin\theta+\sqrt{\sin^2\theta+\frac{2gh}{v^2}}\right)=0 となり， \theta=\sin^{-1}\frac{v}{\sqrt{2(v^2+2gh)}} を得る．