波動関数のグラフ

ヤグさんの書込 (2008/12/09(Tue) 23:26)

初めまして．大学のレポートで丸2日間苦しんでおります，教えて下さい．

問題は，

直線を運動する粒子の波動関数が

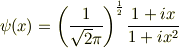
$\psi(x)=\left(\frac{1}{\sqrt{2}\pi}\right)^{\frac{1}{2}}\frac{1+ix}{1+ix^{2}}$

で与えられるとき，確率分布 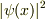$|\psi(x)|^{2}$ のグラフを描け．また，存在確率密度がもっとも大きい点はどこか．

です．

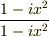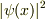与えられた波動関数に $\frac{1-ix^{2}}{1-ix^{2}}$ を掛けてその後， $|\psi(x)|^{2}$ でiを消去し，式変形を行って

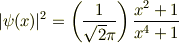
$|\psi(x)|^{2}=\left(\frac{1}{\sqrt{2}\pi}\right)\frac{x^{2}+1}{x^{4}+1}$

まで出来ましたが，そこでつまずいて動けません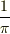． $\frac{1}{\pi}$ があるのでローレンツ分布(コーシー分布)だと思うのですが…．

どうぞ，よろしくお願い致します．

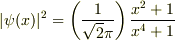> $|\psi(x)|^{2}=\left(\frac{1}{\sqrt{2}\pi}\right)\frac{x^{2}+1}{x^{4}+1}$ まで出来ましたが，そこでつまずいて動けません．

???

ここまでできたら，後は何も障害はないでしょう? gnuplotなどでグラフを書けば「ふたこぶ」のグラフが得られます．存在確率密度がもっとも大きい点は，極値になる点を求めればよいですね．(高校数学の範囲です．)

Hiroさん

そうですね．無理矢理にローレンツ分布の定義式の形に変形しなければいけないと勘違いしていました．無事に解く事ができました．ありがとうございました．