エントロピー
エントロピー
じょけr さんの書込 (2008/12/08(Mon) 20:24)
エントロピーについていろいろな本を読みましたが, 理解できません.クラウジウス積分が出てきたあたりから, わからなくなりました. Qは状態量ではないのに,それをTで割ることで状態量になるのが 納得いきません. また,この物理量の有用性がわかりません
Re: エントロピー
mNeji さんのレス (2008/12/08(Mon) 23:28)
丁度,ある本で1階1次の微分方程式;
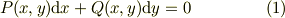
の解を求める話を拝見したところでした.
もし,左辺がある関数 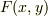 の全微分で表せたとすれば,
の全微分で表せたとすれば,
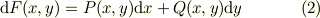
ですから,式(1)より,微分方程式の解は,
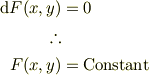
となります.
一方,関数の全微分を展開して,
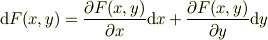
となるので,式(2)と比較して,
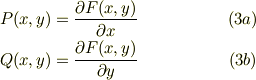
という関係が成り立つ必要がある.
式(3a)をyで偏微分し,式(3b)をxで偏微分すると,偏微分の順序を交換してもよいことから,
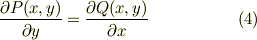
の関係が積分可能条件となる.
他方,式(4)が成立しない場合でも,微分方程式(1)にある関数 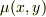 を掛ける事で,
を掛ける事で,
![\mu(x,y) [P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y] = \mathrm{d}G(x,y) =0 &(5)](http://hooktail.maxwell.jp/bbslog/1c207405b02572089af8d6ec5723f745.png)
と出来る場合がある.このとき, 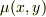 を積分因子(integrating factor)と呼ばれる.式(5)が成立する必要十分条件は,式(4)と同様に,積分可能条件,
を積分因子(integrating factor)と呼ばれる.式(5)が成立する必要十分条件は,式(4)と同様に,積分可能条件,
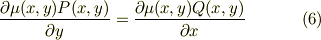
となる.
式(5)の右辺・関数Gの全微分から,
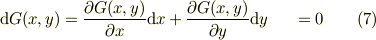
と,式(5)の左辺を比較して,積分因子は,
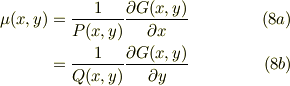
となる....そうです.
出典:下記のpp44-45. 理工系の基礎数学10 微分・位相幾何 和達 三樹・著 岩波書店,1996 ISBN4-00-007980-8
Re: エントロピー
toorisugari no Hiro さんのレス (2008/12/10(Wed) 19:16)
じょけrさんが求める回答ではないのですが,積分因子の話が出たので,その関連の数学の話.
ある1形式  が適当な積分因子で割ることで全微分になるとは,
が適当な積分因子で割ることで全微分になるとは,
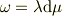
という形である事は自明ですね.上の形式をcomplex lamellar(複層?)といいます. このとき,
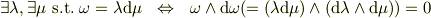
が成り立ちます. # 通常の3次元ベクトル解析の言葉で書くと
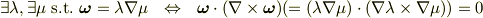
です.
第一法則から
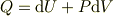
ですので
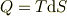
となる 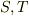 が存在するためには
が存在するためには
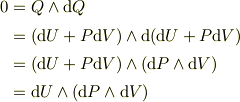
である必要があり,これは  が
が 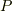 と
と  の関数であるということです.
の関数であるということです.
質量のやりとりのない準静可逆過程において,その空間は2次元であり,圧力と体積を指定すれば状態が決まります(カルノーサイクルのグラフの縦軸と横軸はそれぞれ圧力と体積ですね).故に,
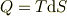
となる 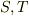 が存在します.
が存在します.
# なお,2次元の任意の1形式 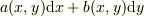 (or
(or 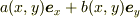 )はcomplex lamellarであることは容易に分かりますね.
)はcomplex lamellarであることは容易に分かりますね.