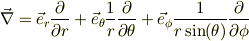極座標表現

極座標表現

まー さんの書込 (2008/12/07(Sun) 12:35)

こんにちは＾＾ 極座標（ｒ，θ，φ）について∇（∂/∂ｒ，∂/∂θ，∂/∂φ）をそれぞれの座標表現で求めるときは，どうすればいいですか？

いろいろ調べたんですが調べているうちにナブラとかいろいろごちゃごちゃになってわからなくなってしまいまして・・

お願いします．

Re: 極座標表現

mNeji さんのレス (2008/12/07(Sun) 16:12)

まーさん，あまり厳密でない説明をしてみたいと思います．

まず，1次元の関数f(x)があったとして，その微分を考えます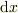．「 \mathrm{d}x 」が十分に微量ならテイラー展開の1次の項までで表せて，

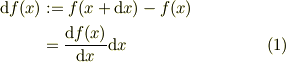
\mathrm{d}f(x)&:= f(x+\mathrm{d}x) -f(x)\\&= \frac{\mathrm{d}f(x)}{\mathrm{d} x}\mathrm{d}x &(1)

いま，x軸について，「座標値x」の増える方向に単位ヴェクタ 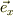\vec e_x を考えると，「座標値x」の点の座標ヴェクタ 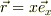\vec r = x\vec e_x と書けます．また単位ヴェクタの為に，その内積 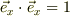\vec e_x\cdot \vec e_x =1 に注意すれば，

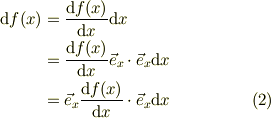
\mathrm{d}f(x)&= \frac{\mathrm{d}f(x)}{\mathrm{d} x}\mathrm{d}x\\&= \frac{\mathrm{d}f(x)}{\mathrm{d} x}\vec e_x \cdot \vec e_x \mathrm{d}x\\&= { \vec e_x \frac{\mathrm{d}f(x)}{\mathrm{d} x}} \cdot \vec e_x \mathrm{d}x &(2)

そこで，一次元ヴェクタ演算子 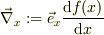\vec \nabla_x := \vec e_x\frac{\mathrm{d}f(x)}{\mathrm{d} x} と，位置のヴェクタの微分(微小変位) 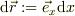\mathrm{d}\vec r := \vec e_x\mathrm{d}x とすれば，関数の微分はヴェクタ表現として，

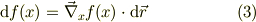
\mathrm{d}f(x) &= \vec \nabla_x f(x)\cdot \mathrm{d}\vec r &(3)

となります．

式(3)は，1次元から3次元デカルト座標には容易に拡張されて，

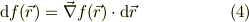
\mathrm{d}f(\vec r) &= \vec \nabla f(\vec r)\cdot \mathrm{d}\vec r &(4)

となる訳でした．ですから，勾配ヴェクタ演算子の任意座標系での表現は，位置座標の微分ヴェクタとその基底ヴェクタが決まれば，「式(4)が成り立つ様に決まる」と考える事ができます．

そこで，極座標 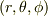(r,\theta,\phi) での表現を求めてみます．

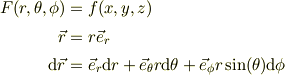
F(r,\theta,\phi) &=f(x,y,z)\\\vec r &= r\vec e_r\\\mathrm{d}\vec r &= \vec e_r \mathrm{d}r + \vec e_{\theta} r\mathrm{d}\theta +\vec e_{\phi} r\sin(\theta)\mathrm{d}\phi

従って関数 F(r,\theta,\phi) の全微分は，基底ヴェクタが単位直交である事を利用すると，下記の様に変形出来る；

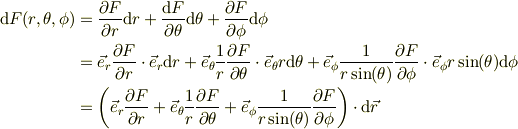
\mathrm{d}F(r,\theta,\phi) &= \frac{\partial F}{\partial r}\mathrm{d}r+\frac{\mathrm{d}F}{\partial \theta}\mathrm{d}\theta+\frac{\partial F}{\partial \phi}\mathrm{d}\phi\\&= \vec e_r \frac{\partial F}{\partial r}\cdot \vec e_r \mathrm{d}r+ \vec e_{\theta}\frac{1}{r}\frac{\partial F}{\partial \theta}\cdot \vec e_{\theta} r\mathrm{d}\theta+\vec e_{\phi}\frac{1}{r\sin(\theta)} \frac{\partial F}{\partial \phi}\cdot \vec e_{\phi} r\sin(\theta)\mathrm{d}\phi\\&= \left( \vec e_r \frac{\partial F}{\partial r}+\vec e_{\theta}\frac{1}{r}\frac{\partial F}{\partial \theta}+\vec e_{\phi}\frac{1}{r\sin(\theta)} \frac{\partial F}{\partial \phi}\right) \cdot \mathrm{d}\vec r

これを式(4)と比較して

\vec \nabla = \vec e_r \frac{\partial }{\partial r}+\vec e_{\theta}\frac{1}{r}\frac{\partial }{\partial \theta}+\vec e_{\phi}\frac{1}{r\sin(\theta)} \frac{\partial }{\partial \phi}

Re: 極座標表現

まー さんのレス (2008/12/08(Mon) 13:41)

なるほど！(^^) 一次元の関数からの説明までご丁寧にしてくれたので とてもわかりやすかったです． ありがとうございます☆彡