重力波放射の計算

トビラ．．さんの書込 (2008/12/07(Sun) 00:32)

こんばんわ．すみません色々計算の仕方をためしたのですがどれもうまくいかず，とてつもなくギブアップなので，どうかアドバイスお願いします（ちょっとしたヒントでもいいので）．まず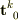， $\mathbf t^k_{\,\,\,0}$ を

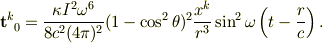
$\mathbf t^k_{\,\,\,0}=\frac{\kappa I^2 \omega^6}{8c^2 (4\pi)^2}(1-\cos ^2\theta)^2\frac{x^k}{r^3}\sin^2\omega\left( t-\frac{r}{c}\right).$

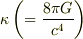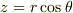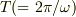として，ここで， $\kappa \left(=\displaystyle\frac{8\pi G}{c^4}\right)$ はEinstein定数．は光速度． $\theta$ は -軸との角度で $z=r\cos \theta$ という関係があります．また，角振動数 $\omega$ の周期を $T(=2\pi/\omega)$ として，さらに面積素片を 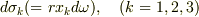$d\sigma_k(=rx_k d\omega),\quad (k=1,2,3)$ とすると

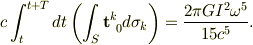
$c\int^{t+T}_{t}dt\left( \int_S \mathbf t^k_{\,\,\,0} d\sigma_k\right)=\frac{2\pi GI^2\omega^5}{15c^5}.$

となるそうなのですが，どのように計算すればこの右辺になるのでしょうか？とくに 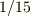1/15 という係数になる理由が皆目見当も付きません．ヒントでいいのでどうか，教えてください．お願いします．

Re: 重力波放射の計算

Yokkun さんのレス (2008/12/07(Sun) 10:52)

トビラ．．さん，こんにちは．

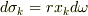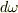とてもお役に立てそうにはないのですが，興味がありますので．・・・で確認ですが， $d\sigma_k=rx_kd\omega$ の $d\omega$ は角振動数 $\omega$ とは違いますよね？

Re: 重力波放射の計算

mNeji さんのレス (2008/12/07(Sun) 18:36)

ちゃちゃです：てっきり球状重力源の動径方向の振動が最低次のモードだとおもっていましたが，四重極モーメントみたいな感じですかねぇ．

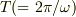私も，＞角振動数 $\omega$ の周期を $T(=2\pi/\omega)$ として，さらに面積素片を 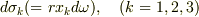$d\sigma_k(=rx_k d\omega),\quad (k=1,2,3)$ とすると

とすると，なんか定義が？，のように感じます．前者が角振動数なら，後者は立体角のように思います．そうなら後者を 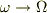$\omega \to \Omega$ とするとか．

Re: 重力波放射の計算

Yokkun さんのレス (2008/12/07(Sun) 18:52)

mNejiさん，こんばんは．

mNejiさんの推測が当たっているようです．手元にあるテキストを見ると，４重極子による重力波が単位時間に運ぶエネルギーの結果に一致します．すると，全立体角について積分すればいいようですね．

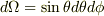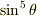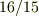$d\Omega=\sin\theta d\theta d\phi$ でうまくいきました． $\sin^5\theta$ の積分が 16/15 になります．

Re: 重力波放射の計算

なんとなくさんのレス (2008/12/07(Sun) 19:45)

私もちゃちゃですが．重力波の場合，極性がないのでダイポールは無く，四重極が最低次のエネルギーではなかったですかね．計算はYokkunさんの言うとおり，結局ガウスの定理により単位時間に放出されるエネルギー（の時間平均）なのでしょうね．遅延波を使っていますが，半径ｒに拠らないこと（当たり前ですが）が見て取れますね．ヒントはもう明白ですが，極座標で計算すれば簡単ですね．

Re: 重力波放射の計算

トビラ．．さんのレス (2008/12/07(Sun) 23:09)

＞トビラ．．さん，こんにちは．

こんにちわ．

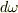＞ $d\omega$ は角振動数 $\omega$ とは違いますよね

まじっ？（汗）ちっ・・・違うんですか・・・思いっきり同じものだと思ってました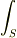． $\int_S$ という表面積分なのに角振動数 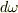$d\omega$ で積分域をどうやって決めようか悩んでいました．

＞とてもお役に立てそうにはないのですが

僕にとってはこれだけで大きな前進なんですけども・・・（笑）

Yokkunさん，mNeji師匠！，なんとなくさん，どうもありがとうございました．皆さんのアドバイスをふまえてもう一度計算をしてみます．ありがとうございました．

Re: 重力波放射の計算

Yokkun さんのレス (2008/12/08(Mon) 02:20)

何かお役に立ってしまいました． mNejiさん，なんとなくさん，バックアップありがとうございました．

Re: 重力波放射の計算

トビラ．．さんのレス (2008/12/09(Tue) 23:01)

返事遅れてすみません．おかげさまで解けました．一応，感謝の気持ちとして計算のせておきます．（おせわになったので）

球の表面積を計算するので，極座標が便利である．よって，体積素片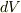は

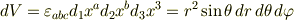
$dV=\varepsilon_{abc}d_1 x^ad_2x^bd_3x^3=r^2\sin\theta \,dr\,d\theta\,d\varphi$

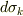なので，面積素片 $d\sigma_k$ は

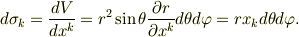
$d\sigma_k=\frac{dV}{dx^k}=r^2\sin\theta\frac{\partial r}{\partial x^k}d\theta d\varphi=rx_k d\theta d\varphi.$

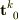これを使って， $\mathbf t^k_{\,\,\, 0}$ を表面積分すると

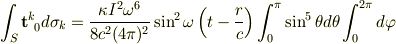
$\int_S \mathbf t^k_{\,\,\, 0}d\sigma_k=\frac{\kappa I^2 \omega^6}{8c^2 (4 \pi)^2}\sin^2\omega\left( t-\frac{r}{c}\right)\int^\pi_0 \sin^5\theta d\theta \int^{2\pi}_0d\varphi$

ここで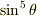， $\sin^5\theta$ の積分は

$\int^\pi_0\sin^5\theta d\theta=\int^\pi_0(1-\cos^2\theta)^2\cdot \sin\theta d\theta=\int^\pi_0 \left\{ \sin\theta+2\cos^2\theta(-\cos\theta)^\prime-\cos^4\theta(-\cos\theta)^\prime\right\}d\theta=\left[-\cos\theta +\frac{2}{3}\cos^3\theta-\frac{1}{5}\cos^5\theta\right]^\pi_0=\frac{16}{15}$

また，

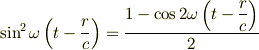
$\sin^2\omega \left( t-\frac{r}{c}\right)=\displaystyle\frac{1-\cos 2\omega\left(t-\displaystyle\frac{r}{c}\right)}{2}$

なので，この式を使うと簡単な積分の後に

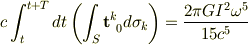
$c\int^{t+T}_{t}dt\left( \int_S\mathbf t^k_{\,\,\, 0}d\sigma_k\right)=\frac{2\pi GI^2 \omega^5}{15 c^5}$

ともとまる．です．（多分これであってる．証明が雑だけども・・・） Yokkunさん，mNejiさん，なんとなくさん，トビラ．．さ・・・あ僕か・・・どうもありがとうございました．大変助かりました．

[home] [掲示板] [ページの先頭]