共変微分による極座標系ラプラシアンの導出
共変微分による極座標系ラプラシアンの導出
ファイル さんの書込 (2008/11/30(Sun) 21:52)
問題の質問というよりは,自分の個人的な興味で考えたものを見ていただきたいのですが・・・. お暇なら見てください.
相対論で座標変換を勉強していて,それを応用して何とか,あの複雑な極座標のラプラシアンを導出できないかと考えていました. そもそも,なぜラプラシアンがあのような複雑な形になるのかというと,極座標の基底が一定でないから,というのが原因だと思います. その基底の変化も考慮したのが,共変微分であり,基底微分の項はクリストッフェル記号で表されます.さらに,クリストッフェル記号はメトリックで表されるので,最終的には極座標のメトリックだけから計算できることになります.
添え字は 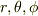 の三つを表すものとします.
極座標のメトリックは,
の三つを表すものとします.
極座標のメトリックは,
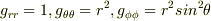 というのは,極座標の基底をデカルト座標の基底で展開した式からも簡単に計算できますし,微小線素を描いて直観的に求めることも出来ると思います.
それで,発散
というのは,極座標の基底をデカルト座標の基底で展開した式からも簡単に計算できますし,微小線素を描いて直観的に求めることも出来ると思います.
それで,発散 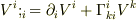 の式にあるクリストッフェル記号を求めれば良いと思うのですが,全部で9つのクリストッフェル記号を求める必要があり,これが結構大変です.
クリストッフェル記号とメトリックの関係式において,メトリックが対角成分しか持たないことに着目すると,割と簡単な式になり
の式にあるクリストッフェル記号を求めれば良いと思うのですが,全部で9つのクリストッフェル記号を求める必要があり,これが結構大変です.
クリストッフェル記号とメトリックの関係式において,メトリックが対角成分しか持たないことに着目すると,割と簡単な式になり
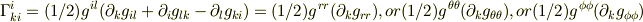
となります.
これを9つの成分について計算すると,ほとんどがゼロとなって
結局
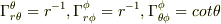 だけが残りました.
これを
だけが残りました.
これを
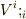 の式に代入すると,発散は
の式に代入すると,発散は
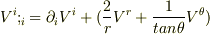 となります.
となります.
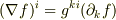 によって計算した勾配
によって計算した勾配
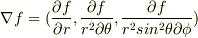 を発散の式の
を発散の式の 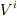 に代入すると,なんとか極座標のラプラシアンを導くことが出来ました.
に代入すると,なんとか極座標のラプラシアンを導くことが出来ました.
一年生のときにならった単純に計算する方法よりは簡単に導出できるかと思いますが,クリストッフェル記号を9つ計算しなければならないところが気になっています. もし,対称性などを利用してゼロになる成分を見つける方法や,計算の手間を省く方法, あるいは,より簡単に極座標のラプラシアンを導出する良い方法などがありましたら教えていただきたいです.
(そもそもラプラシアンなんて導出しなくても,教科書をみればいいのだ,とは思いますが,数学の練習だと思ってやってみました.)
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/01(Mon) 10:17)
ファイルさん,こんにちは.たいへん教育的な意義のある計算になりますね.もちろん,一般座標に一気に駆け上った後にユークリッド空間の極座標に降りてくるのですから,理論的にはずいぶんな遠回りですが,クリストッフェル記号や共変微分というツールが身についていることを前提すれば,より簡略な導出といえるでしょうか?^^;
この分野に関していうならファイルさんの学びが私よりずっと先をいっていると思われるので,割引して聞いてくださいね.
接続係数(クリストッフェル記号)の基礎的な理解の際に出てくる平行移動の概念が少し役に立つかなあと思います.
平行移動によって生じるベクトル成分の変化は,
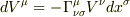 となるわけですが,これは
となるわけですが,これは
 方向への平行移動
方向への平行移動 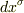 によって生じる
によって生じる 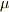 成分の変化率を
成分の変化率を  成分の1次結合で表す係数,いいかえれば
成分の1次結合で表す係数,いいかえれば 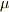 成分変化の
成分変化の  成分依存性を表す・・・ということになるかと思います.表現上正確でないかもしれない部分は勘弁してください.
成分依存性を表す・・・ということになるかと思います.表現上正確でないかもしれない部分は勘弁してください.
すると,極座標上の平行移動において,微小体積要素の大きさと方向がどう変わるかを考えれば,生き残るクリストッフェル記号を拾いあげることができます.必ずしも簡明ではないのでお役に立つかわかりませんが,
(1) r方向への平行移動
θ,φ方向への拡大・縮小
θ成分の変化→θ成分に依存→ 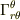 φ成分の変化→φ成分に依存→
φ成分の変化→φ成分に依存→ 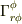 (2) θ方向への平行移動
φ方向への拡大・縮小
φ成分の変化→φ成分に依存→
(2) θ方向への平行移動
φ方向への拡大・縮小
φ成分の変化→φ成分に依存→ 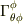 φ方向まわりの回転
r成分の変化→θ成分に依存→
φ方向まわりの回転
r成分の変化→θ成分に依存→ 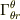 θ成分の変化→r成分に依存→
θ成分の変化→r成分に依存→ 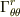 (3) φ方向への平行移動
θ方向まわりの回転
r成分の変化→φ成分に依存→
(3) φ方向への平行移動
θ方向まわりの回転
r成分の変化→φ成分に依存→ 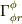 φ成分の変化→r成分に依存→
φ成分の変化→r成分に依存→ 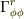 r方向まわりの回転
θ成分の変化→φ成分に依存→
r方向まわりの回転
θ成分の変化→φ成分に依存→ 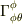 φ成分の変化→θ成分に依存→
φ成分の変化→θ成分に依存→ 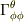 以上が生き残ることがわかります.
※下付添え字が逆になりましたが,対称ですからお見逃しを.
以上が生き残ることがわかります.
※下付添え字が逆になりましたが,対称ですからお見逃しを.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/01(Mon) 12:01)
ラプラシアンの計算の仕方は No.22219 で触れています.ここでは正規直交基底で計算していますが,自然基底で計算すれば,
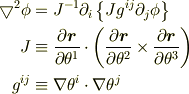
が得られるはずです.
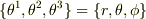 とすれば良いですね.
とすれば良いですね.
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/01(Mon) 14:45)
えーと,ちょっとカンニングしてきました.
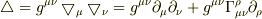 ここに,
ここに,
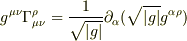 を適用して,
を適用して,
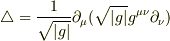 これのことですね?>toorisugari no Hiro さん.
ずいぶんコンパクトになっちゃったですね.展開も簡単にできました.
これのことですね?>toorisugari no Hiro さん.
ずいぶんコンパクトになっちゃったですね.展開も簡単にできました.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/01(Mon) 14:51)
> これのことですね?>toorisugari no Hiro さん.
はい.そうです.
# 私はまだ接続を使った計算には慣れていませんので,Yokkunさんのやり方は苦手ですが...
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/01(Mon) 14:56)
一般座標系におけるラプラシアンの導出は,接続を使った方が遙かに短くできますが,参考のため使わずに出します. No.22219の改訂版です.
今,曲線座標系 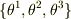 を考えます.
を考えます.
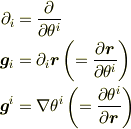
として,変位ベクトルとナブラ,及び体積要素は,
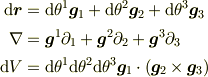
と書けます.
ここで
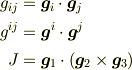
と定義します.
# 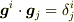 は定義より明らかですね.
は定義より明らかですね.
ベクトル解析の公式
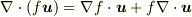 を既知とすると,
を既知とすると,
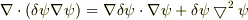 が得られるので,
が得られるので, 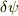 を境界で消える任意関数として,ガウスの発散定理により,
を境界で消える任意関数として,ガウスの発散定理により,
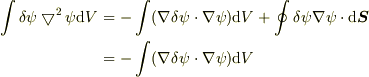 (グリーンの定理もどき)が得られます.
# これをラプラシアンの定義と考えても良いです.(注*)
(グリーンの定理もどき)が得られます.
# これをラプラシアンの定義と考えても良いです.(注*)
右辺を成分で計算し,(境界積分は0として)部分積分を行えば,左辺の成分表示が得られます. 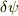 は任意関数ですから,これより,ラプラシアンの成分表示が得られます.
は任意関数ですから,これより,ラプラシアンの成分表示が得られます.
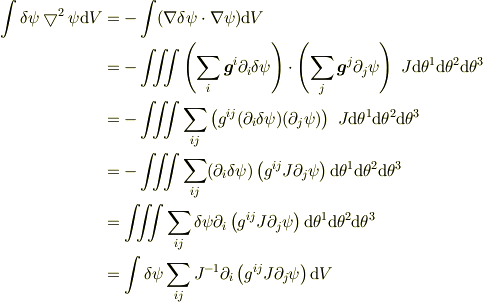
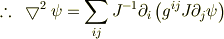
# 注*)あるいはLaplacianを以下の汎関数
![I[\psi] &= -\frac{1}{2}\int |\nabla \psi|^2 \mathrm{d}V](http://hooktail.maxwell.jp/bbslog/edc4c20ce234edad285ba351d2e53093.png)
の変分
![\bigtriangledown^2\psi(x) &\equiv \frac{\delta I[\psi]}{\delta \psi(x)}](http://hooktail.maxwell.jp/bbslog/0a21f691ea9010a2bc3714c0f027bd19.png)
で定義する方がより一般的で良いです. # 具体的な計算手順は変わりません.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/01(Mon) 18:45)
ついでですから,ここで「問題の丸投げ」をさせてください.:-) スカラーに対するラプラシアンは
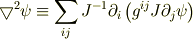
と書けます. ではベクトルに対するラプラシアン
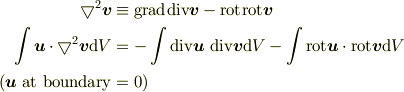
はどう書けるのでしょう.
ベクトルに対しても,成分をスカラと見なしてスカララプラシアンを作用させる演算子を 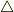 で表す
で表す
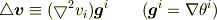
とすれば,
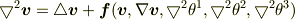
の様な形にできるのではないかと,重力波の「調和座標系」の議論から予想しているのですが,計算が.....
# きっと電磁波の伝搬を扱う分野では,古くからある議論だと思うので,文献があれば教えてください.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/02(Tue) 11:43)
> ![[\bigtriangleup\bm{v}]^i = \partial^j\partial_jv^i](http://hooktail.maxwell.jp/bbslog/af6a7f26cf8c4270560c8576b7671848.png) (
( 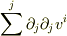 と書くべきかな?)
ということですよね?
と書くべきかな?)
ということですよね?
![[\bigtriangleup \bm{v}]^i &\equiv \sum_{mn} J^{-1} \partial_m \left( g^{mn} J \partial_n v^i \right)](http://hooktail.maxwell.jp/bbslog/a9f1c8f0c1149deb0048d0a1a08b66b0.png) です.
# のつもりでしたが,下の調和条件を考えるとYokkunさんの前者のほうでいいようです.
です.
# のつもりでしたが,下の調和条件を考えるとYokkunさんの前者のほうでいいようです.
あと,
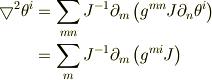
ですから,座標関数が調和的( 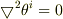 )という条件が
)という条件が
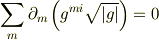
となり,これを満たす「調和座標系」では
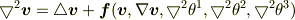
の 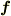 が消えると予想してるのですが.
が消えると予想してるのですが.
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/02(Tue) 14:50)
ベクトルにラプラシアンを作用させると・・・
ここで調和条件を適用すると,第2項が消えて
![g^{ij}\bigtriangledown_i\bigtriangledown_j v^k &= g^{ij}[\partial_i\partial_j v^k+\partial_i\Gamma^k_{jm}\cdot v^m+\Gamma^k_{jm}\partial_i v^m+\Gamma^k_{im}\partial_j v^m+\Gamma^k_{im}\Gamma^m_{jn}v^n]](http://hooktail.maxwell.jp/bbslog/dd5fa68274b8dee06bbaec552fa3e91f.png)
てな具合になるように思うのですが.曲率ゼロを仮定するとさらに進みそうな形はしています.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/02(Tue) 16:55)
Yokkunさんありがとうございます. 私もやってみました.
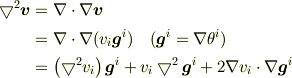
となりました.
第1項,第2項は予想通りですが,第3項は調和条件ではきえそうにありませんね.
ちなみに,第3項は 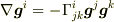 より
より
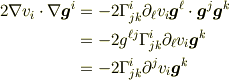
第2項は
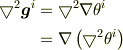
です.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/03(Wed) 12:25)
> この第2項も消えるということになるわけで・・・.
たぶん,そう簡単に消えないと思います.私がやったのは

で,これは1-formのラプラシアン
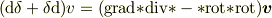
にあたりますが(  はホッジ双対),
はホッジ双対),
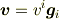
という展開は1-vectorに相当し,形式と対応づけるなら,1-formに書き換えるか,
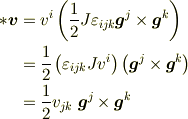
と,2-form(あるいは反対称共変テンソル)としなければきれいな形にならないからです.(ユークリッド空間では 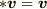 です.)
# 2-formのラプラシアンは
です.)
# 2-formのラプラシアンは
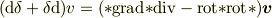
と形もすこし違っています.
2-formの具体的な計算は...行き詰まってます.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/03(Wed) 13:01)
> 曲率ゼロを仮定するとさらに進みそうな形はしています.
どうなんでしょう.曲率が議論にはいるとおもしろいですが,ラプラシアンは対称なので曲率は出てこない気がします.
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/03(Wed) 13:57)
うひゃー.やはり,Hiroさんの方法論はハナから微分形式なんですね.鉛筆のかわりに頭を使うやつ・・・.*が微分演算子とともに出てきた時点で,私はノックアウトです.マクスウェル方程式の簡素化にあたっては,感動した記憶がありますが.
ところで,重力波の議論ではダランベルシアンの対象が計量テンソルそのものなのですが,調和条件の形はそれと即応しているわけではないのでしょうか?
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/03(Wed) 14:30)
> Hiroさんの方法論はハナから微分形式なんですね.
いえ,自然座標系+ベクトル解析が基本で,そこに微分形式の香りがあるかなという程度.接続,曲率,微分形式,まだよく理解していません.
> *が微分演算子とともに出てきた時点で,私はノックアウトです.
ホッジ双対といってもユークリッド空間では
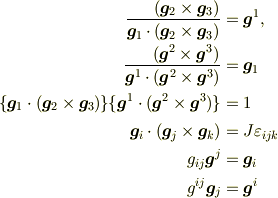
という公式群にすぎません(第一式は両辺に 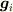 で内積をとって
で内積をとって 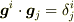 を考慮する) .
を考慮する) .
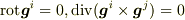 を考慮して計算が楽になる基底に変換(
を考慮して計算が楽になる基底に変換( 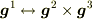 )するという使い方です.
)するという使い方です.
> 重力波の議論ではダランベルシアンの対象が計量テンソルそのものなのですが,調和条件の形はそれと即応しているわけではないのでしょうか?
えっと,ですね.ここ分からなくなっているですが,
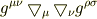
ってそもそも0ですよね.
 って
って 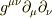 ,それとも
,それとも 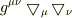 でしたっけ.
でしたっけ.
Re: 共変微分による極座標系ラプラシアンの導出
ファイル さんのレス (2008/12/03(Wed) 15:42)
Yokkunさん,toorisugari no Hiroありがとうございます. お二人のお話はレベルが高すぎて,私にはついていけませんが,No.22384の表記がとても分かりやすくて満足しました. クリストッフェル記号をメトリックの行列式で表せば,わざわざ9つの成分を計算する必要はなかったですね.概念的にもメトリックだけからラプラシアンが計算されるのが一目瞭然で理解しやすいです.
みなさんの専攻は数学・・・ではないですよね^^; 前回,toorisugari no Hiroさんにご紹介していただいた数学の本を読んでみようと思うのですが,まだまだ先は長そうです.
#Yokkunさん,No.22384の式の添え字についてですが,ラプラシアンの第二項目は
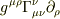 ではないですか?
発散のところで,クリストッフェル記号の縮約が出てくると思います.
クリストッフェルの縮約を計算すると二式目の
ではないですか?
発散のところで,クリストッフェル記号の縮約が出てくると思います.
クリストッフェルの縮約を計算すると二式目の 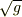 を含む式が出てくるので,結果は同じになりますが.
を含む式が出てくるので,結果は同じになりますが.
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/03(Wed) 15:46)
えーと,カンニング.
Diracの訳書で, 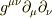 となっています.一貫性を欠くようですが,もともとゼロなら波動を表すことになりませんものね?^^; からっぽの空間の「弱い」重力場を調和座標で記述することでダランベールの方程式が成立するということになっています.
となっています.一貫性を欠くようですが,もともとゼロなら波動を表すことになりませんものね?^^; からっぽの空間の「弱い」重力場を調和座標で記述することでダランベールの方程式が成立するということになっています.
えーと.ファイルさんどうも.
私はここもカンニングしたのでよくわかりませんが,むしろ符号が気になっています.
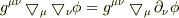
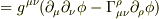 と考えたのですが,ファイルさん助けてください.
と考えたのですが,ファイルさん助けてください.
Re: 共変微分による極座標系ラプラシアンの導出
ファイル さんのレス (2008/12/03(Wed) 17:44)
私は,まだ共変微分を勉強したばかりで,ぜんぜん慣れてないんですw
>私はここもカンニングしたのでよくわかりませんが,むしろ符号が気になっています. 符号はマイナスであってると思います. すみません,さっきの「添え字間違ってませんか?」は私のカンチガイでした.
私は,メトリックを共変微分の中に入れてしまって, 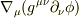 として計算しました.
つまり,ベクトルの共変微分と見たので
として計算しました.
つまり,ベクトルの共変微分と見たので
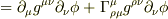 となります.
となります.
Yokkunさんは,メトリックを外に出したまま計算,つまり双対ベクトルの共変微分と見て,計算したのだと思います.
ところで,私の式ですが,第一項目の偏微分を計算すると
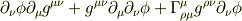
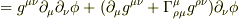 になります.
ところで,メトリックの共変微分は
になります.
ところで,メトリックの共変微分は
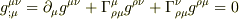 ですから
この式を上の式のカッコのなかに代入すると
ですから
この式を上の式のカッコのなかに代入すると
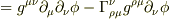 となって
Yokkunさんの式と一致します.
となって
Yokkunさんの式と一致します.
つまり,私の式もYokkunさんの式も同じものでした. たいへん失礼しました.ごめんなさい.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/03(Wed) 18:00)
苦闘してました.
> メトリックの共変微分は |44cb016878455e07eba20d618f7d2116| ですから
なるほど.
ついでに
> ここに,
> 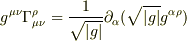
も導出してくれます?
Re: 共変微分による極座標系ラプラシアンの導出
ファイル さんのレス (2008/12/03(Wed) 19:42)
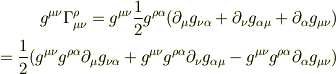
ここで,二項目の 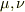 の添え字を入れ替ると,
の添え字を入れ替ると,
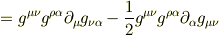
また,メトリックの偏微分に関する公式
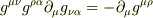
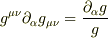 を使うと
を使うと
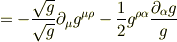
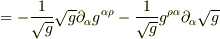
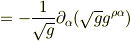
となりました. 途中で使ったメトリックの微分公式は,本に載っていたものをそのまま使いました. 私はよく意味がわからないのですが,相対論の計算ではたまに出てくる公式のようです. あと,なぜかマイナス符号が出てきてしまいました. 計算間違いしてるかもしれません. さきにクリストッフェル記号の縮約を計算したものにメトリックをかけたほうが計算量は減ると思います.(結果は同じですが.)
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/03(Wed) 20:37)
>あと,なぜかマイナス符号が出てきてしまいました.
さっきのマイナスと相殺して,うまくいくようです. 私のカンニング先の問題でしょう.クリストッフェルの符号が逆に定義されているのかも・・・.
第1式
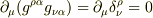 一方,
一方,
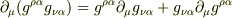 ∴
∴ 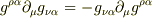 両辺に
両辺に 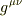 をかけて,
をかけて,
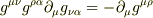
Re: 共変微分による極座標系ラプラシアンの導出
ファイル さんのレス (2008/12/03(Wed) 21:00)
そうですか,よかったです. この分野は,定義が本によって違ったり,添え字の文字がバラバラだったりで大変ですね.
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/03(Wed) 21:21)
そうなんですよね.はじめのころは,計量の符号にもずいぶんとまどいました.>ファイルさん
第2式
レビ・チビタ使いたくないので,エレガントでありませんが初歩的にやらせてください.ひとまずアインシュタイン規則解除します.
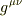 は,
は, 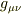 の逆行列なので
の逆行列なので
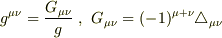 ただし,
ただし, 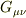 は
は 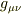 の余因子.
一方,
の余因子.
一方,  を第
を第 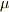 行で展開すると
行で展開すると
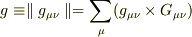 これを
これを 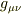 で微分すると,
で微分すると,
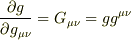 したがって,アインシュタイン規則を復活させて
したがって,アインシュタイン規則を復活させて
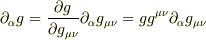 ∴
∴ 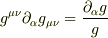 (終)
(終)
#あってるんでしょうか? 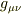 で微分のあたりがあやしいですね.やはりレビ・チビタ使うしかないかも.
#ひとまず,一般には
で微分のあたりがあやしいですね.やはりレビ・チビタ使うしかないかも.
#ひとまず,一般には 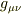 の各成分は独立と考えて問題ないのかな?レビ・チビタで解決する問題でもなさそう.
の各成分は独立と考えて問題ないのかな?レビ・チビタで解決する問題でもなさそう.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/03(Wed) 22:46)
> 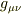 で微分のあたりがあやしいですね.
で微分のあたりがあやしいですね.
「 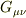 は定義により
は定義により 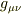 を含まないので,
を含まないので, 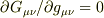 .」
.」
の一文を入れればよいのでは.
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/03(Wed) 22:50)
そうですよね.^^; ありがとうございました.>Hiroさん.
Re: 共変微分による極座標系ラプラシアンの導出
mNeji さんのレス (2008/12/04(Thu) 13:02)
横から失礼します.
傍観者として,大変に興味深く拝見しました.
とくに,このサイトにお邪魔する様になってから,toorisugari no Hiroさんの洗練された解説を何度も見るうちに,「門前の小僧的に目から勉強」させていただいた為に,今回の質疑応答で流れを感じる事ができました.
今後ともに,このような論議の楽しい応酬を拝見したいものです.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/04(Thu) 15:20)
>> 曲率ゼロを仮定するとさらに進みそうな形はしています. > どうなんでしょう.曲率が議論にはいるとおもしろいですが,ラプラシアンは対称なので曲率は出てこない気がします.
曲率が出てしまいました.
結論から書くと
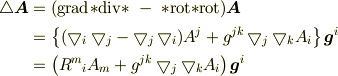
になります. # 一応,内山龍雄「一般相対性理論」p115に,似たような議論が書いてあるので,大はずれではないと思うのですが.
導出は長いですが,
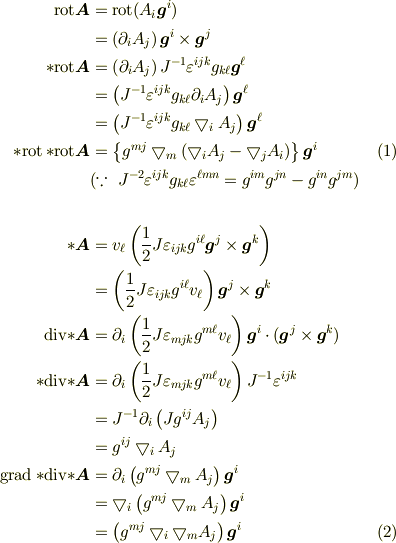
(1)(2)より導出されます.
# ホッジの  双対演算子は,「
双対演算子は,「
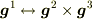 の置き換えをせよ.」という意味で見てください.
の置き換えをせよ.」という意味で見てください.
# 基底を明示的に使う場合でも共変微分は便利なのですね.
# 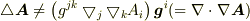 となるのは,「ベクトルラプラシアンはナブラの内積」という解釈が平らな空間でしか成り立たないからでしょうか?
となるのは,「ベクトルラプラシアンはナブラの内積」という解釈が平らな空間でしか成り立たないからでしょうか?
# 結論に出てくる 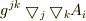 はスカラーラプラシアンではないので,ベクトルラプラシアンを簡略に表記したいという問題は,解決していないままなのですが....
はスカラーラプラシアンではないので,ベクトルラプラシアンを簡略に表記したいという問題は,解決していないままなのですが....
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/04(Thu) 17:04)
> 一般には 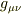 の各成分は独立と考えて問題ないのかな?
の各成分は独立と考えて問題ないのかな?
誤解していたのですが,これは「
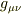 の各成分で独立なのは10個だが,
の各成分で独立なのは10個だが, 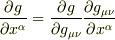 をすべての
をすべての 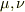 でやって大丈夫か?」
ということでしょうか?
でやって大丈夫か?」
ということでしょうか?
計量の行列式には計量が対称であることは使ってないので,対称性はないとして(自由度10でなく16として)計算して良いのでは?
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/04(Thu) 21:19)
>計量の行列式には計量が対称であることは使ってないので・・・
いやあ,そんなに深く考えたわけでもなく,ただ混乱していたのです. 成分の間に関係があっても,それは「陽に含む」関係ではないので 問題ないですよね.
Re: 共変微分による極座標系ラプラシアンの導出
Yokkun さんのレス (2008/12/04(Thu) 23:47)
今古いテキスト見てて気になったのですが,
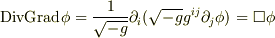
とありました.ということは,一般には
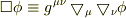 のようです.今考えると
のようです.今考えると  は
は 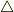 の拡張ですから,当然のような気もします.
の拡張ですから,当然のような気もします.
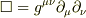 は重力波の議論で限定的に使っているようでした.すみません.
は重力波の議論で限定的に使っているようでした.すみません.
同じテキストに
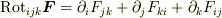 とかあって,Hiroさんのホッジ双対とやらの意味がなんとなくわかりかけてきました.
とかあって,Hiroさんのホッジ双対とやらの意味がなんとなくわかりかけてきました.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/05(Fri) 12:38)
重力波方程式の調和座標系近似の話はしばらくペンディングさせてください.勉強が追いつかない.
> 古いテキスト見てて気になったのですが,
参考までにその文献を教えてください.
Re: 共変微分による極座標系ラプラシアンの導出
toorisugari no Hiro さんのレス (2008/12/05(Fri) 14:49)
> 同じテキストに
> 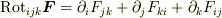 > とかあって,
> とかあって,
4次元空間で
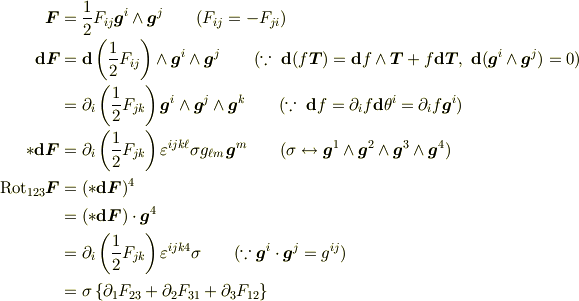
みたいな感じですか?
ホッジ双対を経なくても反対称化
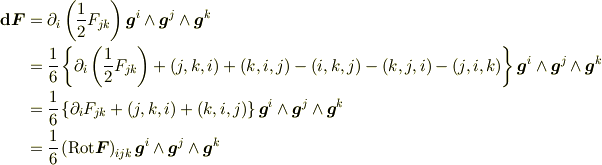
でいいんじゃないかな.
![[\bigtriangledown^2\bm{v}]^i = \bigtriangledown^j \bigtriangledown_j v^i](http://hooktail.maxwell.jp/bbslog/d441c26ad3dca74f712ff6a23555fcaa.png)
![g^{ij}\bigtriangledown_i\bigtriangledown_j v^k = g^{ij}[\partial_i(\bigtriangledown_j v^k)-\Gamma^m_{ij}\bigtriangledown_m v^k+\Gamma^k_{im}\bigtriangledown_j v^m]](http://hooktail.maxwell.jp/bbslog/8a34405eab095f2a5926ea778e6813bb.png)
![= g^{ij}[\partial_i(\partial_j v^k+\Gamma^k_{jm} v^m)-\Gamma^m_{ij}(\partial_m v^k+\Gamma^k_{mn}v^n)+\Gamma^k_{im}(\partial_j v^m+\Gamma^m_{jn}v^n)]](http://hooktail.maxwell.jp/bbslog/4d77c273e4e4d160ab811984185ec704.png)
![g^{ij}\bigtriangledown_i\bigtriangledown_j v^k &= g^{ij}[\partial_i\partial_j v^k+(\partial_i\Gamma^k_{jm}+\Gamma^k_{in}\Gamma^n_{jm})v^m+2\Gamma^k_{im}\partial_j v^m]](http://hooktail.maxwell.jp/bbslog/347d382da52ffcb49cce03349d714165.png)