コイルにかかる電圧と誘導起電力について

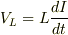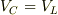この場合，コイルにかかる電圧というのは誘導起電力そのもののことだと思います． $V_L=L\frac{dI}{dt}$ これは，抵抗にかかる電圧が「電圧降下」そのものであることと変わりません．もちろん，一般に V_C = V_L は成り立ちません．電圧の関係は直流と同じで 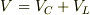V=V_C+V_L ですね．

Re: コイルにかかる電圧と誘導起電力について

うえぽんさんのレス (2008/11/30(Sun) 18:13)

Yokkunさん，ありがとうございます．

もし交流電源にコイルを直接接続した場合は，キルヒホッフの第2法則によって，電源電圧と等量の誘導起電力が生じますよね．だから，コイルに掛かる電圧と誘導起電力の間に直接的な関係があるものだと思い込んでしまっていました．誘導起電力は電流の変化に由来するのであって，コイルに掛かる電圧に由来するものではありませんでしたね…． (交流)電源にコイルを直接接続した場合は，コイルに抵抗が無いものとすると，熱エネルギーとしての損失がないため電流は延々と加速し，すると誘導起電力もどんどん大きくなり，電源電圧と等量になるということでしょうか．この回路の場合も抵抗が無いものとするので，電流は加速すると思うのですが，コンデンサーの極板間電圧が変化するにつれてその加速度も変化するでしょうし，電源電圧も変化するしで，もう訳が分からないことに…．

とりあえず，教科書のコンデンサーとコイルに掛かる電圧が同じという表現は，コンデンサーが電荷を蓄えて生じる電圧と，その電荷の移動によって生じるコイルの誘導起電力が等量であるという理解で良いのでしょうか．つまり，それぞれに掛かる電圧は1/2Vo*sinωtということでしょうか．

Re: コイルにかかる電圧と誘導起電力について

mNeji さんのレス (2008/11/30(Sun) 19:35)

論議を進める前に，共通認識を確認します．

●教科書について

こちらにも，啓林館の物理?，平成19年度用があります．その中で，今回のご質問に近いのは，・第４章電磁誘導と電磁波／第５節電気振動と電磁波と思います．

特に，「抵抗を無視するならば，電流も電圧も同じ」というのに近いのは，「A 電気振動」の「図25 電気振動の実験」についての説明と思います．これはコンデンサとコイルとの自由振動現象の説明と思います．

むしろ，ご質問は，「B共振」の「図27 実験装置」に示されている図をベースに考えられた方が良いと思います．

●私の感触

一応，「第４章電磁誘導と電磁波」は眺めてみましたが，私が高校生とすれば，説明が難しすぎて，困惑してしまいます．

回路の微分方程式に慣れる意味でも，もう少し簡単な例から話を進めた方が良いかも知れません．

何れにしろ，私の説明は長くなりそうなので，Yokkunさんのご説明をお聞きになるのをお勧めします．

Re: コイルにかかる電圧と誘導起電力について

Yokkun さんのレス (2008/11/30(Sun) 19:47)

mNejiさんがおっしゃったように，

>十分に安定した時の振る舞いを考える事にしますが，

に徹した方が無難だと思います．うえぽんさんが前半で考えようとされている考察は「過渡現象」的な考え方で，高校レベルを超えます．コンデンサの充電・放電曲線ぐらいは見たことありますか？この問題ではまして交流電源があるのでやっかいですね．

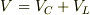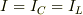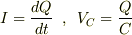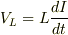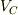基本にかえりましょう．直列だから， (1) V=V_C+V_L (2) I=I_C=I_L また， (3) $I=\frac{dQ}{dt}\,\,\,,\,\,\,V_C=\frac{Q}{C}$ (4) $V_L=L\frac{dI}{dt}$ これらをまとめると，（したがって V_C ）に関する2階微分方程式になります．高校レベルではちょっと難しいかもしれません．電源がないときは単振動の方程式になるのですが，「強制振動」と呼ばれる問題になるのです．

Re: コイルにかかる電圧と誘導起電力について

うえぽんさんのレス (2008/11/30(Sun) 20:42)

丁寧な解説をありがとうございます．2階微分方程式は数学の選択授業で取り扱ったので，ある程度なら理解可能と思います．

が，実は卒業試験を明日に控えておりまして，ちょうど電気振動が試験範囲に含まれているのです．応用的な問題は殆ど出されないので，公式を暗記すれば特に問題は無いのですが，一度突っかかってしまったのでいずれはきちんと理解はしたいと考えております．

議論を展開していただけるというのに失礼な話とは思いますが，今のところは結論だけ教えていただきたく思うのです．なお，試験は今週水曜に終わりますので遅くとも水曜日には再びこの掲示板を確認できるかと思います．

> とりあえず，教科書のコンデンサーとコイルに掛かる電圧が同じという表現は，コンデンサーが電荷を蓄えて生じる電圧と，その電荷の移動によって生じるコイルの誘導起電力が等量であるという理解で良いのでしょうか．つまり，それぞれに掛かる電圧は1/2Vo*sinωtということでしょうか．

これは正しいのでしょうか？

Re: コイルにかかる電圧と誘導起電力について

Yokkun さんのレス (2008/11/30(Sun) 21:33)

もちろん，一般には間違ってますよ．

mNejiさんの >特に，「抵抗を無視するならば，電流も電圧も同じ」というのに近いのは，「A 電気振動」の「図25 電気振動の実験」についての説明と思います．これはコンデンサとコイルとの自由振動現象の説明と思います．

という指摘は検討されたのでしょうか？電源なしの振動回路なら，「抵抗を無視するならば，電流も電圧も同じ」なのは全く初歩的なことです．一方，交流電源がある場合についてそれが一般的に適用できるはずがないではありませんか？

通常交流電源を含む共振回路は高校では扱わないはずですが，授業ではやっているのですか？結論からいえば，振動の因子を 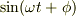$\sin(\omega t+\phi)$ などと仮定して解を求めることになります．

Re: コイルにかかる電圧と誘導起電力について

うえぽんさんのレス (2008/11/30(Sun) 21:50)

> 交流電源がある場合についてそれが一般的に適用できるはずがないではありませんか？何故気づかなかったのか…全くその通りですね．少し混乱していました．

交流電源を含む共振回路の問題は，授業で扱いました．といっても，公式が与えられ，それに代入するだけのものでしたが．

それと，B.共振の説明を読みましたが，実験から次の式が与えられる〜といった説明しかなく，どうしてそうなるのかということまでは書かれていませんでした．

高校生の理解の範囲を超える内容であるなら，今のところは公式を暗記するほか無さそうです．どうもありがとうございました．

Re: コイルにかかる電圧と誘導起電力について

mNeji さんのレス (2008/11/30(Sun) 22:41)

＞交流電源を含む共振回路の問題は，授業で扱いました．といっても，公式が与えられ，それに代入するだけのものでしたが．＞それと，B.共振の説明を読みましたが，実験から次の式が与えられる〜といった説明しかなく，どうしてそうなるのかということまでは書かれていませんでした．

全くその通りです．逆に言えば，高校の教科書の記述はあまりにも抽象的で難しすぎるのです．力学の運動方程式を使わないと，力学の現実が理解出来ないのと同じで，交流回路を云々する前に，簡単な回路，例えば，理想的な電池をコイルと抵抗を直列にしたものに接続したとしての動作を考えたりする必要があると思います．

その意味では；

＃第3節自己誘導と相互誘導＃図９自己誘導の実験＃図１１スイッチを入れたり切ったりした時のコイルを流れる電流と逆起電力

なども，定性的に100回説明するよりも，1回だけでも微分方程式で説明されるほうがイメージが出来易いのだ，と思います．

＞高校生の理解の範囲を超える内容であるなら，今のところは公式を暗記するほか無さそうです．どうもありがとうございました．

試験が終わってから，トライしてみて下さい．

[home] [掲示板] [ページの先頭]