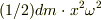慣性モーメント　円柱

home > 掲示板 >

このページのPDF版

サイトマップ

慣性モーメント　円柱

じょけｒさんの書込 (2008/11/27(Thu) 01:21)

授業でわからないところがあるので教えてください．円柱の慣性モーメントで回転軸が重心を通り，底面に並行で側面に垂直な場合についてです．

授業では次のような解法でした

円板の中心を通り円盤に平行な軸に関する慣性モーメントが (1/4)mr^2であることを用いて，平行軸の定理と dm=(M/πhr^2)πr^2 dx であることを用いて，

I=∫[-h/2→h/2](1/4)dm R^2+∫[-h/2→h/2]x^2 dm を計算するというものです

第二項の積分は重心からの距離の二乗と微小な質量の積を足し合わせた物だと理解できますが，第一項で重心における微小な慣性モーメントについても，-h/2からh/2まで足し合わせているところに納得がいきません．

説明をお願いします．読みにくくてすいません．

Re: 慣性モーメント　円柱

Yokkun さんのレス (2008/11/27(Thu) 18:45)

じょけrさん，こんばんは．

実は「平行軸の定理」を微小厚さの円板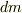に適用すれば，そのまま結果が出てくるのですが，質問の主旨を考えるに実質的に「平行軸の定理」そのものの意味を問われていることになります．

与えられた軸周りの棒の回転において，円板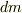がどんな運動をしているかイメージできますか？第1項は自転の慣性，第2項は公転（重心運動）の慣性を表しているのです．「平行軸の定理」自体がこれを示していることがおわかりでしょうか？

Re: 慣性モーメント　円柱

じょけｒさんのレス (2008/11/27(Thu) 22:25)

第一項目が自転，第二項目が公転を表していると言われれば，そんな気もしますが，自分が考えていた平行軸の定理は単に重心からｄ離れた回転軸の周りの慣性モーメントに関するものだと思っていました．なので単に第一項目は重心を通る軸に関する慣性モーメントで第二項目はその重心からｘだけ離れた微小部分に平行軸の定理を適用しながら，足し合わせたものだと理解していました．正直，自転，公転と言われてもピンと来ないのですが，平行軸の定理が理解できていないのでしょうか？

Re: 慣性モーメント　円柱

Yokkun さんのレス (2008/11/27(Thu) 22:34)

質量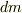の円板が，与えられた軸まわりに（円柱の一部として）角速度 $\omega$ で回転するとき， (1)円板の重心まわりの回転のエネルギー (2)円板の重心運動のエネルギーを考えてみてください．

＃外（慣性系）から見て円板は自転しています．で，自転の角速度は？＃２つの項の和自体が平行軸の定理です．でも定理はわきにおいて，上を考えてみて！＃(1)(2)の「重心」はあくまで円柱ではなく円板の重心です．順序変えました．

Re: 慣性モーメント　円柱

じょけｒさんのレス (2008/11/27(Thu) 23:22)

(1)v=xω E=(1/2)dm v^2=(1/2)dm (xω)^2 ということですか？ (2)の意味がよくわかりません．．．

Re: 慣性モーメント　円柱

Yokkun さんのレス (2008/11/27(Thu) 23:49)

$(1/2) dm \cdot x^2 \omega^2$

これが，重心運動のエネルギーで下記定理の右辺第2項を因子として含みます．で， (1)円板の重心まわりの回転のエネルギーは，下記定理の右辺第1項を因子として含みます．

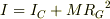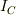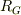平行軸の定理 $I=I_C+{MR_G}^2$ ただし， I_C は重心まわりの慣性モーメント，は剛体の質量， R_G は軸から重心までの距離ですね？

＃多質点系の運動は，重心の運動と重心まわりの相対運動に分解できます．＃お月様は，公転と自転の角速度が同じ．だから，いつでも同じ顔をこちらに向けています．円柱内の円板も同じですね？＃自転の運動エネルギー 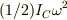$(1/2)I_C\omega^2$ 自転の角運動量 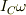$I_C\omega$ 公転の運動エネルギー 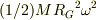$(1/2){MR_G}^2\omega^2$ 公転の角運動量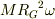 $M{R_G}^2\omega$

Re: 慣性モーメント　円柱

じょけｒさんのレス (2008/11/28(Fri) 00:43)

ありがとうございます．何となくわかった気がします．もう一度よく考えてみます．

Re: 慣性モーメント　円柱

Yokkun さんのレス (2008/11/28(Fri) 08:22)

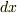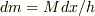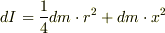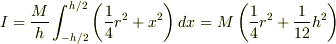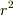座標において円柱を輪切りにして得られる厚さの円板について，質量 dm=Mdx/h として，慣性モーメントは平行軸の定理により $dI = \frac{1}{4}dm\cdot r^2 + dm \cdot x^2$ したがって，円柱全体について積分すれば $I = \frac{M}{h} \int_{-h/2}^{h/2} \left(\frac{1}{4}r^2+x^2\right)dx = M\left(\frac{1}{4}r^2+\frac{1}{12}h^2\right)$ 第1項が r^2 のオーダー，第2項が 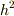h^2 のオーダー．長さに対して太さが無視できない円柱について考えているのですから，第1項を近似で落とすわけにはいきません．