ベクトル解析変形
ベクトル解析変形
すずめ さんの書込 (2008/11/24(Mon) 21:53)
いま電磁気学を勉強しているのですが,どうしても以下の変形[近似]がわかりません.お教えください.
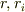 を位置ベクトル,
を位置ベクトル, 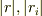 をその位置ベクトルの大きさ,
をその位置ベクトルの大きさ, 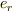 を
を 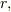 の単位ベクトルとして,
の単位ベクトルとして, 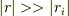 という条件下で,
という条件下で,
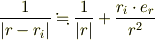
お手数ですがよろしくお願いします.
Re: ベクトル解析変形
Yokkun さんのレス (2008/11/24(Mon) 22:18)
すずめさん,こんばんは.
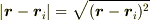 の2乗部分を展開してみましょう.
の2乗部分を展開してみましょう.
あ,あとここではベクトルの斜体太字は,bm{ }が便利なようです. 
Re: ベクトル解析変形
toorisugari no Hiro さんのレス (2008/11/25(Tue) 10:42)
のとき,以下の近似
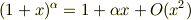
(  は非零の実数.また,
は非零の実数.また, 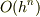 は
は 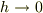 のとき
のとき 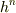 程度で0に近づく数)
が成り立つのをご存じですか?
程度で0に近づく数)
が成り立つのをご存じですか?
Re: ベクトル解析変形
すずめ さんのレス (2008/11/25(Tue) 23:06)
Yokkunさん, toorisugari no Hiroさん,ありがとうございます.
Yokkunさん,
 を展開しますと,
を展開しますと,
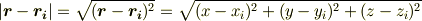
となるのではないでしょうか?
toorisugari no Hiroさん,
はい,存じております.おそらく 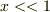 について
について
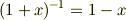
という近似をつかうのでないか,という予想だけはあるのですが, という感じです.
Re: ベクトル解析変形
toorisugari no Hiro さんのレス (2008/11/25(Tue) 23:08)
で,この二つをどう結びつけますか? 考えてみてください.
# 前者は成分を使わない計算が見通しがよいと思います.ヒント: 内積
Re: ベクトル解析変形
すずめ さんのレス (2008/11/25(Tue) 23:21)
toorisugari no Hiroさん,ありがとうございます.
自分で考えると, 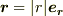 と変形して,
微小量をくくりだすために,
と変形して,
微小量をくくりだすために,
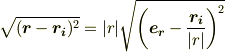
と変形したところで止まります.
Re: ベクトル解析変形
Yokkun さんのレス (2008/11/25(Tue) 23:30)
あ,いい感じですね. 2乗がぬけたのであらためてルートの中2乗しましょう. 展開第2項は内積のままベクトル表示を残してください.
Re: ベクトル解析変形
すずめ さんのレス (2008/11/25(Tue) 23:51)
Yokkunさん
ありがとうございます.ルートの中の2乗は修正しました. ただ,展開第2項というのはどの部分でしょうか?教えてください.
toorisugari no Hiroさん
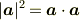
でしょうか?
Re: ベクトル解析変形
toorisugari no Hiro さんのレス (2008/11/26(Wed) 00:11)
もう少し.
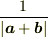 はどう展開できますか?
さらに
はどう展開できますか?
さらに
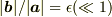 のとき
のとき
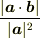 を
を  で評価してください.(ヒント
で評価してください.(ヒント 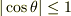 )
)
> 少し混乱してきましたので教えて頂きたいのですが, |b914aeaa237e55ef55395864931ee210| は成立しているのでしょうか?
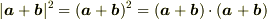 同じ意味です.
同じ意味です.
Re: ベクトル解析変形
Yokkun さんのレス (2008/11/26(Wed) 00:19)
解いている間(?)にちょっとおじゃま.
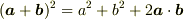 は余弦定理というやつと同じですね.あと,ねまーす.
すずめさん,もう少しですからがんばりましょう.
は余弦定理というやつと同じですね.あと,ねまーす.
すずめさん,もう少しですからがんばりましょう.
Re: ベクトル解析変形
toorisugari no Hiro さんのレス (2008/11/26(Wed) 00:40)
> 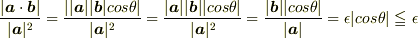 > でしょうか?
> でしょうか?
OK. ふうう.
ではあらためて,問題
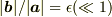 のとき,
のとき, 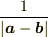 を
を  の一次の精度で近似せよ.ただし,
の一次の精度で近似せよ.ただし, 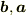 は直交しない(
は直交しない( 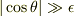 ).
).
# いけるところまで行き詰めてください.たぶん一次式になるはずです.ヒント 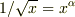
# 前に出した公式少し変更しますね.
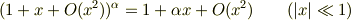
Re: ベクトル解析変形
すずめ さんのレス (2008/11/26(Wed) 01:04)
わかってきました!
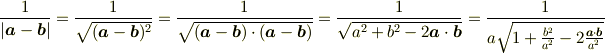
として,近似をつかうんですね...texが混乱してしまい,進まないので 明日また続けさせて下さい.でももういけそうです!ありがとうございます!!
Re: ベクトル解析変形
toorisugari no Hiro さんのレス (2008/11/26(Wed) 01:07)
>わかってきました!
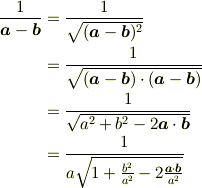
左辺意味不明.
>として,近似をつかって,
> ですか?
-2が消えてる.なのに途中で復活してる何故?
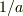 はどこに行った?
はどこに行った?
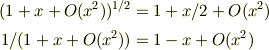
とバラで使っていけば混乱しないと思います.
Re: ベクトル解析変形
すずめ さんのレス (2008/11/27(Thu) 00:40)
遅くなりすみません.texで混乱していました(います).
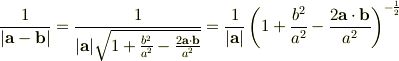
ここで,
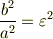
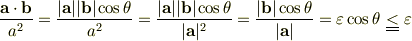
∴
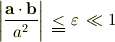
より,近似 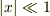 のとき成立する近似
のとき成立する近似
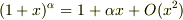 を用いて,
を用いて,
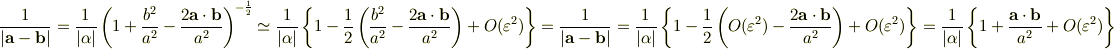
⇔
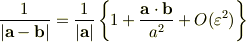
従って,一次の精度で近似しますと,
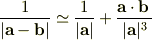
これでどうでしょうか?
Re: ベクトル解析変形
toorisugari no Hiro さんのレス (2008/11/27(Thu) 17:28)
良いと思いますよ. # 最後から2番目の式は長すぎるので途中で改行を入れてください. # TeX中の{}大杉:-) # bfよりbmがよいです.
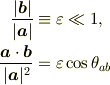
により
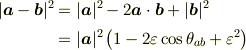
これと,近似式
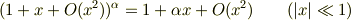
により,
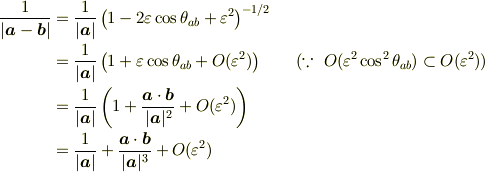
となりますね.
# 得られた関係式
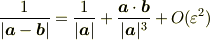
は 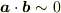 のときでも正しいですが,ランダウの記号を取り除いた近似式
のときでも正しいですが,ランダウの記号を取り除いた近似式
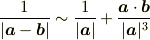
は, 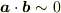 のときには
のときには 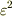 のオーダーの項が優位になり,正当性が怪しくなります.この近似式に対しては,「
のオーダーの項が優位になり,正当性が怪しくなります.この近似式に対しては,「 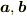 は直交しない(
は直交しない( 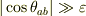 )」という条件を付与した方が安全ですね.
)」という条件を付与した方が安全ですね.
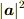 を内積で表現できますか?
を内積で表現できますか?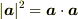 でしょうか?
でしょうか?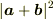 を上の考えに沿って展開してみてください.
を上の考えに沿って展開してみてください.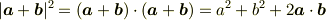
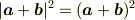
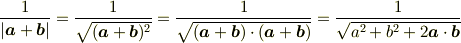
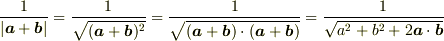 でしょうか?
でしょうか?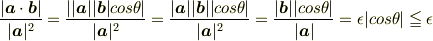
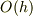 は
は 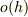 とは別物
とは別物